1 1/7 As A Decimal
plugunplug
Sep 25, 2025 · 5 min read
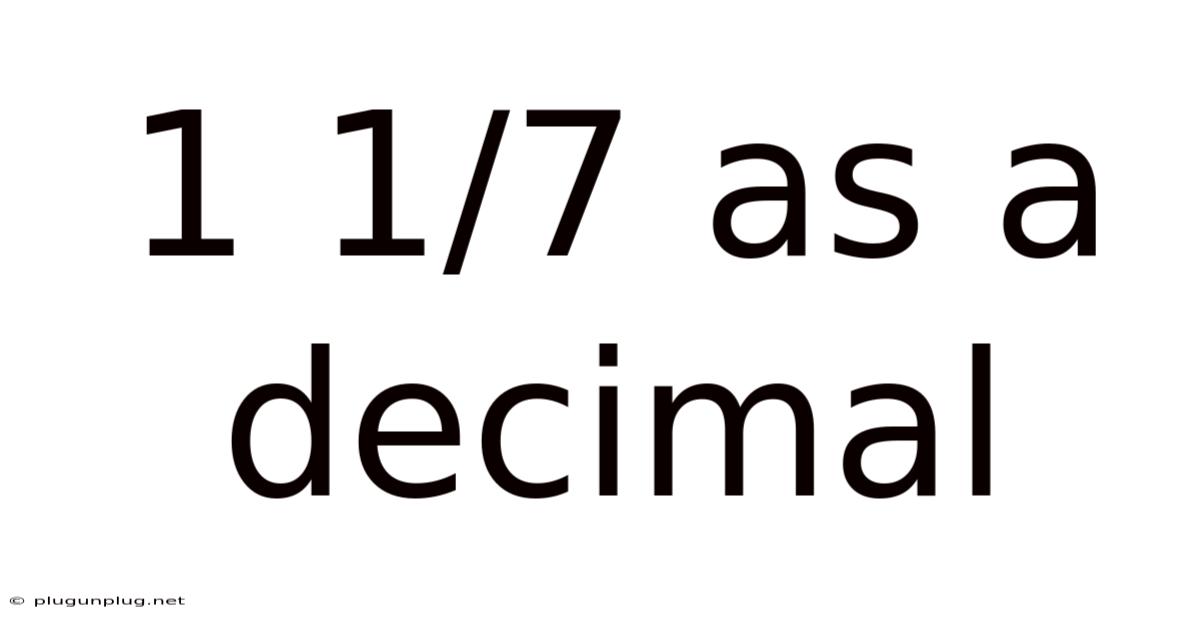
Table of Contents
Decoding 1 1/7 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article delves deep into the process of converting the mixed number 1 1/7 into its decimal equivalent, exploring the underlying principles and providing a step-by-step guide. We'll also address common misconceptions and answer frequently asked questions, making this a comprehensive resource for anyone seeking a thorough understanding of this mathematical concept.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's clarify the terms. A mixed number combines a whole number and a fraction, like 1 1/7. A decimal represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part (e.g., 1.142857). Converting a mixed number to a decimal involves expressing the fractional part as a decimal and then adding it to the whole number part.
Step-by-Step Conversion of 1 1/7 to Decimal
The conversion of 1 1/7 to a decimal involves two primary steps:
1. Converting the Fraction to a Decimal:
The core of the conversion lies in transforming the fraction 1/7 into its decimal representation. This is achieved through division. We divide the numerator (1) by the denominator (7):
1 ÷ 7 = 0.142857142857...
Notice the repeating pattern: 142857. This indicates a repeating decimal, also known as a recurring decimal. The sequence "142857" repeats infinitely.
2. Adding the Whole Number:
Now, we simply add the whole number part (1) to the decimal representation of the fraction (0.142857142857...):
1 + 0.142857142857... = 1.142857142857...
Therefore, 1 1/7 as a decimal is approximately 1.142857. We use "approximately" because the decimal representation is infinite. For practical purposes, we often round the decimal to a specific number of decimal places. Rounding to four decimal places, we get 1.1429.
Understanding Repeating Decimals
The repeating decimal nature of 1/7 is a key characteristic. It's not a coincidence; certain fractions, especially those with denominators that are not factors of powers of 10 (2 and 5), result in repeating decimals. The length of the repeating sequence varies depending on the denominator. For instance, 1/3 = 0.333..., while 1/7 has a longer repeating sequence (142857).
The repeating decimal 0.142857... can be represented using a bar notation: 0.$\overline{142857}$. The bar above the digits indicates the repeating sequence. This notation is more concise and accurately represents the infinite nature of the decimal.
Different Methods for Conversion
While long division is the most straightforward method, alternative approaches exist, particularly for those comfortable with algebraic manipulation. However, for a mixed number as simple as 1 1/7, long division remains the most efficient and readily understandable approach.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is vital in many areas:
- Everyday Calculations: Dividing a pizza amongst friends, calculating discounts, or sharing costs.
- Scientific Calculations: In physics, chemistry, and engineering, precise calculations often require decimal representations.
- Computer Programming: Many programming languages rely on decimal representations for numerical operations.
- Financial Calculations: Interest calculations, currency conversions, and profit margins frequently involve decimal manipulation.
- Measurement and Engineering: Representing precise measurements, particularly in metric systems.
Addressing Common Misconceptions
Several common misconceptions surround decimal conversions:
- Rounding Errors: When rounding repeating decimals, it's crucial to understand that you are introducing a small degree of error. The more decimal places you retain, the smaller the error becomes.
- Terminating vs. Repeating Decimals: Not all fractions result in repeating decimals. Fractions with denominators that are only factors of 2 and 5 (or combinations thereof) will result in terminating decimals (decimals that end). For example, 1/2 = 0.5, and 1/10 = 0.1.
- The Importance of Precision: Depending on the application, the level of precision required for the decimal representation varies significantly. In some cases, a rough approximation is sufficient, while in others, high precision is crucial.
Frequently Asked Questions (FAQ)
Q: Can 1 1/7 be expressed as a perfect decimal?
A: No. 1 1/7 results in a repeating decimal; it cannot be expressed as a finite decimal without introducing rounding errors.
Q: How many decimal places should I use when representing 1 1/7 as a decimal?
A: The appropriate number of decimal places depends on the context. For most everyday purposes, four decimal places (1.1429) offer sufficient accuracy. For scientific or engineering applications, more decimal places may be necessary.
Q: What if the mixed number had a larger fraction, say 17/23? Would the process be the same?
A: Yes, the process remains the same. You would divide the numerator (17) by the denominator (23) to obtain the decimal representation of the fraction, then add the whole number part (1). The result might be a longer repeating decimal or even a terminating decimal, depending on the fraction.
Conclusion: Mastering Decimal Conversions
Converting fractions, including mixed numbers like 1 1/7, to decimals is a valuable skill with broad applicability. Understanding the process, recognizing the nature of repeating decimals, and applying appropriate rounding techniques are crucial for accuracy and effective problem-solving in diverse mathematical contexts. While seemingly simple, mastering decimal conversions forms a solid foundation for more advanced mathematical concepts and applications across various disciplines. Remember to choose the level of precision that suits your specific needs, keeping in mind the potential for rounding errors when dealing with repeating decimals. The more you practice, the more comfortable and proficient you will become in handling these conversions.
Latest Posts
Latest Posts
-
What Do Hammer Sharks Eat
Sep 25, 2025
-
Octagon Is How Many Sides
Sep 25, 2025
-
Lady Macbeth And Macbeth Relationship
Sep 25, 2025
-
Name Of The Thigh Muscle
Sep 25, 2025
-
Animals In Temperate Coniferous Forest
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 1 1/7 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.