1 2 3 X 3
plugunplug
Sep 17, 2025 · 6 min read
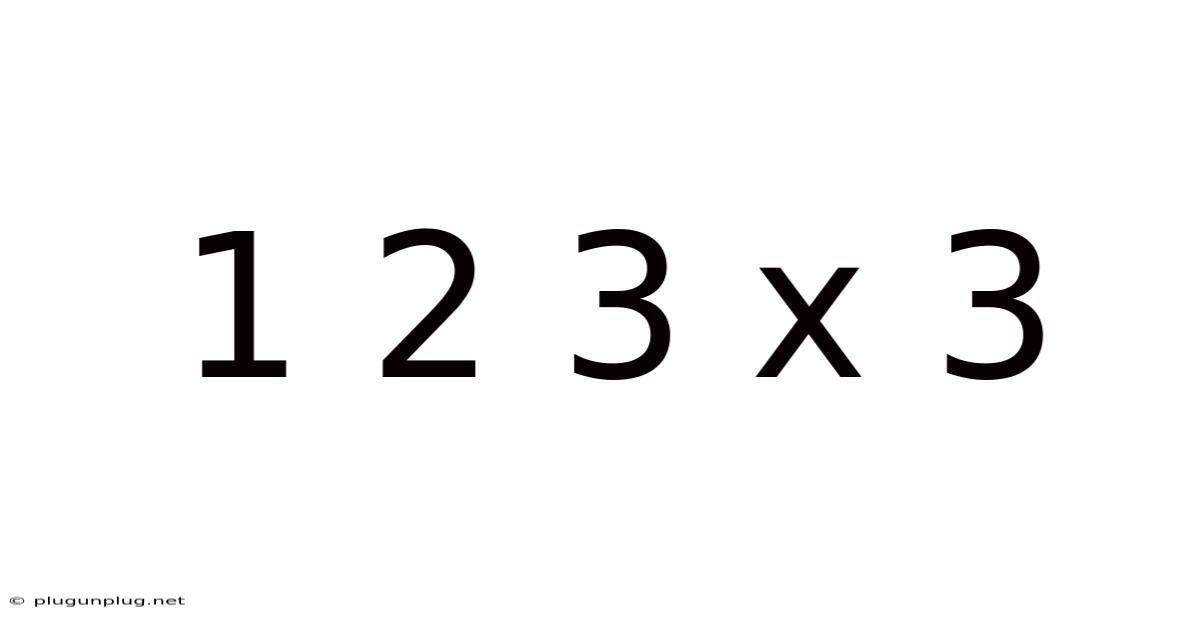
Table of Contents
Decoding 1 2 3 x 3: Exploring the Multiplicative World of Simple Arrays
This article delves into the seemingly simple yet surprisingly rich mathematical concept represented by "1 2 3 x 3". We'll move beyond the basic arithmetic to explore its applications in various fields, from elementary mathematics to advanced concepts like matrices and arrays in computer science. Understanding this seemingly simple multiplication problem unlocks a gateway to a deeper understanding of fundamental mathematical principles and their practical applications. This exploration will be accessible to individuals of various mathematical backgrounds, ensuring that even those with limited prior knowledge can grasp the core concepts.
Introduction: Beyond Basic Multiplication
At first glance, "1 2 3 x 3" appears as a straightforward multiplication problem. We simply multiply each number in the sequence (1, 2, and 3) by 3, resulting in the sequence (3, 6, and 9). However, this simple arithmetic operation opens doors to a much broader understanding of mathematical structures and their practical uses. The expression can be interpreted in several ways, depending on the context. It can represent a simple scalar multiplication, the foundation for understanding matrix operations, or even an array manipulation in programming. This article will explore these interpretations systematically.
Understanding Scalar Multiplication
In its simplest form, "1 2 3 x 3" represents scalar multiplication. Scalar multiplication involves multiplying a vector (or a sequence of numbers) by a single number (the scalar). In this case, the vector is (1, 2, 3), and the scalar is 3. The resulting vector is (3, 6, 9), obtained by multiplying each element of the original vector by the scalar. This fundamental concept is crucial in linear algebra and has far-reaching implications in physics, engineering, and computer graphics.
Scalar Multiplication in Linear Algebra
Linear algebra heavily relies on scalar multiplication. Vectors, which represent quantities with both magnitude and direction, are frequently manipulated using scalar multiplication. This operation scales the vector, changing its magnitude but not its direction. For example, if (1, 2, 3) represents a force vector, multiplying it by 3 triples the force's magnitude while maintaining its direction.
Scalar Multiplication in Computer Graphics
In computer graphics, scalar multiplication is essential for transformations like scaling. To enlarge an object, we multiply the coordinates of its vertices by a scalar greater than 1. Conversely, to shrink the object, we use a scalar between 0 and 1. This simple operation forms the bedrock of many complex graphical manipulations.
Exploring the Concept of Arrays
The expression "1 2 3 x 3" can also be viewed as an operation on an array. An array is a data structure in computer science that stores a collection of elements of the same data type. In this context, (1, 2, 3) can be considered a one-dimensional array. Multiplying this array by 3 involves multiplying each element of the array by 3, resulting in a new array (3, 6, 9). This concept is fundamental in many programming languages and is used extensively in various applications.
Array Operations in Programming
Arrays are fundamental in programming, providing efficient ways to store and manipulate data. They are used in countless applications, from simple data processing to complex algorithms in machine learning. The operation of multiplying each element of an array by a scalar (like in our example) is a basic yet powerful operation that underpins many more complex algorithms.
Array Operations and Efficiency
Working with arrays directly rather than individual variables improves code efficiency. Many programming languages offer optimized functions for array operations, making computations significantly faster than working with each element separately. This efficiency becomes particularly crucial when dealing with large datasets.
Matrices and Matrix Multiplication: A Deeper Dive
While the simple multiplication we’ve discussed so far is fundamental, let's delve into a slightly more complex yet closely related concept: matrices. A matrix is a two-dimensional array of numbers. While "1 2 3 x 3" doesn't directly represent matrix multiplication in its simplest form, it lays the groundwork for understanding it. Let's consider how this concept would extend to matrices.
Imagine we have a 1x3 matrix (a row matrix): [1 2 3]. Multiplying this matrix by the scalar 3 results in [3 6 9]. This is a direct application of scalar multiplication to a matrix.
True matrix multiplication requires two matrices with compatible dimensions. To multiply a matrix by another, the number of columns in the first matrix must equal the number of rows in the second. While our example doesn't directly illustrate this, it lays the conceptual groundwork. Understanding scalar multiplication is a crucial prerequisite to grasping matrix multiplication.
Matrix Multiplication in Linear Algebra and Beyond
Matrix multiplication has extensive applications in linear algebra, computer graphics, and machine learning. It's used to represent linear transformations, solve systems of linear equations, and perform complex calculations efficiently. The operations involved in matrix multiplication build upon the basic scalar multiplication we explored earlier.
Applications of Matrices
- Linear Transformations: Matrices are instrumental in representing linear transformations such as rotations, scaling, and shearing in computer graphics.
- System of Equations: Solving systems of linear equations can be greatly simplified using matrix operations.
- Machine Learning: Matrix operations are the cornerstone of many machine learning algorithms, particularly in areas like deep learning.
Practical Applications: Real-World Examples
The principles underlying "1 2 3 x 3" extend far beyond simple arithmetic. Let's look at some real-world applications:
- Scaling in Computer-Aided Design (CAD): In CAD software, designers frequently scale objects. This involves multiplying the coordinates of the object's vertices by a scalar value, exactly as we described with scalar multiplication.
- Signal Processing: In signal processing, scalar multiplication is used to adjust the amplitude of signals. This is crucial in audio processing and telecommunications.
- Physics: Vectors representing forces, velocities, or accelerations are often scaled using scalar multiplication. For example, doubling the velocity of an object is simply scalar multiplication by 2.
Frequently Asked Questions (FAQ)
Q: Is "1 2 3 x 3" the same as (1 x 3) (2 x 3) (3 x 3)?
A: Yes, in the context of scalar multiplication or array operations, it is equivalent. Each element in the sequence (1, 2, 3) is multiplied by 3 individually.
Q: What if the 'x 3' was replaced with another number?
A: The principle remains the same. The number would act as a scalar, multiplying each element of the sequence (1, 2, 3).
Q: How does this relate to more advanced mathematical concepts?
A: The basic principles of scalar multiplication and array operations are fundamental building blocks for understanding more advanced concepts like matrix multiplication, linear transformations, and tensor operations in machine learning.
Q: Can I apply this to other sequences of numbers?
A: Absolutely! The principle applies to any sequence of numbers. You can replace (1, 2, 3) with any other sequence and multiply each element by the scalar.
Conclusion: The Power of Simplicity
The seemingly simple expression "1 2 3 x 3" provides a powerful entry point into a vast landscape of mathematical concepts and their real-world applications. By understanding scalar multiplication, array operations, and the foundational principles of matrix algebra, we can appreciate the broad implications of this seemingly straightforward arithmetic problem. This exploration highlights the importance of understanding even the simplest mathematical operations, as they often form the basis for more complex and powerful tools used across diverse fields. The ability to grasp these fundamental concepts is crucial for success in various STEM fields and beyond. This exploration encourages further investigation into the rich world of mathematics, where simplicity often belies profound depth and far-reaching applicability.
Latest Posts
Latest Posts
-
What Is Penetration Pricing Strategy
Sep 17, 2025
-
Bubble Skin Care For Kids
Sep 17, 2025
-
All The Factors For 26
Sep 17, 2025
-
Bond Angle Of Trigonal Pyramidal
Sep 17, 2025
-
What Were The Four Humours
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 2 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.