1/2 X 1/2 X 1/4
plugunplug
Sep 22, 2025 · 6 min read
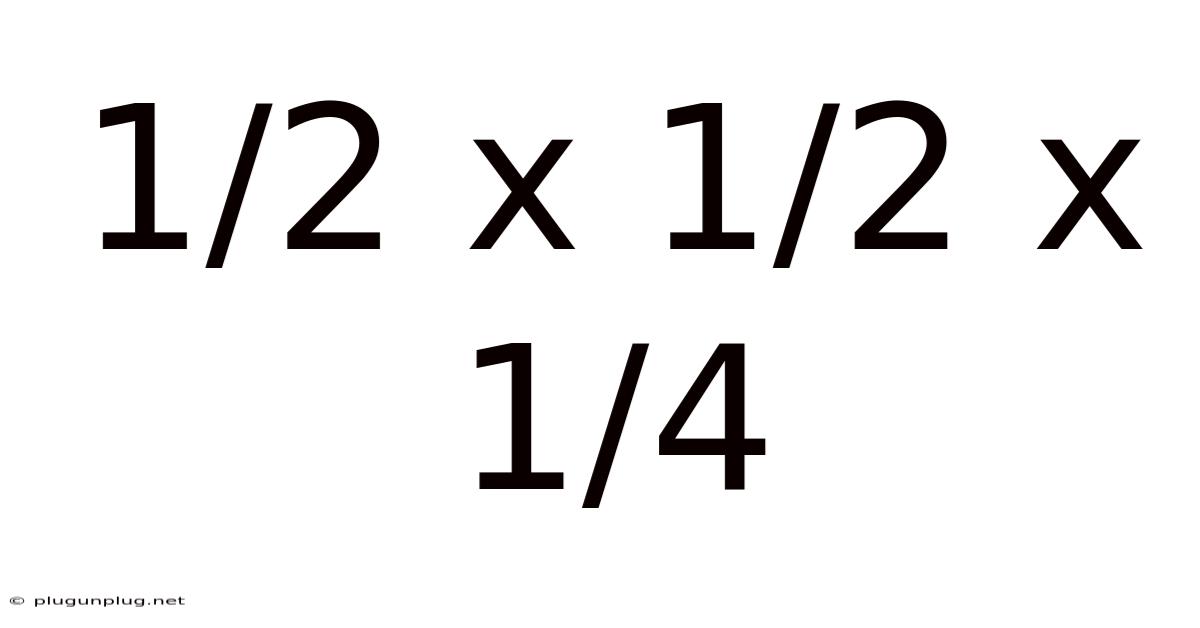
Table of Contents
Decoding 1/2 x 1/2 x 1/4: A Deep Dive into Fraction Multiplication
This article explores the seemingly simple calculation of 1/2 x 1/2 x 1/4, delving beyond the basic arithmetic to understand the underlying concepts of fraction multiplication, its practical applications, and its relevance in various fields. We'll break down the process step-by-step, explore the mathematical principles involved, and address common misconceptions. This comprehensive guide is perfect for anyone looking to solidify their understanding of fractions and their applications in everyday life and advanced studies.
Understanding Fraction Multiplication: The Basics
Before diving into the specific calculation of 1/2 x 1/2 x 1/4, let's review the fundamental principles of multiplying fractions. Multiplying fractions is, in essence, a process of finding a portion of a portion. Each fraction represents a part of a whole. When we multiply fractions, we are essentially finding a fraction of another fraction.
The process is straightforward:
-
Multiply the numerators: The numerators are the top numbers in the fractions. Multiply them together to get the numerator of the resulting fraction.
-
Multiply the denominators: The denominators are the bottom numbers in the fractions. Multiply them together to get the denominator of the resulting fraction.
-
Simplify (reduce) the resulting fraction: If possible, simplify the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
For example, let's consider a simpler multiplication: 1/3 x 2/5.
- Multiply the numerators: 1 x 2 = 2
- Multiply the denominators: 3 x 5 = 15
- The resulting fraction is 2/15. Since 2 and 15 have no common divisors other than 1, the fraction is already in its simplest form.
Solving 1/2 x 1/2 x 1/4: A Step-by-Step Approach
Now, let's apply these principles to our target calculation: 1/2 x 1/2 x 1/4.
-
Multiply the numerators: 1 x 1 x 1 = 1
-
Multiply the denominators: 2 x 2 x 4 = 16
-
The resulting fraction is 1/16. The numerator (1) and the denominator (16) have no common divisors other than 1, so the fraction is already simplified.
Therefore, 1/2 x 1/2 x 1/4 = 1/16.
Visualizing Fraction Multiplication: A Geometric Approach
Understanding fraction multiplication can be greatly enhanced by visualizing it geometrically. Imagine a square representing the whole (1).
-
1/2 x 1/2: Dividing the square in half horizontally and then in half vertically creates four smaller squares. Each smaller square represents 1/4 of the original square. This visually demonstrates that 1/2 x 1/2 = 1/4.
-
1/2 x 1/2 x 1/4: Taking the 1/4 from the previous step, imagine dividing each of those four squares into four even smaller squares. This creates a total of 16 smaller squares. Each of these smallest squares represents 1/16 of the original square. This visually confirms that 1/2 x 1/2 x 1/4 = 1/16.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it has numerous practical applications in daily life and various professional fields:
-
Cooking and Baking: Scaling recipes up or down often involves multiplying fractions. If a recipe calls for 1/2 cup of flour and you want to make half the recipe, you'll need to calculate 1/2 x 1/2 = 1/4 cup of flour.
-
Construction and Engineering: Calculating material quantities, determining precise measurements, and scaling blueprints all rely heavily on fraction multiplication. For instance, calculating the volume of a rectangular prism might involve multiplying fractional dimensions.
-
Finance and Accounting: Calculating percentages, interest rates, and proportions of investments involves frequent use of fraction multiplication.
-
Data Analysis and Statistics: Understanding proportions and probabilities often requires multiplying fractions to determine the likelihood of specific events.
-
Science and Physics: Many scientific formulas and calculations involve multiplying fractions to represent ratios and proportions.
Beyond the Basics: Understanding the Commutative and Associative Properties
Fraction multiplication, like other forms of multiplication, obeys the commutative and associative properties:
-
Commutative Property: The order in which you multiply fractions doesn't affect the result. 1/2 x 1/2 x 1/4 is the same as 1/4 x 1/2 x 1/2, or any other permutation.
-
Associative Property: You can group the fractions in different ways without altering the outcome. (1/2 x 1/2) x 1/4 is equal to 1/2 x (1/2 x 1/4).
Addressing Common Misconceptions
Several common misconceptions surround fraction multiplication:
-
Adding instead of multiplying: A frequent mistake is adding the numerators and adding the denominators instead of multiplying them. Remember, multiplying fractions is fundamentally different from adding them.
-
Incorrect simplification: Failing to simplify the resulting fraction to its lowest terms is another common error. Always check if the numerator and denominator share a common divisor greater than 1.
-
Difficulty visualizing fractions: Many struggle to visualize fractions and their multiplication. Using geometric representations or real-world analogies can significantly aid understanding.
Expanding on the Concept: Multiplying More Than Three Fractions
The principles we've discussed extend seamlessly to multiplying more than three fractions. The procedure remains the same:
- Multiply all the numerators together.
- Multiply all the denominators together.
- Simplify the resulting fraction.
For example, 1/2 x 1/3 x 1/4 x 1/5:
- Numerators: 1 x 1 x 1 x 1 = 1
- Denominators: 2 x 3 x 4 x 5 = 120
- Result: 1/120
Frequently Asked Questions (FAQ)
Q: Can I multiply fractions with different denominators?
A: Yes, absolutely. The procedure for multiplying fractions remains the same regardless of whether the denominators are the same or different.
Q: What if one of the fractions is a whole number?
A: Treat the whole number as a fraction with a denominator of 1. For example, 2 x 1/4 is the same as 2/1 x 1/4 = 2/4 = 1/2.
Q: What is the significance of simplifying fractions?
A: Simplifying fractions is crucial for presenting the result in its most concise and understandable form. It also helps in subsequent calculations and comparisons.
Q: Are there any shortcuts for multiplying fractions?
A: While there aren't significant shortcuts for the core process, you can sometimes simplify before multiplying by canceling common factors between numerators and denominators. For example, in 2/4 x 1/2, you can simplify 2/4 to 1/2 before multiplying, resulting in 1/2 x 1/2 = 1/4.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a fundamental skill with far-reaching applications. Understanding the underlying principles, visualizing the process, and practicing regularly will build confidence and proficiency. While the calculation of 1/2 x 1/2 x 1/4 might seem simple at first glance, it serves as a gateway to understanding more complex fraction manipulations and their importance in diverse fields. This comprehensive exploration has hopefully illuminated not only the solution but also the broader mathematical concepts and practical applications surrounding this seemingly straightforward calculation. Remember to practice regularly and use different approaches—visual, numerical, and real-world examples—to solidify your understanding.
Latest Posts
Latest Posts
-
What Is 66f In Celsius
Sep 22, 2025
-
Triangle Inscribed In A Circle
Sep 22, 2025
-
What Light Yonder Window Breaks
Sep 22, 2025
-
Socialism With A Human Face
Sep 22, 2025
-
Meaning Of The Prefix Inter
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1/2 X 1/2 X 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.