1 25 As A Percent
plugunplug
Sep 16, 2025 · 5 min read
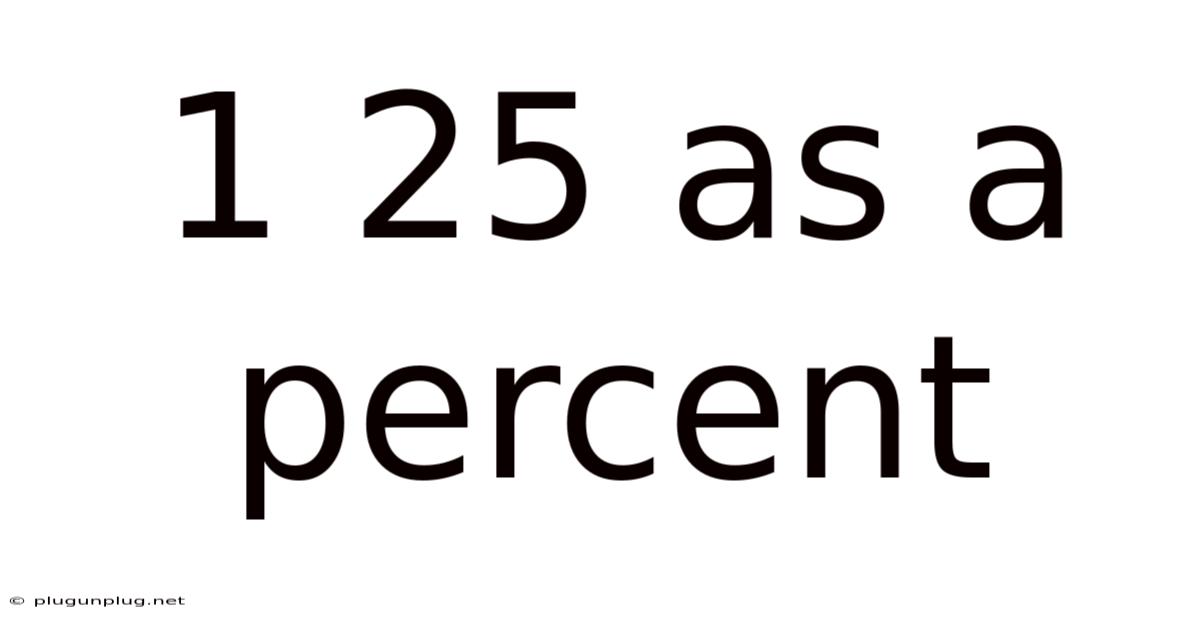
Table of Contents
Understanding 1/25 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This article will delve into the conversion of the fraction 1/25 into a percentage, providing a detailed explanation suitable for learners of all levels. We'll explore various methods for this conversion, explain the underlying mathematical principles, and offer practical examples to solidify your understanding. This guide aims to not just provide the answer but also build a robust conceptual foundation for working with fractions and percentages.
What is a Percentage?
Before we dive into converting 1/25, let's clarify the concept of a percentage. A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50%, for example, represents 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental definition is crucial for converting fractions to percentages and vice versa.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 1/25 into a percentage involves two simple steps:
-
Convert the fraction to a decimal: To do this, we divide the numerator (1) by the denominator (25). 1 ÷ 25 = 0.04
-
Convert the decimal to a percentage: To express a decimal as a percentage, we multiply it by 100 and add the "%" symbol. 0.04 x 100 = 4%.
Therefore, 1/25 is equal to 4%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the definition of percentage as a fraction out of 100. We aim to find an equivalent fraction to 1/25 that has a denominator of 100.
To achieve this, we ask ourselves: "What number, when multiplied by 25, equals 100?" The answer is 4 (25 x 4 = 100).
Since we multiply the denominator by 4, we must also multiply the numerator by 4 to maintain the equivalence of the fraction. Thus:
1/25 x 4/4 = 4/100
Since 4/100 represents 4 out of 100, it is equivalent to 4%. This method clearly illustrates the meaning of percentage as a fraction of 100.
Method 3: Using Proportions
Proportions offer another elegant way to solve this conversion. We can set up a proportion where x represents the percentage we want to find:
1/25 = x/100
To solve for x, we cross-multiply:
25x = 100
x = 100/25
x = 4
Therefore, 1/25 is equivalent to 4%. This method emphasizes the relationship between the fraction and its percentage equivalent.
Understanding the Mathematical Principles
The core concept underlying these methods is the equivalence of fractions. We manipulate fractions to express them in different forms while maintaining their numerical value. Converting to a decimal involves division, while converting to a percentage involves multiplication by 100. These operations are fundamental to working with fractions and percentages. The concept of proportionality highlights the consistent relationship between the fraction and its percentage representation.
Practical Applications of 1/25 as a Percent
The knowledge that 1/25 equals 4% has numerous practical applications:
-
Discounts: A 4% discount on an item is equivalent to a reduction of 1/25 of its original price.
-
Taxes: A 4% sales tax represents an additional cost of 1/25 of the item's price.
-
Financial Analysis: Understanding percentage changes in financial statements often involves working with fractions that need conversion into percentages.
-
Statistics: Expressing proportions and probabilities often involves translating fractions into percentages for easier interpretation.
-
Everyday Calculations: Many daily calculations, from calculating tips to understanding survey results, benefit from understanding fractional percentages.
Expanding the Understanding: Working with Other Fractions
The methods used to convert 1/25 to a percentage can be applied to other fractions. The key steps remain consistent:
-
Divide the numerator by the denominator to get a decimal.
-
Multiply the decimal by 100 to obtain the percentage.
For example, let's convert 3/5 to a percentage:
-
3 ÷ 5 = 0.6
-
0.6 x 100 = 60%
Therefore, 3/5 is equal to 60%.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, absolutely! Any fraction can be converted to a percentage using the methods described above.
Q: What if the resulting decimal is very long?
A: You can round the decimal to a reasonable number of decimal places before converting it to a percentage. The level of precision required depends on the context of the problem.
Q: Is there a quick way to convert fractions to percentages?
A: For some common fractions, memorizing their percentage equivalents can be helpful (e.g., 1/2 = 50%, 1/4 = 25%, 1/10 = 10%). However, the methods discussed above provide a general approach for any fraction.
Q: Why is understanding percentages important?
A: Percentages provide a standardized and readily understandable way to compare proportions and fractions. Their use is pervasive in various fields, making them an essential part of mathematical literacy.
Conclusion
Converting 1/25 to a percentage, resulting in 4%, is a straightforward yet fundamental skill in mathematics. By understanding the methods of direct conversion, equivalent fractions, and proportions, you can confidently perform this conversion and apply it to a wide range of practical scenarios. Mastering this concept forms a strong foundation for further exploration of fractions, decimals, and percentages, which are essential tools in numerous academic and real-world applications. This comprehensive guide not only provides the answer but also aims to build a thorough understanding of the underlying mathematical principles, equipping you with the skills to tackle similar conversions with ease. Remember that consistent practice is key to mastering these concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.