1 4 X 3 4
plugunplug
Sep 25, 2025 · 6 min read
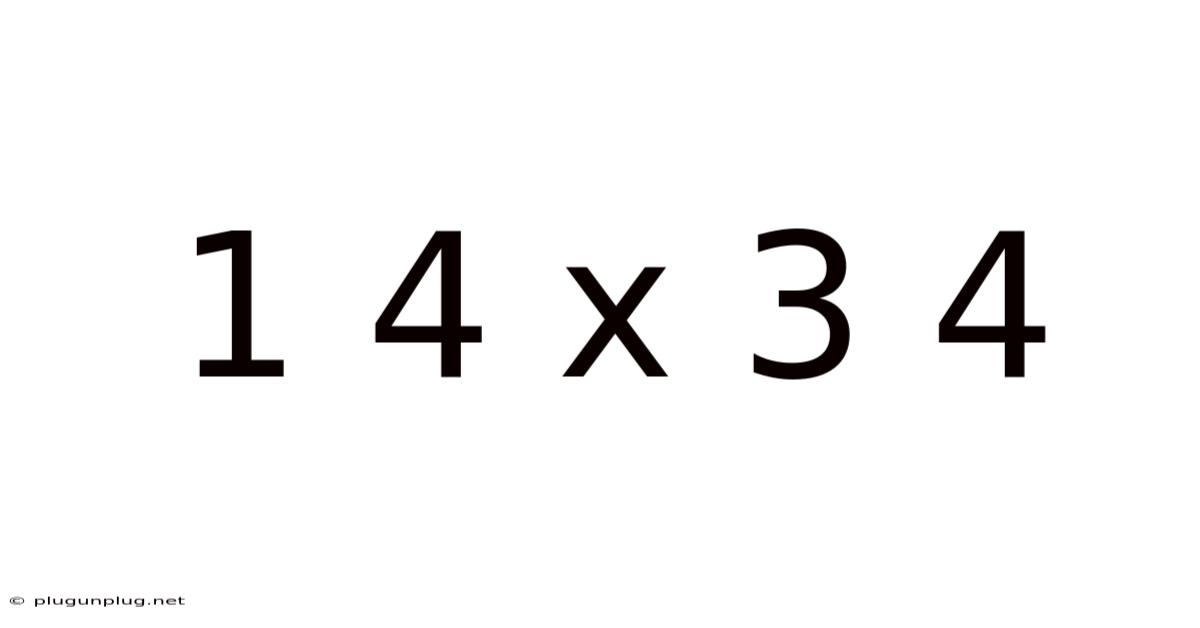
Table of Contents
Decoding the Mystery: Understanding 1 ¼ x 3 ¼ and its Applications
This article delves into the seemingly simple yet surprisingly multifaceted world of the fraction 1 ¼ x 3 ¼. We'll explore its mathematical significance, practical applications across various fields, and how to effectively utilize this measurement in real-world scenarios. Understanding this seemingly basic concept opens doors to a deeper appreciation of fractions, geometry, and even the design principles behind everyday objects.
Introduction: More Than Just Numbers
At first glance, 1 ¼ x 3 ¼ might seem like just a pair of mixed numbers. However, these numbers represent a specific measurement, often expressed in inches or centimeters, that holds significant importance in various fields, from carpentry and construction to crafting and design. This article will unpack the meaning behind these numbers, exploring how they are used and the mathematical concepts that underpin their application. We will also address common misunderstandings and provide practical examples to solidify your understanding.
Understanding the Components: Mixed Numbers and Fractions
Before delving into the calculations and applications of 1 ¼ x 3 ¼, let’s solidify our understanding of its components: mixed numbers and fractions.
-
Mixed Numbers: A mixed number combines a whole number and a proper fraction. For example, 1 ¼ means one whole unit and one-quarter of another unit. Understanding this structure is key to performing calculations with mixed numbers.
-
Proper Fractions: A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). In 1 ¼, ¼ is a proper fraction, indicating a part of a whole.
-
Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. While we are working with mixed numbers in this instance, converting to improper fractions is often a crucial step in performing calculations. To convert 1 ¼ to an improper fraction, we multiply the whole number (1) by the denominator (4) and add the numerator (1), placing the result over the original denominator: (1 x 4) + 1 = 5/4.
Calculating the Area: Practical Applications of 1 ¼ x 3 ¼
One of the most common applications of 1 ¼ x 3 ¼ involves calculating the area of a rectangle or square. This measurement could represent the dimensions of a piece of wood, a canvas, a tile, or any other rectangular object.
To calculate the area, we simply multiply the length by the width:
1 ¼ x 3 ¼ = ?
First, let's convert the mixed numbers into improper fractions:
1 ¼ = 5/4 3 ¼ = 13/4
Now, we multiply the improper fractions:
(5/4) x (13/4) = 65/16
This result, 65/16, is an improper fraction. To express it as a mixed number, we perform a division:
65 ÷ 16 = 4 with a remainder of 1
Therefore, the area is 4 ⅛ square units. If the units are inches, the area is 4 ⅛ square inches.
Beyond Area Calculation: Exploring Other Applications
While area calculation is a prevalent application, 1 ¼ x 3 ¼ finds its way into various other contexts:
-
Construction and Carpentry: This measurement could represent the dimensions of a specific component in a larger project. Accurate measurements are crucial for a well-fitting and functional structure. Understanding how to work with fractions in this context is essential for success.
-
Crafting and DIY Projects: Whether you are creating a piece of artwork, constructing a piece of furniture, or working on a sewing project, precise measurements are vital for achieving the desired outcome. The ability to work with fractions ensures accuracy and prevents errors that could compromise the final product.
-
Baking and Cooking: Recipes sometimes use fractional measurements for ingredients. Understanding how to interpret and work with these fractions is crucial for achieving the correct consistency and taste in the final dish.
-
Scale Models and Design: In architecture, engineering, and other design fields, understanding scale is crucial. A measurement of 1 ¼ x 3 ¼ might represent a scaled-down version of a larger object.
Addressing Common Mistakes and Misconceptions
Several common mistakes can arise when working with fractions, especially mixed numbers:
-
Incorrect Conversion to Improper Fractions: Failure to accurately convert mixed numbers to improper fractions before performing calculations can lead to incorrect results. It's essential to master this conversion process.
-
Mistakes in Multiplication of Fractions: Forgetting to multiply both the numerators and the denominators separately can lead to errors. Remember, (a/b) x (c/d) = (a x c) / (b x d).
-
Incorrect Simplification of Fractions: After multiplying fractions, it's crucial to simplify the result to its lowest terms. This involves dividing both the numerator and the denominator by their greatest common divisor.
-
Misinterpreting the Units: Always pay close attention to the units of measurement (inches, centimeters, etc.). Failing to do so can lead to errors in the final answer.
Further Exploration: Expanding Mathematical Knowledge
Understanding 1 ¼ x 3 ¼ opens a pathway to more complex mathematical concepts:
-
Decimal Conversions: Converting fractions to decimals and vice versa is a crucial skill. 1 ¼ is equivalent to 1.25, and 3 ¼ is equivalent to 3.25. Understanding this equivalence enables the use of calculators and other decimal-based tools for calculations.
-
Algebraic Equations: The principles of working with fractions extend to algebraic equations, where fractions are often used to represent unknown variables.
-
Geometry and Trigonometry: The understanding of fractions is fundamental to various geometric calculations, particularly those involving area, volume, and angles.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve 1 ¼ x 3 ¼? A: Yes, you can. However, it's essential to convert the mixed numbers to decimals (1.25 x 3.25) before using the calculator.
-
Q: What if the measurements were in centimeters instead of inches? A: The calculation remains the same; only the units change. The result would be 4 ⅛ square centimeters.
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes the result easier to understand and interpret. It also helps to avoid errors in further calculations.
-
Q: What other real-world applications exist for this measurement? A: The applications are vast. Think of tile layouts, the dimensions of picture frames, the sizing of fabric for clothing, or even the dimensions of a small garden plot.
Conclusion: Mastering Fractions for Real-World Success
Understanding the seemingly simple calculation of 1 ¼ x 3 ¼ unveils a broader appreciation for the power and practical applications of fractions in everyday life. From construction projects to culinary creations, the ability to confidently work with fractions ensures accuracy and efficiency. Mastering these fundamental mathematical concepts opens doors to countless opportunities and allows for precise execution in a multitude of fields. The seemingly simple 1 ¼ x 3 ¼ is a gateway to a deeper understanding of the mathematical principles that underpin our world. Remember the importance of accurate conversions, careful multiplication, and thorough simplification to ensure you achieve accurate and reliable results.
Latest Posts
Latest Posts
-
How Many Neutrons In Sodium
Sep 25, 2025
-
Orlando Florida Average Monthly Temperatures
Sep 25, 2025
-
Best Place To Take Temperature
Sep 25, 2025
-
Formula For A Rectangle Perimeter
Sep 25, 2025
-
Evil To Triumph Do Nothing
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 1 4 X 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.