1 Tan 2x Sec 2x
plugunplug
Sep 24, 2025 · 5 min read
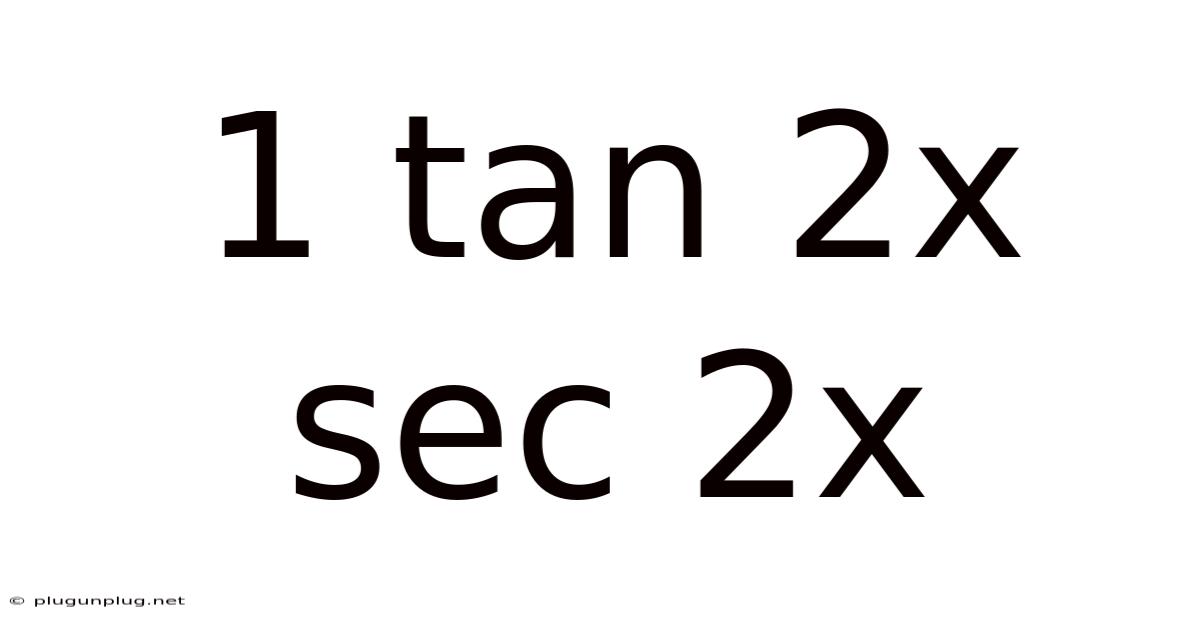
Table of Contents
Decoding the Trigonometric Expression: 1 + tan²x sec²x
This article delves into the trigonometric expression 1 + tan²x sec²x, exploring its simplification, derivation, and applications. We will unravel the seemingly complex expression, revealing its elegant underlying simplicity and demonstrating its practical use in various mathematical contexts. Understanding this expression is crucial for anyone studying trigonometry, calculus, or related fields. We'll break down the process step-by-step, making it accessible even to those with a basic understanding of trigonometry.
Introduction: Unpacking the Fundamentals
Before diving into the simplification of 1 + tan²x sec²x, let's refresh our understanding of the fundamental trigonometric identities. These identities form the bedrock of trigonometric manipulation and are essential for solving complex expressions. The key identities we'll be leveraging include:
- Pythagorean Identities: These identities stem directly from the Pythagorean theorem and relate the squares of sine, cosine, and tangent functions. The most relevant for our purpose is: 1 + tan²x = sec²x.
- Reciprocal Identities: These identities define the relationships between the primary trigonometric functions (sine, cosine, tangent) and their reciprocals (cosecant, secant, cotangent). Crucially for our problem, we have: sec x = 1/cos x and tan x = sin x / cos x.
These identities are not merely abstract formulas; they represent fundamental geometric relationships within a right-angled triangle. Understanding their geometric interpretation strengthens intuition and simplifies the process of manipulating trigonometric expressions.
Simplifying 1 + tan²x sec²x: A Step-by-Step Approach
Now, let's tackle the simplification of our target expression: 1 + tan²x sec²x. The process is straightforward if we apply the fundamental trigonometric identities strategically.
Step 1: Utilize the Pythagorean Identity
The most obvious starting point is to recognize the Pythagorean identity: 1 + tan²x = sec²x. While this doesn't directly address the entire expression, it offers a valuable substitution opportunity. We can rewrite the expression as:
sec²x sec²x
Step 2: Simplify the Expression
This simplifies our expression considerably:
sec⁴x
Therefore, 1 + tan²x sec²x simplifies to sec⁴x. This seemingly complex expression boils down to a concise and elegant result through the application of a fundamental trigonometric identity.
Alternative Approach: Expanding the Expression
While the method above is the most efficient, let's explore an alternative approach that demonstrates the power of expanding the expression using the reciprocal and quotient identities.
Step 1: Expand using Reciprocal and Quotient Identities
We begin by substituting the reciprocal and quotient identities into the original expression:
1 + (sin²x / cos²x) * (1 / cos²x)
Step 2: Simplify the Fraction
Combining the terms, we get:
1 + sin²x / cos⁴x
Step 3: Find a Common Denominator
To combine the terms, we need a common denominator:
(cos⁴x + sin²x) / cos⁴x
Step 4: Reaching the Simplified Form
At this stage, it might seem we've reached an impasse. However, this expression, while correct, isn't simplified. To achieve the simplified form, we can proceed with a bit more manipulation. This alternative route is generally less efficient but provides valuable insight into the relationships between different trigonometric functions. This route requires additional steps and a deeper understanding of trigonometric identities, particularly those related to sine and cosine. Although we can't directly simplify this expression further to reach sec⁴x with this method, it showcases the diverse approaches available and the interconnectedness of trigonometric concepts.
The Geometric Interpretation: Visualizing the Expression
Trigonometric functions aren't merely abstract algebraic entities; they represent geometric relationships within a right-angled triangle. Visualizing these relationships provides crucial insight into the meaning and behavior of trigonometric expressions. The expression 1 + tan²x sec²x can be understood geometrically by considering the right-angled triangle. The tangent and secant functions are defined in terms of the sides of the triangle. By examining the ratios between the sides and relating them to the Pythagorean theorem, the simplification of the expression becomes more intuitive. This geometric perspective helps to solidify the abstract algebraic manipulations and offers a powerful tool for conceptual understanding. However, a fully detailed geometric proof requires detailed diagrammatic representation which is beyond the scope of this text-based format.
Applications in Calculus and Other Fields
The simplification of 1 + tan²x sec²x, and more importantly, the understanding of the underlying trigonometric identities, finds broad application in various mathematical fields:
- Calculus: This simplification is frequently encountered during integration and differentiation of trigonometric functions. Simplifying expressions using identities is crucial for simplifying complex integrals and derivatives, making them more manageable and solvable.
- Differential Equations: Trigonometric identities play a crucial role in solving differential equations, particularly those that model oscillatory phenomena.
- Physics and Engineering: Trigonometry, and its identities, is fundamental to fields like physics and engineering, particularly in areas involving oscillations, waves, and rotations. Understanding the expression 1 + tan²x sec²x directly contributes to a deeper understanding of these physical processes.
Frequently Asked Questions (FAQ)
-
Q: Can this expression be simplified further than sec⁴x?
A: No, sec⁴x is the most simplified form of the expression 1 + tan²x sec²x using standard trigonometric identities.
-
Q: What are the limitations of this simplification?
A: The simplification is valid for all values of x where the functions tan x and sec x are defined (i.e., cos x ≠ 0). At points where cos x = 0, the expression is undefined.
-
Q: Are there other trigonometric identities that could be used to simplify this expression?
A: While the Pythagorean identity is the most direct and efficient approach, other identities can be incorporated, but they will likely lead to a longer and more convoluted simplification process.
Conclusion: Mastering Trigonometric Identities
Mastering trigonometric identities is crucial for success in mathematics, particularly in calculus and related fields. The simplification of 1 + tan²x sec²x, though seemingly challenging at first glance, becomes straightforward with a methodical approach and a solid understanding of the fundamental identities. The journey from the initial complex expression to its simplified form (sec⁴x) highlights the power and elegance of trigonometric manipulation. Remember, the key is to practice consistently and cultivate a deep understanding of the underlying geometric interpretations of these identities. This approach not only aids in solving specific problems but also fosters a broader mathematical intuition that proves invaluable in more advanced studies. By combining a thorough understanding of the theoretical underpinnings with consistent practice, you will gain the confidence to tackle even the most challenging trigonometric problems with ease.
Latest Posts
Latest Posts
-
Give Human Qualities To Animals
Sep 24, 2025
-
What Does A Stem Do
Sep 24, 2025
-
10to The Power Of 5
Sep 24, 2025
-
Mg To Ml Conversion Calculator
Sep 24, 2025
-
What Does Avpu Stand For
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 Tan 2x Sec 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.