11 25 As A Decimal
plugunplug
Sep 17, 2025 · 5 min read
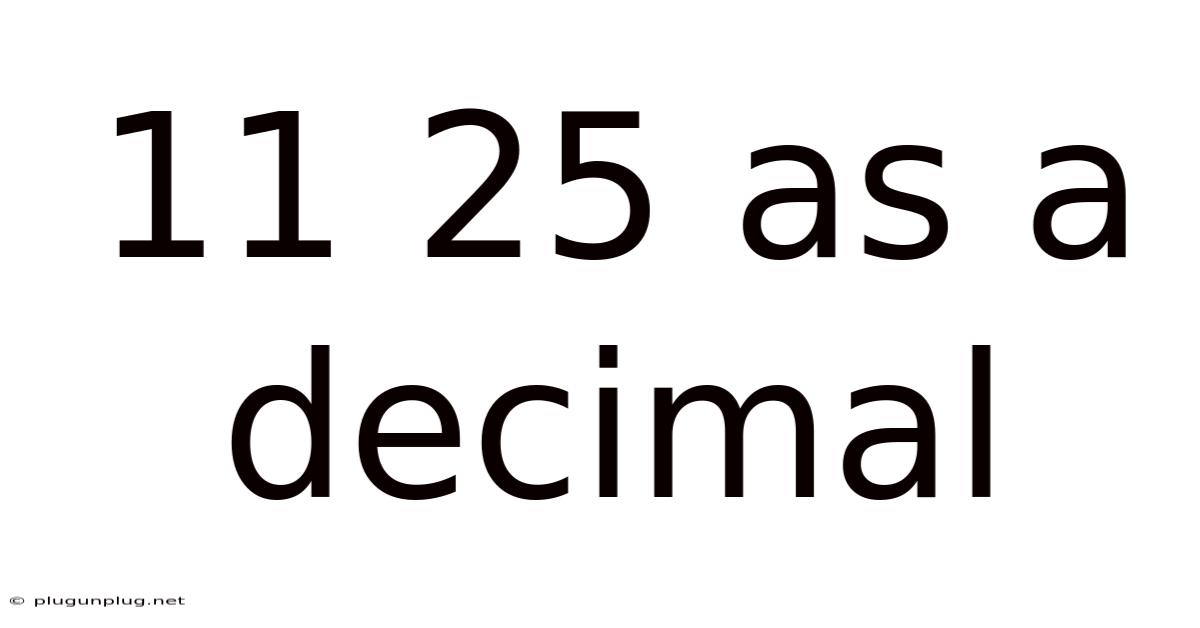
Table of Contents
11/25 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the conversion of the fraction 11/25 into its decimal equivalent, explaining the process in detail and exploring related concepts. We'll cover various methods, address common misconceptions, and answer frequently asked questions to provide a thorough understanding of this seemingly simple yet important mathematical concept.
Introduction: Understanding Fractions and Decimals
Before diving into the conversion of 11/25, let's briefly revisit the fundamentals of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000). Decimals use a decimal point to separate the whole number part from the fractional part.
The conversion between fractions and decimals is essentially a process of expressing the same value in a different format. This is particularly useful when performing calculations, as decimals are often easier to manipulate in many arithmetic operations.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. In this case, we divide the numerator (11) by the denominator (25):
11 ÷ 25 = 0.44
Therefore, 11/25 as a decimal is 0.44. This method is simple and readily applicable using a calculator or manual long division.
Method 2: Converting the Denominator to a Power of 10
This method involves manipulating the fraction to have a denominator that is a power of 10 (10, 100, 1000, etc.). This is achieved by finding an equivalent fraction. Since 25 is a factor of 100 (25 x 4 = 100), we can multiply both the numerator and the denominator by 4:
(11 x 4) / (25 x 4) = 44/100
Now, expressing 44/100 as a decimal is straightforward. The denominator, 100, indicates two decimal places. Therefore:
44/100 = 0.44
This method reinforces the understanding of equivalent fractions and provides an alternative approach to the direct division method.
Method 3: Using Decimal Equivalents of Common Fractions
Familiarizing yourself with the decimal equivalents of common fractions can speed up the conversion process. Knowing that 1/4 = 0.25, we can deduce that 11/25 is simply 11 times 1/25. Since 1/25 is 1/4 of 1/10 (1/100), this approach offers another perspective on fraction to decimal conversion.
1/25 = 0.04 (because 1/25 = 4/100 = 0.04). 11/25 = 11 * (1/25) = 11 * 0.04 = 0.44
Understanding the Decimal Representation: Significance and Applications
The decimal representation of 11/25, which is 0.44, signifies that it represents 44 hundredths or 44 out of 100 equal parts of a whole. This simple decimal holds various applications across numerous fields.
- Financial Calculations: Percentages are often expressed as decimals. For instance, a 44% discount would be represented as 0.44 in calculations.
- Scientific Measurements: Many scientific measurements involve decimals, whether in length, weight, or other physical quantities. The precision offered by decimals is essential for accurate representation.
- Data Analysis: In statistical analysis, data is often presented and manipulated using decimals, offering a clear and concise way to represent various findings and probabilities.
- Computer Programming: Computer programs heavily rely on numerical representations, often using decimals to represent fractional values.
- Everyday Life: From calculating tips in restaurants to measuring ingredients in recipes, a basic understanding of decimal representation is quite handy.
Further Exploration: Converting Other Fractions to Decimals
The methods described above are universally applicable to converting any fraction to its decimal equivalent. However, some fractions may result in recurring decimals (decimals that repeat infinitely), like 1/3 (0.3333...). These decimals may need to be rounded off for practical purposes. Understanding the concept of recurring decimals and the implications of rounding is crucial for accuracy in calculations involving these types of fractions.
Addressing Common Misconceptions
A common misconception is that all fractions can be converted to terminating decimals (decimals that end). This is not true; some fractions result in recurring decimals. Another misconception involves incorrectly multiplying only the numerator or the denominator when converting to an equivalent fraction with a power-of-10 denominator. Both the numerator and the denominator must be multiplied by the same number to maintain the value of the fraction.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest method to convert 11/25 to a decimal?
- A: The simplest method is direct division: 11 ÷ 25 = 0.44.
-
Q: Can 11/25 be expressed as a percentage?
- A: Yes, 0.44 is equivalent to 44%.
-
Q: What if the denominator of a fraction is not easily converted to a power of 10?
- A: In such cases, direct division is the most straightforward approach. Alternatively, you can use long division to find the decimal equivalent.
-
Q: How do I handle fractions that result in recurring decimals?
- A: Recurring decimals often need to be rounded off to a certain number of decimal places for practical applications. The level of precision required depends on the context of the problem.
-
Q: Is there a way to convert decimals back to fractions?
- A: Yes, decimals can be converted back to fractions by expressing the decimal as a fraction with a power of 10 as the denominator and then simplifying the fraction to its lowest terms. For example, 0.44 can be written as 44/100, which simplifies to 11/25.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental mathematical skill with far-reaching applications. Understanding the different methods available, such as direct division and converting the denominator to a power of 10, empowers you to approach these conversions with confidence and efficiency. While seemingly simple, mastering this skill strengthens your overall mathematical proficiency and lays a solid foundation for more complex calculations and concepts. By understanding the principles involved and addressing common misconceptions, you'll develop a strong grasp of this crucial aspect of mathematics. Remember to practice regularly to enhance your speed and accuracy in converting fractions to decimals and vice versa. This skill will undoubtedly prove valuable in various academic and real-world scenarios.
Latest Posts
Latest Posts
-
How Long Is 20 Miles
Sep 17, 2025
-
Diameter Of A Tennis Ball
Sep 17, 2025
-
Hcf Of 12 And 30
Sep 17, 2025
-
10 Facts About Hitlers Childhood
Sep 17, 2025
-
Rhyme To Learn The Planets
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 11 25 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.