18 20 As A Percent
plugunplug
Sep 23, 2025 · 5 min read
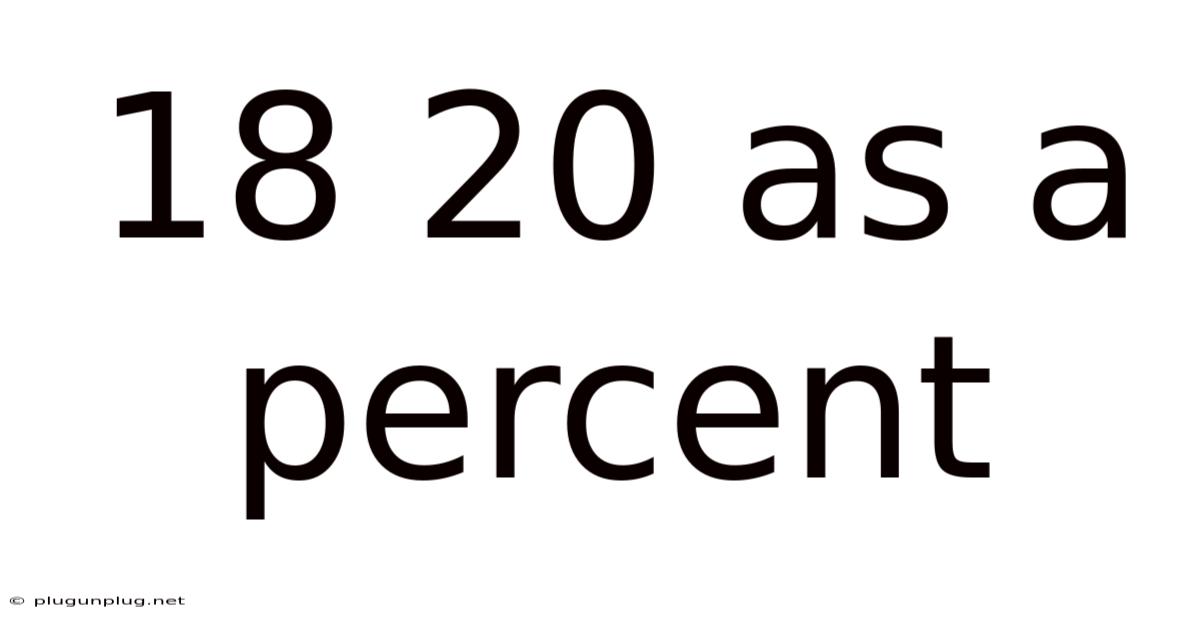
Table of Contents
18/20 as a Percent: Understanding Fractions, Decimals, and Percentages
Converting fractions to percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating grades and discounts to understanding statistics and financial reports. This article will thoroughly explain how to convert the fraction 18/20 into a percentage, detailing the process step-by-step and exploring the underlying mathematical principles. We'll also delve into related concepts and answer frequently asked questions to ensure a comprehensive understanding.
Introduction: The Importance of Percentage Conversions
Percentages are a way of expressing a number as a fraction of 100. They provide a standardized method for comparing proportions and making numerical relationships easier to understand. Understanding how to convert fractions and decimals to percentages is crucial for various fields, including:
- Academics: Calculating grades, test scores, and assignment marks.
- Finance: Understanding interest rates, discounts, and profit margins.
- Statistics: Interpreting data and presenting findings in a clear and concise manner.
- Everyday Life: Calculating tips, sales tax, and comparing prices.
The fraction 18/20, often encountered in academic settings or everyday calculations, represents a part-to-whole relationship. Converting it to a percentage allows for easier comparison with other ratios expressed as percentages. This article will guide you through the process, ensuring you not only understand the calculation for 18/20 but also grasp the broader concepts involved.
Method 1: Converting the Fraction Directly
The most straightforward approach to converting 18/20 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: To do this, divide the numerator (18) by the denominator (20). 18 ÷ 20 = 0.9
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.9 x 100 = 90%
Therefore, 18/20 is equal to 90%.
Method 2: Simplifying the Fraction First
Before converting to a decimal and then a percentage, you can simplify the fraction 18/20. This step isn't strictly necessary but can make the calculation easier. Both 18 and 20 are divisible by 2:
18 ÷ 2 = 9 20 ÷ 2 = 10
This simplifies the fraction to 9/10. Now, repeat the steps from Method 1:
-
Convert the simplified fraction to a decimal: 9 ÷ 10 = 0.9
-
Convert the decimal to a percentage: 0.9 x 100 = 90%
Again, we arrive at the answer: 18/20 = 90%. Simplifying the fraction beforehand can be helpful, especially when dealing with larger numbers.
Method 3: Using Proportions
Another approach involves setting up a proportion. We know that a percentage is a fraction out of 100. We can set up the following proportion:
18/20 = x/100
To solve for 'x' (the percentage), cross-multiply:
18 * 100 = 20 * x 1800 = 20x
Now, divide both sides by 20:
x = 1800 / 20 x = 90
Therefore, x = 90%, confirming our previous results.
Understanding the Mathematical Principles
The conversion from a fraction to a percentage fundamentally relies on the concept of proportionality. A percentage represents a proportion out of 100. When we divide the numerator by the denominator, we're finding the decimal equivalent, representing the fraction's value as a part of one whole. Multiplying by 100 then scales this decimal to express it as a part of 100, giving us the percentage.
The simplification of fractions is based on the concept of equivalent fractions. Dividing both the numerator and denominator by their greatest common divisor (GCD) maintains the value of the fraction while reducing its complexity. In the case of 18/20, the GCD is 2. Simplifying makes calculations easier and can lead to a clearer understanding of the underlying relationship.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages is invaluable in various real-world scenarios. Consider these examples:
- Academic Performance: If a student answers 18 out of 20 questions correctly on a test, their score is 90%. This provides a clear and easily understandable representation of their performance.
- Sales and Discounts: A store offering a 10% discount on an item priced at $20 would reduce the price by $2 (10% of $20). Understanding this requires converting the percentage back into a decimal or fraction.
- Financial Investments: Calculating the return on investment (ROI) involves converting the profit made into a percentage of the initial investment.
- Data Analysis: In statistical analysis, data is often represented as percentages to facilitate comparisons and interpretations.
Frequently Asked Questions (FAQ)
-
Q: What if the fraction doesn't simplify easily?
A: Even if the fraction doesn't simplify neatly, you can still use the direct method (Method 1) of dividing the numerator by the denominator and then multiplying by 100. Calculators are very helpful in these situations.
-
Q: Can I convert percentages back to fractions?
A: Absolutely! To convert a percentage to a fraction, simply divide the percentage by 100 and simplify the resulting fraction. For example, 90% becomes 90/100, which simplifies to 9/10.
-
Q: What if I have a decimal that extends beyond several places?
A: Rounding the decimal to a suitable number of decimal places is generally acceptable depending on the required level of accuracy. For most everyday applications, rounding to two decimal places is usually sufficient.
-
Q: How can I improve my understanding of fractions and percentages?
A: Practice is key! Work through various examples, try different methods, and familiarize yourself with the underlying mathematical principles. Online resources and educational materials can offer additional support.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with far-reaching applications. This article detailed three methods for converting 18/20 to its percentage equivalent (90%), emphasizing the underlying mathematical principles. By understanding these principles and practicing the conversion methods, you will develop confidence and proficiency in handling various mathematical problems involving fractions, decimals, and percentages in academic settings and daily life. Remember that the ability to smoothly transition between these representations enhances your mathematical literacy and problem-solving abilities.
Latest Posts
Latest Posts
-
Theme Of The Poem London
Sep 23, 2025
-
G Ml To Kg M3
Sep 23, 2025
-
Function Of The Waxy Cuticle
Sep 23, 2025
-
Fall Onto An Outstretched Hand
Sep 23, 2025
-
How Can You Challenge Discrimination
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 18 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.