19 20 As A Percentage
plugunplug
Sep 17, 2025 · 6 min read
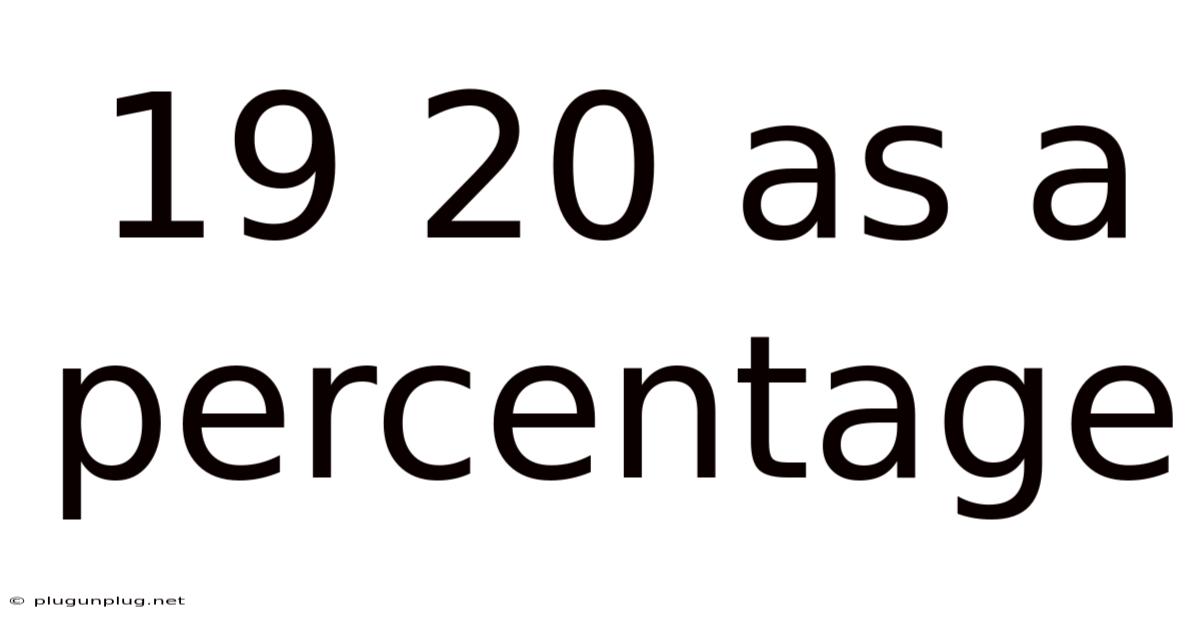
Table of Contents
Decoding 19/20 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves into the specific calculation of representing 19 out of 20 as a percentage, providing a detailed explanation, different methods for solving it, and exploring the broader context of percentage calculations. This will equip you with the knowledge and confidence to tackle similar problems and strengthen your grasp of this essential mathematical concept.
Understanding Percentages: The Basics
Before we dive into calculating 19/20 as a percentage, let's refresh our understanding of what a percentage actually represents. A percentage is simply a fraction where the denominator is always 100. It represents a portion or proportion of a whole, expressed as a number out of 100. The symbol "%" is used to denote a percentage.
For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental relationship between fractions, decimals, and percentages is crucial for solving percentage problems.
Method 1: The Direct Conversion Method
The most straightforward way to convert a fraction to a percentage is to first express the fraction as a decimal and then multiply by 100. Let's apply this method to calculate 19/20 as a percentage:
-
Convert the fraction to a decimal: To do this, we divide the numerator (19) by the denominator (20):
19 ÷ 20 = 0.95
-
Multiply the decimal by 100: This converts the decimal to a percentage:
0.95 x 100 = 95%
Therefore, 19/20 is equal to 95%.
Method 2: The Proportion Method
This method uses the concept of proportions to solve for the percentage. We set up a proportion where one ratio represents the given fraction (19/20) and the other represents the unknown percentage (x/100):
19/20 = x/100
To solve for x (the percentage), we cross-multiply:
19 * 100 = 20 * x
1900 = 20x
Now, divide both sides by 20:
x = 1900 ÷ 20
x = 95
Therefore, 19/20 is equivalent to 95%. This method reinforces the understanding of the relationship between fractions and percentages.
Method 3: Using Percentage as a Multiplier
This approach utilizes the fact that a percentage can be expressed as a decimal multiplier. To find a percentage of a number, we multiply the number by the decimal equivalent of the percentage. In this case, we can consider 19 as the percentage of 20. We want to find what percentage of 20 is 19. We set up the equation:
19 = x * 20
To solve for x (the percentage in decimal form), we divide both sides by 20:
x = 19 ÷ 20
x = 0.95
Now, convert this decimal to a percentage by multiplying by 100:
0.95 * 100 = 95%
Thus, 19 is 95% of 20.
Interpreting the Result: What Does 95% Mean?
Achieving a score of 19 out of 20 represents a remarkably high level of performance. The 95% score indicates that the individual or entity in question has successfully completed or answered 95 out of every 100 possible items correctly. This level of accuracy suggests a strong understanding of the subject matter and proficiency in the task at hand. In many academic or professional contexts, a score of this magnitude often signifies excellence.
Real-World Applications of Percentage Calculations
The ability to convert fractions to percentages is indispensable in numerous real-life scenarios. Here are just a few examples:
-
Academic Grades: Converting test scores or assignment marks into percentages provides a standardized way to evaluate performance and compare results across different assessments.
-
Financial Calculations: Percentages are crucial in understanding interest rates, discounts, taxes, and investment returns. Calculating percentage increases or decreases helps in tracking financial progress.
-
Data Analysis: In statistics and data analysis, percentages are used to represent proportions of data, making it easier to visualize and interpret trends and patterns.
-
Sales and Marketing: Businesses use percentages to calculate discounts, markups, profit margins, and sales growth.
-
Everyday Life: We encounter percentage calculations in everyday life, such as calculating tips in restaurants, understanding sale prices in stores, and interpreting nutritional information on food labels.
Frequently Asked Questions (FAQ)
Q1: How do I convert other fractions to percentages?
A: You can use any of the methods described above to convert any fraction to a percentage. The core principle remains the same: divide the numerator by the denominator and multiply the result by 100.
Q2: What if the fraction is an improper fraction (numerator is larger than denominator)?
A: You can still use the same methods. The resulting percentage will be greater than 100%. For example, 21/20 converted to a percentage is (21 ÷ 20) * 100 = 105%.
Q3: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have a percentage function that simplifies the conversion process. Simply divide the numerator by the denominator and then press the percentage key.
Q4: What is the difference between a percentage and a decimal?
A: A percentage is a fraction with a denominator of 100, while a decimal is a fraction expressed in tenths, hundredths, thousandths, and so on. They are essentially different ways of representing the same value. A percentage can be easily converted to a decimal by dividing it by 100.
Beyond the Basics: Advanced Percentage Calculations
While this article focuses on the conversion of 19/20 to a percentage, understanding percentages opens the door to more complex calculations, including:
-
Percentage change: Calculating the percentage increase or decrease between two values.
-
Percentage of a percentage: Finding a percentage of a given percentage.
-
Compound percentage: Calculating the effect of repeated percentage changes.
-
Percentage points: Understanding the difference between percentage change and percentage points.
Mastering percentage calculations will undoubtedly enhance your mathematical proficiency and make you more adept at tackling various challenges in academic, professional, and personal life. The ability to confidently work with percentages is a valuable skill that will serve you well in many contexts.
Conclusion
Calculating 19/20 as a percentage yields a result of 95%, representing a high level of achievement or accuracy. This article explored various methods to reach this solution, emphasizing the fundamental concepts underlying percentage calculations. By understanding these methods and their applications, you can confidently tackle similar problems and apply this knowledge to a vast array of real-world situations, improving your mathematical competence and overall problem-solving abilities. Remember that practice is key to mastering any mathematical concept, so don't hesitate to apply these techniques to other fractions and problems to solidify your understanding.
Latest Posts
Latest Posts
-
What Is 20 Of 45 00
Sep 17, 2025
-
Convert Pounds To Kilograms Formula
Sep 17, 2025
-
How Many Living Wwii Veterans
Sep 17, 2025
-
Diagram Of A Lipid Bilayer
Sep 17, 2025
-
30 Days Past September Poem
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 19 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.