2 1/7 + 1 1/4
plugunplug
Sep 17, 2025 · 5 min read
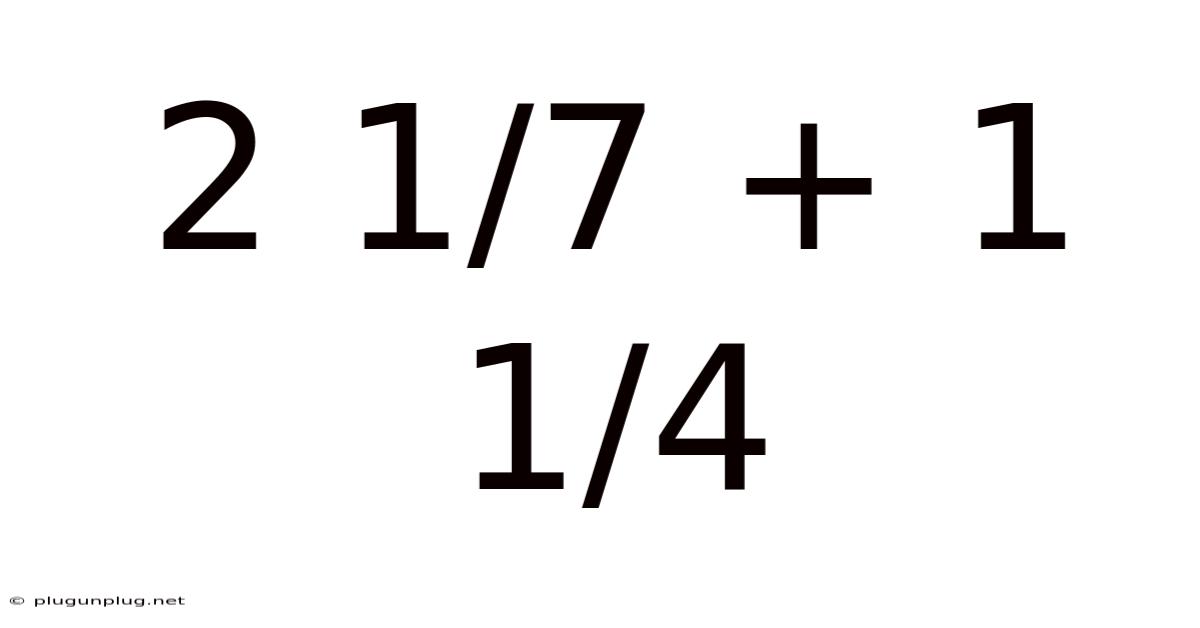
Table of Contents
Decoding Fractions: A Deep Dive into 2 1/7 + 1 1/4
Adding fractions might seem like a simple arithmetic task, but mastering it opens doors to a deeper understanding of mathematical concepts crucial for higher-level studies. This article will guide you through the process of solving 2 1/7 + 1 1/4, not just providing the answer, but explaining the underlying principles and offering valuable insights into working with mixed numbers and fractions in general. We'll break down the problem step-by-step, exploring different methods, and address common misconceptions. By the end, you'll be confident in tackling similar fraction problems and have a solid foundation in fraction arithmetic.
Understanding Mixed Numbers and Improper Fractions
Before we dive into the addition, let's clarify some fundamental terms. A mixed number combines a whole number and a fraction, like 2 1/7 and 1 1/4. An improper fraction, on the other hand, has a numerator (top number) larger than or equal to its denominator (bottom number). To add mixed numbers effectively, we often convert them into improper fractions.
Let's convert our mixed numbers:
-
2 1/7: To convert this to an improper fraction, we multiply the whole number (2) by the denominator (7), add the numerator (1), and keep the same denominator. This gives us (2 * 7) + 1 / 7 = 15/7
-
1 1/4: Similarly, for this mixed number, we calculate (1 * 4) + 1 / 4 = 5/4
Finding a Common Denominator: The Key to Fraction Addition
The core principle of adding fractions is to have a common denominator. This means both fractions need to have the same denominator before we can add their numerators. Think of it like adding apples and oranges – you can't directly add them unless you express them in a common unit.
In our case, we need to find a common denominator for 7 and 4. The easiest way is to find the least common multiple (LCM) of 7 and 4. Since 7 is a prime number and 4 = 2 x 2, the LCM is simply 7 x 4 = 28.
Now, let's convert our improper fractions to have a denominator of 28:
-
15/7: To get a denominator of 28, we multiply both the numerator and the denominator by 4: (15 x 4) / (7 x 4) = 60/28
-
5/4: To get a denominator of 28, we multiply both the numerator and the denominator by 7: (5 x 7) / (4 x 7) = 35/28
Adding the Fractions
With both fractions having the same denominator (28), we can now add them by simply adding their numerators:
60/28 + 35/28 = (60 + 35) / 28 = 95/28
Converting Back to a Mixed Number
The result, 95/28, is an improper fraction. To make it easier to understand, let's convert it back to a mixed number. We do this by dividing the numerator (95) by the denominator (28):
95 ÷ 28 = 3 with a remainder of 11
This means that 95/28 is equivalent to 3 11/28. Therefore, the solution to 2 1/7 + 1 1/4 is 3 11/28.
Alternative Methods: The "Borrowing" Technique
While the method above is straightforward, there's an alternative approach involving working directly with the mixed numbers. This involves "borrowing" from the whole numbers if necessary. Let’s explore this:
-
Find the Common Denominator: As before, the least common denominator for 7 and 4 is 28.
-
Rewrite the Mixed Numbers: Rewrite the mixed numbers with the common denominator:
- 2 1/7 becomes 2 4/28 (we multiplied the numerator and denominator of 1/7 by 4)
- 1 1/4 becomes 1 7/28 (we multiplied the numerator and denominator of 1/4 by 7)
-
Add the Whole Numbers and Fractions Separately: Add the whole numbers: 2 + 1 = 3. Add the fractions: 4/28 + 7/28 = 11/28
-
Combine the Results: Combine the sum of the whole numbers and the sum of the fractions to get the final answer: 3 11/28
Visualizing Fraction Addition: A Geometric Approach
Understanding fractions can be significantly enhanced through visualization. Imagine representing 2 1/7 as two whole circles and a seventh of a circle. Similarly, represent 1 1/4 as one whole circle and a quarter of a circle. Adding them visually would involve combining the whole circles and then finding a way to combine the fractional parts, necessitating finding a common denominator to represent the fractions using the same-sized pieces. This visual approach can make the concept more intuitive.
Frequently Asked Questions (FAQ)
Q1: Why is finding a common denominator so important?
A1: You can't directly add or subtract fractions with different denominators because they represent different-sized portions of a whole. Finding a common denominator ensures you are adding or subtracting like quantities.
Q2: Is there a quicker way to find the least common multiple (LCM)?
A2: For smaller numbers, listing multiples is often sufficient. For larger numbers, prime factorization can be a more efficient method. Prime factorization breaks down numbers into their prime factors, and the LCM is found by taking the highest power of each prime factor present in the numbers.
Q3: What if I get an improper fraction as the answer?
A3: It's perfectly acceptable to leave your answer as an improper fraction, but converting it to a mixed number is generally preferred for easier interpretation.
Q4: Can I use a calculator to solve fraction problems?
A4: While calculators can be helpful for verifying answers, it's crucial to understand the underlying mathematical concepts. Using a calculator without understanding the process hinders your learning.
Q5: Are there any other types of fraction problems?
A5: Yes, besides addition, you'll also encounter subtraction, multiplication, and division of fractions, each with its own set of rules and techniques.
Conclusion: Mastering Fraction Arithmetic
Adding fractions, even with mixed numbers, becomes manageable with a systematic approach. Understanding the concept of a common denominator is crucial. While calculators can assist, mastering the manual process is essential for building a robust understanding of fractions and their applications in various fields, from basic arithmetic to advanced calculus and beyond. Remember to practice regularly to build your confidence and fluency. The more you work with fractions, the more intuitive the process will become, paving the way for success in more complex mathematical challenges.
Latest Posts
Latest Posts
-
Def Of The American Dream
Sep 17, 2025
-
What Are Mars Moons Called
Sep 17, 2025
-
First Feature Length Animated Movie
Sep 17, 2025
-
Half A Pound In Ounces
Sep 17, 2025
-
A Quadrilateral Is A Trapezoid
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2 1/7 + 1 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.