2 2 3 X 3
plugunplug
Sep 22, 2025 · 5 min read
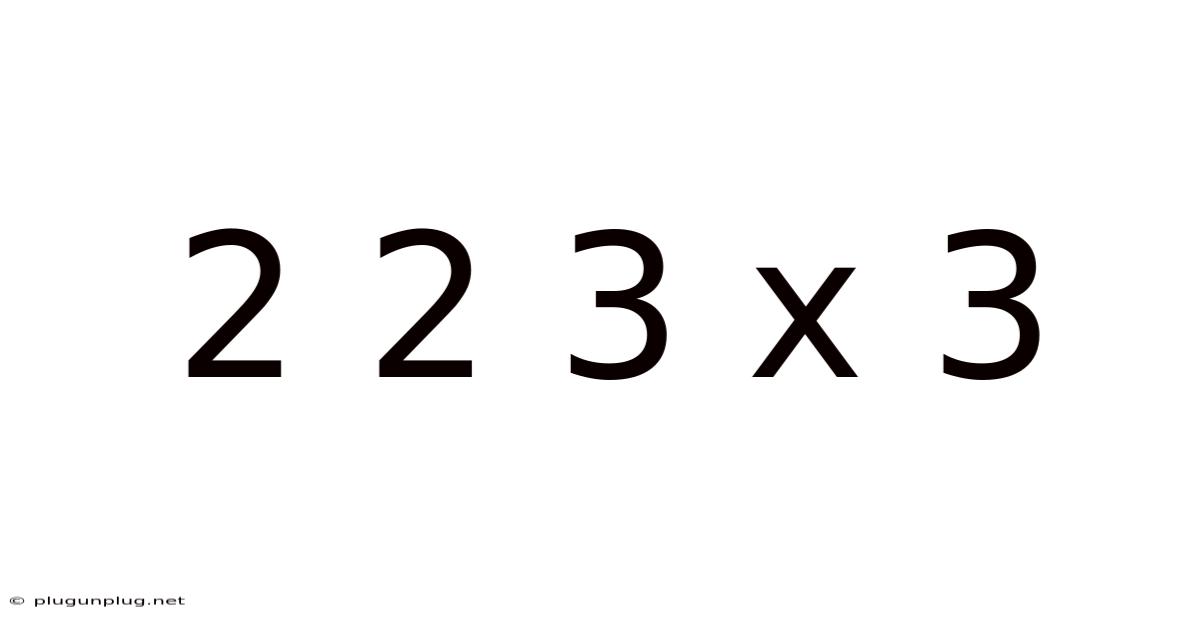
Table of Contents
Decoding 2 2 3 x 3: Exploring the Depths of Multiplication and Beyond
This article delves into the seemingly simple mathematical expression "2 2 3 x 3," unraveling its multiple interpretations, exploring the underlying principles of multiplication, and expanding on its implications within broader mathematical contexts. We'll move beyond the basic calculation to examine its significance in algebra, geometry, and even the philosophy of mathematics. This exploration aims to be comprehensive and accessible, suitable for readers of various mathematical backgrounds, from beginners to those seeking a deeper understanding.
Understanding the Basics: Order of Operations (PEMDAS/BODMAS)
Before we dissect "2 2 3 x 3," it's crucial to establish a foundational understanding of the order of operations. This dictates the sequence in which we perform calculations to arrive at a single, unambiguous answer. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) is commonly used. Both mnemonics represent the same order.
In our expression, "2 2 3 x 3," the absence of parentheses or exponents simplifies the process. We prioritize multiplication before addition. However, the ambiguous arrangement introduces the possibility of multiple interpretations.
Interpretation 1: (2 + 2 + 3) x 3
One interpretation treats the initial numbers as a sum before multiplication:
- Addition: 2 + 2 + 3 = 7
- Multiplication: 7 x 3 = 21
Therefore, under this interpretation, the answer is 21. This approach assumes a grouping of the initial numbers.
Interpretation 2: 2 + 2 + (3 x 3)
Another interpretation prioritizes the multiplication first:
- Multiplication: 3 x 3 = 9
- Addition: 2 + 2 + 9 = 13
In this case, the answer is 13. This interpretation clearly distinguishes the multiplication operation.
Interpretation 3: (2)(2)(3) x 3 (Implicit Multiplication)
Mathematically, the juxtaposition of numbers implies multiplication. We can interpret "2 2 3" as (2)(2)(3):
- Multiplication: (2)(2)(3) = 12
- Multiplication: 12 x 3 = 36
This approach yields an answer of 36. It leverages the implied multiplication inherent in the concise notation.
The Importance of Notation: Clarity in Mathematics
The ambiguity highlights the critical role of precise mathematical notation. Without parentheses or other clarifying symbols, the expression is open to multiple interpretations. In formal mathematics, we strive for unambiguous expressions to avoid confusion and ensure consistent results. Proper use of parentheses, brackets, and other symbols is fundamental to avoiding such ambiguity.
Expanding the Concept: Multiplication in Different Contexts
Let's move beyond the specific expression and explore the broader concept of multiplication.
-
Repeated Addition: Multiplication is fundamentally repeated addition. For example, 3 x 4 can be visualized as 4 + 4 + 4, or three groups of four. This visualization is particularly helpful for understanding multiplication's basic principles.
-
Cartesian Product: In set theory, multiplication represents the Cartesian product of sets. If set A has m elements and set B has n elements, the Cartesian product A x B has m x n elements. This concept extends multiplication's applications into more abstract areas of mathematics.
-
Scaling and Proportion: Multiplication is central to scaling and proportion. If we enlarge an image by a factor of 3, every dimension is multiplied by 3. This concept has vast applications in geometry, computer graphics, and engineering.
-
Algebraic Expressions: Multiplication is a fundamental operation in algebraic expressions. It's used to simplify, expand, and solve equations. Understanding multiplication's properties (commutative, associative, distributive) is essential for mastering algebra.
Geometric Interpretations: Area and Volume
Multiplication finds rich geometric interpretations.
-
Area of a Rectangle: The area of a rectangle is calculated by multiplying its length and width. This concept directly links multiplication to a tangible geometric property. The expression "3 x 4" can represent the area of a rectangle with sides of length 3 and 4 units.
-
Volume of a Rectangular Prism: Similarly, the volume of a rectangular prism (a three-dimensional box) is calculated by multiplying its length, width, and height. This extends the connection between multiplication and spatial dimensions.
Beyond the Numbers: The Philosophy of Mathematics
The seemingly simple act of calculating "2 2 3 x 3" touches upon deeper philosophical questions about the nature of mathematics itself:
-
Axiomatic Systems: Mathematical operations like multiplication are defined within axiomatic systems – sets of axioms (fundamental assumptions) and rules of inference. These systems provide a rigorous foundation for mathematical reasoning.
-
Consistency and Completeness: Mathematical systems aim to be both consistent (free from contradictions) and complete (capable of proving all true statements). The pursuit of consistency and completeness has been a central theme in the philosophy of mathematics for centuries.
-
The Nature of Numbers: The question of what numbers are has been debated by philosophers and mathematicians for millennia. Are they abstract entities existing independently of human thought, or are they human constructs? This question underlies the philosophical interpretation of mathematical operations.
Frequently Asked Questions (FAQ)
Q: What is the correct answer to "2 2 3 x 3"?
A: There's no single "correct" answer without clarifying the intended grouping. The possible answers, depending on interpretation, are 21, 13, and 36. The ambiguity highlights the need for clear notation.
Q: Why is it important to use parentheses in mathematical expressions?
A: Parentheses dictate the order of operations, ensuring unambiguous interpretation and consistent results. They are crucial for clarity and avoid potential errors.
Q: How does multiplication relate to other mathematical operations?
A: Multiplication is closely related to addition (repeated addition), division (its inverse operation), and exponentiation (repeated multiplication). Understanding these relationships is key to mastering arithmetic and algebra.
Q: What are some real-world applications of multiplication?
A: Multiplication has countless applications in everyday life, including calculating costs, measuring areas and volumes, scaling recipes, and numerous engineering and scientific calculations.
Conclusion: Beyond the Calculation
The seemingly simple expression "2 2 3 x 3" opens a door to a vast world of mathematical concepts. It underscores the importance of precise notation, highlights the interconnectedness of various mathematical operations, and even touches upon the philosophical underpinnings of mathematics itself. By exploring its various interpretations and extending the discussion to broader mathematical contexts, we hope this article has not only provided an answer but has also deepened your appreciation for the elegance and complexity inherent in even the simplest mathematical expressions. The journey of understanding mathematics is continuous, and every calculation, no matter how simple it may appear, offers opportunities for exploration and growth.
Latest Posts
Latest Posts
-
What Is An Optimum Temperature
Sep 22, 2025
-
3 Meters How Many Centimeters
Sep 22, 2025
-
Convert Mpg To Km Liter
Sep 22, 2025
-
33 60 As A Percentage
Sep 22, 2025
-
11 20 As A Percent
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 2 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.