24 9 In Simplest Form
plugunplug
Sep 17, 2025 · 5 min read
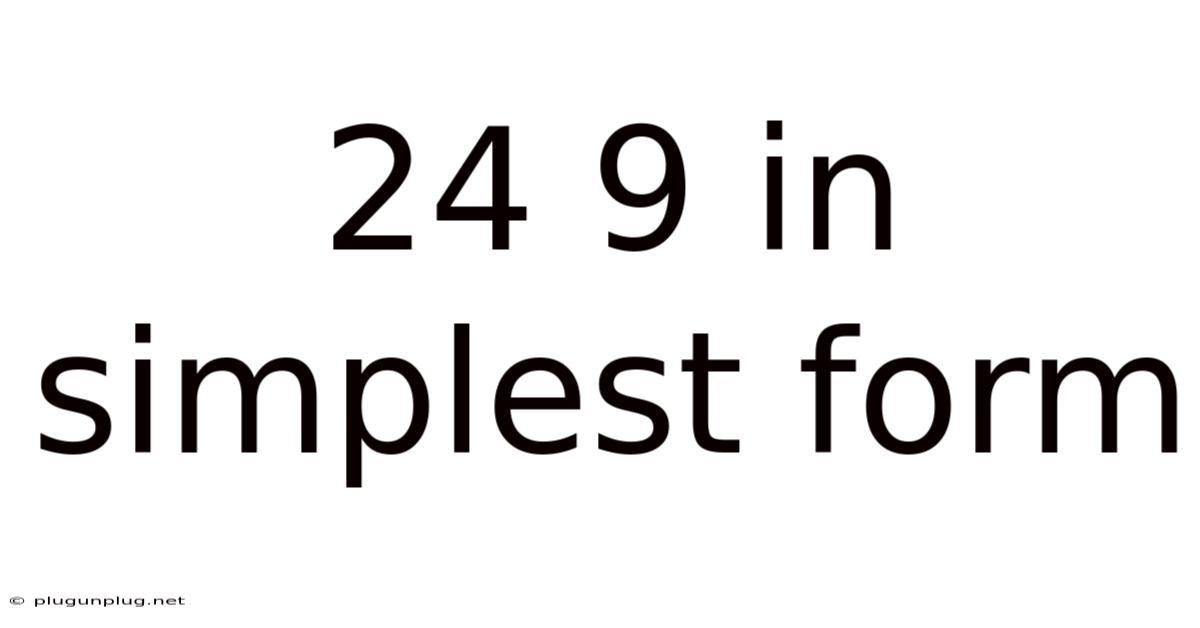
Table of Contents
Simplifying 24/9: A Comprehensive Guide to Fraction Reduction
Understanding how to simplify fractions is a fundamental skill in mathematics. This guide will delve into the process of simplifying the fraction 24/9, explaining the steps involved, the underlying mathematical principles, and addressing common questions. We'll move beyond just finding the answer and explore the broader concepts of greatest common divisors (GCD) and equivalent fractions, ensuring you develop a thorough grasp of the topic.
Introduction: What Does "Simplifying a Fraction" Mean?
Simplifying a fraction, also known as reducing a fraction to its simplest form or expressing it in lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. In essence, we're looking for the smallest whole numbers that represent the same ratio. The fraction 24/9 represents the ratio of 24 to 9, and simplifying it means finding a smaller, equivalent ratio.
Step-by-Step Simplification of 24/9
The most straightforward method for simplifying a fraction involves finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder.
-
Find the Factors of the Numerator (24): The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
-
Find the Factors of the Denominator (9): The factors of 9 are 1, 3, and 9.
-
Identify the Greatest Common Factor: Comparing the lists, we see that the largest number that appears in both lists is 3. Therefore, the greatest common divisor (GCD) of 24 and 9 is 3.
-
Divide Both the Numerator and Denominator by the GCD: We divide both the numerator (24) and the denominator (9) by the GCD (3):
24 ÷ 3 = 8 9 ÷ 3 = 3
-
The Simplified Fraction: This gives us the simplified fraction 8/3. This fraction is in its simplest form because 8 and 3 share no common factors other than 1.
Therefore, 24/9 simplified to its lowest terms is 8/3.
Understanding Equivalent Fractions
The process of simplifying fractions relies on the concept of equivalent fractions. Equivalent fractions represent the same value but have different numerators and denominators. For example, 24/9, 16/6, 8/3, and many others are all equivalent fractions. They all represent the same proportion or ratio. When we simplify a fraction, we are merely finding the most concise representation of that equivalent fraction set.
Methods for Finding the Greatest Common Divisor (GCD)
While listing factors is useful for smaller numbers like 24 and 9, it becomes less practical for larger numbers. Here are two more efficient methods for finding the GCD:
-
Prime Factorization: This method involves breaking down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- Prime factorization of 24: 2³ x 3
- Prime factorization of 9: 3²
- The common prime factor is 3. The lowest power of 3 is 3¹. Therefore, the GCD is 3.
-
Euclidean Algorithm: This algorithm is particularly efficient for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 24 by 9: 24 = 2 x 9 + 6
- Divide 9 by the remainder 6: 9 = 1 x 6 + 3
- Divide 6 by the remainder 3: 6 = 2 x 3 + 0
- The last non-zero remainder is 3, so the GCD is 3.
Improper Fractions and Mixed Numbers
The simplified fraction 8/3 is an improper fraction because the numerator (8) is larger than the denominator (3). Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction.
To convert 8/3 to a mixed number:
- Divide the numerator (8) by the denominator (3): 8 ÷ 3 = 2 with a remainder of 2.
- The whole number part of the mixed number is the quotient (2).
- The fractional part of the mixed number is the remainder (2) over the denominator (3).
Therefore, 8/3 is equivalent to the mixed number 2 2/3.
Applications of Fraction Simplification
Simplifying fractions is crucial in various mathematical contexts:
- Problem Solving: Simplifying fractions makes calculations easier and allows for a clearer understanding of the results.
- Comparisons: It's easier to compare fractions when they are in their simplest form.
- Algebra: Simplifying fractions is fundamental in algebraic manipulations and solving equations.
- Geometry: Fractions often appear in geometric calculations involving ratios and proportions.
Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes calculations simpler, easier to understand, and allows for easier comparisons. It's a fundamental skill in mathematics.
-
Q: What if I divide by a number that isn't the GCD?
- A: You'll still get an equivalent fraction, but it won't be in its simplest form. You'll need to repeat the simplification process until you find the GCD.
-
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
- A: No, you must divide both the numerator and the denominator by the same number to maintain the equivalent ratio.
-
Q: What if the GCD is 1?
- A: If the GCD is 1, the fraction is already in its simplest form.
-
Q: Are there any online tools to simplify fractions?
- A: While there are many online tools and calculators for simplifying fractions, understanding the underlying process is vital for mathematical proficiency.
Conclusion: Mastering Fraction Simplification
Simplifying fractions, such as reducing 24/9 to 8/3, is a cornerstone of mathematical understanding. By mastering this skill, you'll not only be able to solve problems more efficiently but also gain a deeper understanding of equivalent fractions, the greatest common divisor, and the interconnectedness of mathematical concepts. Remember the steps: find the GCD, divide both the numerator and denominator by the GCD, and express the result as an improper fraction or a mixed number if appropriate. With practice, this process will become second nature, allowing you to confidently tackle more complex mathematical challenges. The ability to simplify fractions is a valuable asset in various mathematical applications and helps build a strong foundation for future learning.
Latest Posts
Latest Posts
-
Which Organ Filters The Blood
Sep 17, 2025
-
Cuba Bay Of Pigs Summary
Sep 17, 2025
-
How Is A Stack Formed
Sep 17, 2025
-
Is 19 A Prime Number
Sep 17, 2025
-
Can Worcestershire Sauce Go Bad
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 24 9 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.