2x X 2x X 2x
plugunplug
Sep 18, 2025 · 6 min read
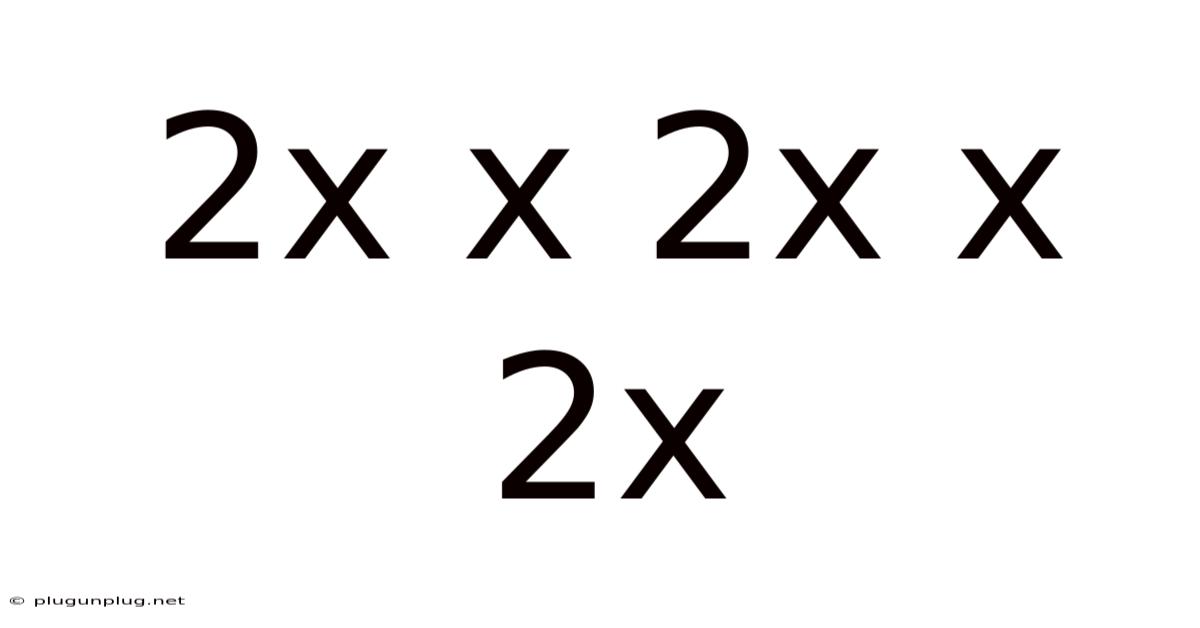
Table of Contents
Decoding 2x x 2x x 2x: Exploring Exponential Growth and its Real-World Applications
This article delves into the mathematical concept represented by "2x x 2x x 2x," focusing on its implications within exponential growth, its diverse applications across various fields, and its significance in understanding phenomena ranging from population dynamics to technological advancements. We'll unravel the underlying principles, explore practical examples, and address frequently asked questions, ensuring a comprehensive understanding of this seemingly simple yet powerful mathematical expression.
Understanding Exponential Growth: The Power of Repeated Multiplication
The expression "2x x 2x x 2x" fundamentally represents repeated multiplication, a core concept within exponential growth. Unlike linear growth, where a constant value is added repeatedly, exponential growth involves multiplying a base number (in this case, 2x) by itself repeatedly. The number of times the base is multiplied determines the exponent. In our example, we have a base of 2x and it's multiplied three times, so we can rewrite it as (2x)³.
This seemingly simple difference leads to dramatically different outcomes. While linear growth increases at a steady pace, exponential growth accelerates rapidly. This acceleration is particularly significant when the base number is greater than 1, as it is in our case. The larger the base and the higher the exponent, the faster the growth becomes. Imagine a single cell dividing into two, then those two dividing into four, and so on. This is a perfect illustration of exponential growth in nature.
Breaking Down the Expression: (2x)³
Let's dissect the expression (2x)³ further. According to the rules of exponents, this is equivalent to 2³ x x³. This simplifies to 8x³. Therefore, the expression "2x x 2x x 2x" ultimately represents eight times the cube of x. This seemingly simple transformation unlocks a deeper understanding of the underlying mathematical structure.
Real-World Applications: Where Exponential Growth Matters
The concept of exponential growth, represented by expressions like (2x)³, is ubiquitous across various fields. Let's examine some key applications:
1. Population Growth: Understanding population growth, whether it's of bacteria, animals, or humans, hinges on the principle of exponential growth. Under ideal conditions, populations tend to increase exponentially. This is because each individual can produce offspring, leading to a multiplicative increase in population size over time. Models utilizing exponential functions are essential for predicting future population sizes and managing resources accordingly.
2. Compound Interest: In finance, compound interest is a classic example of exponential growth. The interest earned in each period is added to the principal amount, and the next period's interest is calculated on this larger sum. This compounding effect leads to exponential growth of the investment over time. Understanding exponential growth is vital for making informed financial decisions, planning for retirement, and managing investments effectively.
3. Technological Advancements: Moore's Law, a widely observed trend in the semiconductor industry, states that the number of transistors on a microchip doubles approximately every two years. This exponential growth in computing power has fueled remarkable technological advancements across various sectors, including communication, healthcare, and entertainment. Understanding exponential trends allows us to anticipate future technological capabilities and plan for their societal impact.
4. Viral Spread: The spread of infectious diseases, especially those transmitted through close contact, can often be modeled using exponential functions. Each infected individual can potentially infect several others, leading to an exponential increase in the number of cases. This understanding is crucial for public health officials to implement effective containment strategies and minimize the impact of outbreaks.
5. Radioactive Decay: While the expression (2x)³ describes growth, the principle of exponential growth also applies to decay. Radioactive decay, where unstable atomic nuclei lose energy, follows an exponential decline. The half-life, the time it takes for half the substance to decay, is a key concept related to this exponential decay. Understanding exponential decay is essential in fields like nuclear physics and environmental science.
Deeper Dive: Mathematical Modeling and its Significance
The expression (2x)³ acts as a building block for more complex mathematical models that describe exponential growth and decay. These models often incorporate additional factors like limiting resources, carrying capacity, or external influences. For instance, in population modeling, logistic growth models account for limitations in resources, which cause the exponential growth to eventually plateau.
These models are not merely theoretical exercises; they're critical tools used to make predictions, optimize resource allocation, and understand complex systems. By understanding the underlying mathematical principles, we can improve our ability to analyze and interpret data, make informed decisions, and solve real-world problems.
Beyond (2x)³: Exploring Variations and Generalizations
While we've focused on (2x)³, the principles discussed extend to other similar expressions. For example, (ax)ⁿ represents exponential growth where 'a' is the base and 'n' is the exponent. Understanding the effect of changing 'a' and 'n' is crucial for adapting models to specific contexts. A larger 'a' leads to faster growth, and a larger 'n' increases the overall magnitude of the exponential effect.
Furthermore, the concept extends beyond simple exponential functions. Many real-world phenomena are better described by more intricate models that incorporate multiple exponential terms, or variations like power-law functions. These models can capture more nuanced behaviors and provide even more accurate representations of reality.
Frequently Asked Questions (FAQ)
Q1: What happens if x is negative?
A1: If x is negative, the expression (2x)³ will still be calculated, but the result will also be negative. The sign of the result will depend on whether the exponent is even or odd. In this case, with an odd exponent (3), the result will be negative. This indicates a decreasing value, relevant in contexts like modeling decay processes.
Q2: Can this expression be used to model everything that grows rapidly?
A2: While (2x)³ and similar expressions capture the essence of exponential growth, they are simplifications. Many real-world systems exhibit more complex growth patterns affected by various factors. More sophisticated models are needed to accurately represent these systems' intricate dynamics. However, understanding basic exponential growth is crucial as a foundation for more complex models.
Q3: How can I apply this knowledge practically?
A3: The practical application depends on your field. If you're in finance, understanding compound interest is key. In biology, it's about population modeling and growth rates. In computer science, it relates to algorithmic efficiency and scaling. The core principle is recognizing exponential trends and using appropriate models to analyze and predict future outcomes.
Q4: Are there limitations to exponential growth models?
A4: Yes, exponential growth models are not universally applicable. Real-world systems are often constrained by resources, competition, or other limiting factors. Pure exponential growth can only persist for a limited time before these constraints come into play, leading to a deviation from the purely exponential pattern. This is why more realistic models, like logistic growth models, are often used.
Conclusion: Embracing the Power of Exponential Growth
The seemingly simple expression "2x x 2x x 2x," ultimately represented as 8x³, provides a fundamental understanding of exponential growth. This concept is not just a mathematical curiosity; it's a powerful tool for understanding and modeling a wide array of phenomena across various disciplines. By grasping the underlying principles and recognizing its real-world applications, we can gain valuable insights, make informed decisions, and contribute to progress in countless fields. From understanding population dynamics to anticipating technological advancements, the implications of exponential growth are far-reaching and continue to shape our world. This understanding empowers us to navigate the complexities of the rapidly changing world around us and participate actively in its future.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2x X 2x X 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.