3 4 5 X 2
plugunplug
Sep 17, 2025 · 6 min read
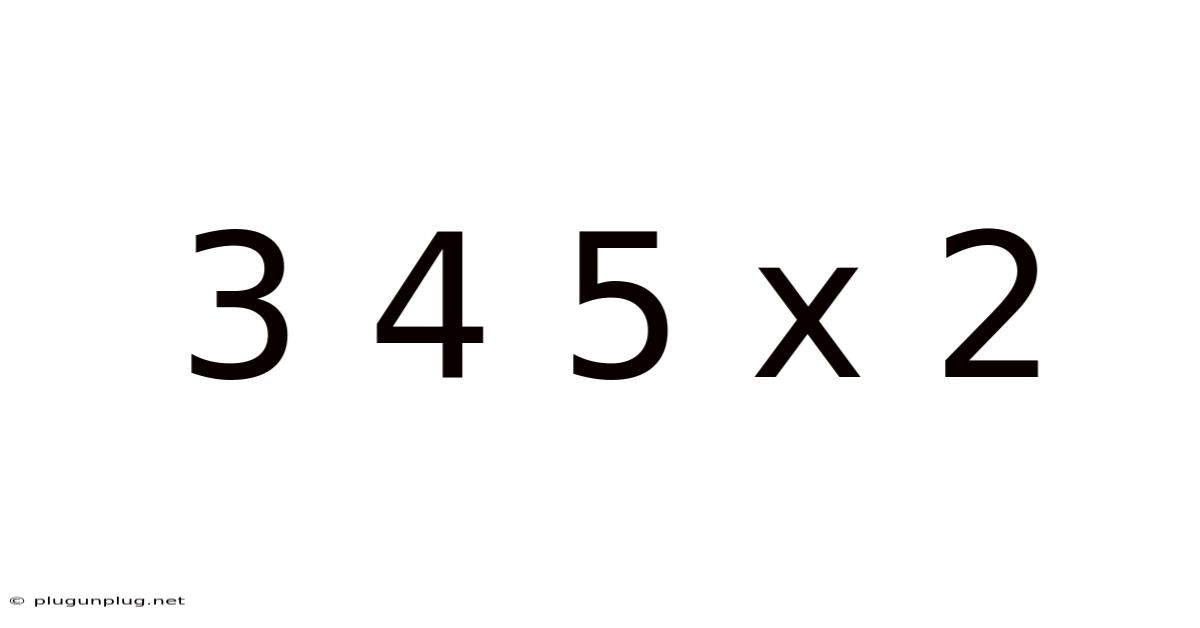
Table of Contents
Decoding 3 4 5 x 2: Exploring Multiplication, Geometry, and Problem-Solving
This article delves into the seemingly simple mathematical expression "3 4 5 x 2," exploring its implications beyond basic multiplication. We'll unpack the arithmetic, examine its geometric representation, and investigate how this expression can be used to solve various problems, demonstrating its relevance in different mathematical contexts. Understanding this expression provides a foundation for grasping more complex concepts in arithmetic, geometry, and beyond. This exploration will cater to a broad audience, from students needing a refresher to those curious about the underlying principles of mathematics.
Understanding the Arithmetic: Basic Multiplication
At its core, "3 4 5 x 2" represents a series of multiplications. However, the lack of explicit operators necessitates an interpretation. The most straightforward interpretation is to treat it as a single number, 345, multiplied by 2. This gives us a simple arithmetic problem:
345 x 2 = 690
This is a straightforward application of multiplication, a fundamental operation in arithmetic. It highlights the importance of understanding place value and the distributive property. To solve this mentally or on paper, we can break down the multiplication:
- 2 x 5 = 10 (write down 0, carry-over 1)
- 2 x 4 = 8 + 1 (carry-over) = 9 (write down 9)
- 2 x 3 = 6 (write down 6)
This results in the final answer: 690. This seemingly simple calculation forms the basis for understanding more complex mathematical operations.
The Geometric Interpretation: Areas and Scaling
Beyond the arithmetic, the expression can be interpreted geometrically. Let's consider the number 345 as representing an area. Imagine a rectangle with sides of length 34.5 units and 10 units. The area of this rectangle would be 345 square units.
Multiplying this by 2 can be visualized in two ways:
-
Doubling the length: We can double the length of one side (e.g., 34.5 units becomes 69 units), keeping the other side (10 units) constant. The new rectangle would have an area of 690 square units. This represents scaling the original rectangle.
-
Creating a duplicate: We can create an identical rectangle next to the original one. Now we have two rectangles, each with an area of 345 square units, for a total area of 690 square units. This approach emphasizes the concept of multiplication as repeated addition.
This geometric visualization provides a concrete representation of the multiplication problem, making it easier to grasp the concept, particularly for visual learners. This approach bridges the gap between abstract numerical operations and tangible geometric shapes.
Exploring Variations and Ambiguity: Order of Operations
While the most common interpretation treats "3 4 5" as a single number, the lack of explicit operators introduces potential ambiguity. Let's consider alternative interpretations, although less likely given standard mathematical notation:
-
(3 x 4) x (5 x 2): This interpretation follows the order of operations (PEMDAS/BODMAS), prioritizing multiplication. This would yield (12) x (10) = 120. This interpretation is less probable because it requires significant deviation from typical numerical representation.
-
3 x 4 x 5 x 2: This interpretation is equally valid, resulting in 120. This demonstrates the importance of precise notation in mathematics.
The ambiguity underscores the critical role of clear and unambiguous notation in mathematical expressions. The absence of explicit operators leads to multiple interpretations, highlighting the necessity of standard mathematical conventions to avoid confusion.
Problem-Solving Applications: Real-World Examples
The "3 4 5 x 2" expression, even in its simple form, can be applied to various real-world problems. Let's explore some examples:
-
Inventory Management: A warehouse has 345 boxes of a certain product. If they receive a duplicate shipment of the same size, how many boxes do they have in total? This directly translates to 345 x 2 = 690 boxes.
-
Construction and Measurement: A contractor needs to calculate the total length of fencing required for a rectangular area twice the size of a given area. If the original area has dimensions represented by 34.5 units and 10 units, the total length needed for the doubled area is represented by the solution to 345 x 2.
-
Financial Calculations: A company's profit for a quarter is 345 thousand dollars. If they expect to double their profit in the next quarter, what would their total profit be for both quarters? This again demonstrates the practical application of this simple multiplication.
These real-world examples highlight the practical applicability of this seemingly simple mathematical expression in various domains. The ability to translate a word problem into a mathematical expression and solve it is a crucial skill.
Extending the Concept: Factors and Multiples
The number 690, the result of 345 x 2, possesses several mathematical properties worth exploring. Understanding its factors and multiples can provide further insights:
-
Factors of 690: The factors of 690 are the numbers that divide evenly into 690. These include 1, 2, 3, 5, 6, 10, 15, 23, 30, 46, 69, 115, 138, 230, 345, and 690. Understanding factors is crucial in simplifying fractions and solving equations.
-
Multiples of 690: The multiples of 690 are the numbers obtained by multiplying 690 by other integers. These include 690, 1380, 2070, 2760, and so on. Understanding multiples helps in solving problems related to patterns and sequences.
Exploring the factors and multiples of 690 enhances our understanding of number theory and lays the foundation for more advanced mathematical concepts.
Expanding on the 3-4-5 Triangle: Pythagorean Triples
The numbers 3, 4, and 5 are well-known as a Pythagorean triple. This means they satisfy the Pythagorean theorem (a² + b² = c²), where a and b are the lengths of the legs of a right-angled triangle, and c is the length of the hypotenuse. In this case, 3² + 4² = 9 + 16 = 25 = 5².
While the initial expression doesn't explicitly involve this relationship, it indirectly connects to the concept of scaling and geometric transformations. Multiplying the sides of a 3-4-5 triangle by 2 results in a similar triangle with sides 6-8-10, still maintaining the Pythagorean relationship. This demonstrates the preservation of geometric properties under scaling transformations.
Frequently Asked Questions (FAQ)
Q: What if the expression was written as 3 x 4 x 5 x 2? Would the answer be different?
A: Yes, the answer would be different. In this case, following the order of operations, we'd have 3 x 4 x 5 x 2 = 120. This highlights the importance of precise notation.
Q: How can I use this concept in everyday life?
A: This simple multiplication is used constantly in everyday life, from calculating the cost of multiple items to determining the area of a room.
Q: Are there other Pythagorean triples besides 3-4-5?
A: Yes, there are infinitely many Pythagorean triples. Some examples include 5-12-13 and 7-24-25.
Conclusion: Beyond the Numbers
The seemingly simple expression "3 4 5 x 2" reveals a surprising depth when explored beyond basic arithmetic. We've moved from basic multiplication to geometric interpretations, exploring the concepts of scaling and area. We’ve touched upon the ambiguity of notation, the practical application in problem-solving, and even the intriguing world of Pythagorean triples. This exploration emphasizes the interconnectedness of different mathematical concepts and the importance of understanding the underlying principles rather than just memorizing procedures. By analyzing this seemingly simple expression, we've gained a deeper appreciation for the power and elegance of mathematics. The journey from a basic calculation to understanding its geometric and numerical implications underscores the richness and complexity hidden within even the simplest mathematical expressions. This exploration should empower you to approach future mathematical challenges with a more profound understanding and a greater appreciation for the underlying principles.
Latest Posts
Latest Posts
-
Organs In The Abdominal Cavity
Sep 17, 2025
-
What Is Penetration Pricing Strategy
Sep 17, 2025
-
Bubble Skin Care For Kids
Sep 17, 2025
-
All The Factors For 26
Sep 17, 2025
-
Bond Angle Of Trigonal Pyramidal
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 4 5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.