3 X 5 X 2
plugunplug
Sep 20, 2025 · 6 min read
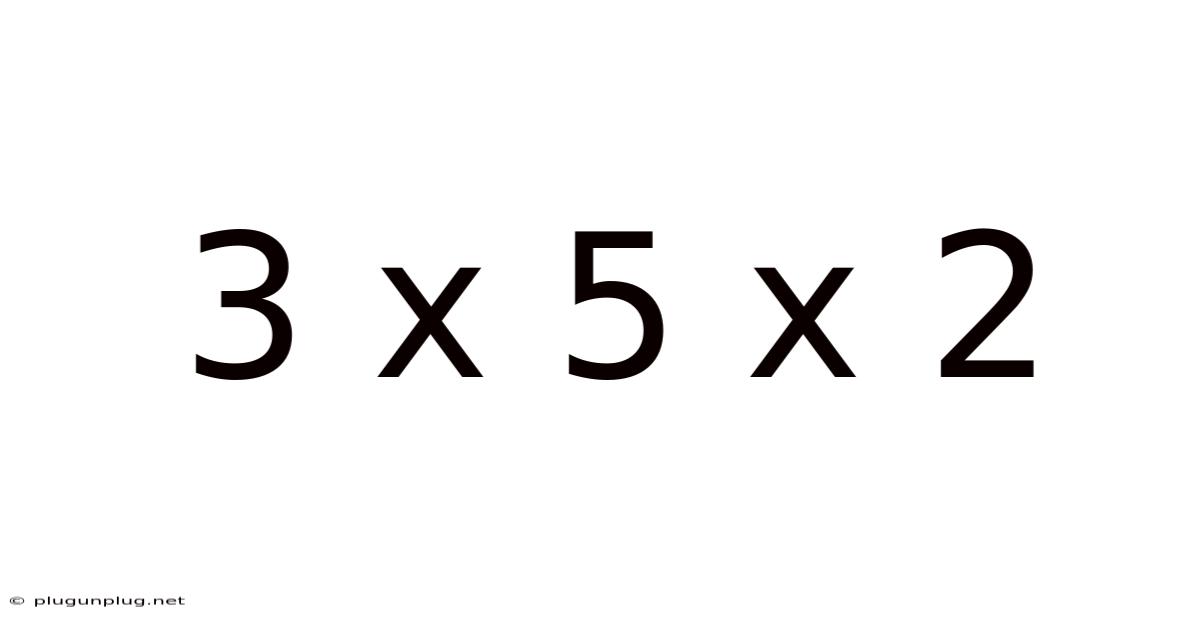
Table of Contents
Decoding 3 x 5 x 2: Exploring Dimensions, Volume, and Applications
This seemingly simple mathematical expression, 3 x 5 x 2, opens a gateway to understanding fundamental concepts in geometry, spatial reasoning, and practical applications across various fields. This article will delve into the meaning of this expression, exploring its implications in calculating volume, visualizing three-dimensional shapes, and highlighting its relevance in diverse real-world scenarios. We'll cover everything from basic calculations to more complex applications, ensuring a comprehensive understanding for readers of all levels.
Understanding the Basics: Multiplication and Dimensions
At its core, "3 x 5 x 2" represents a multiplication problem. In a geometric context, this signifies the multiplication of three dimensions: length, width, and height. Each number represents the measurement of one of these dimensions. Let's assume we're dealing with measurements in centimeters (cm):
- 3 cm: This could represent the length of an object.
- 5 cm: This could represent the width of an object.
- 2 cm: This could represent the height of an object.
The multiplication, 3 x 5 x 2, gives us the volume of a rectangular prism (also known as a cuboid). This is a three-dimensional shape with six rectangular faces. Think of a shoebox, a brick, or even a building block – these are all examples of rectangular prisms.
Calculating the Volume: A Step-by-Step Guide
To calculate the volume, we simply multiply the three dimensions together:
3 cm x 5 cm x 2 cm = 30 cubic centimeters (cm³)
The unit "cubic centimeters" (cm³) signifies that we are measuring volume – the amount of three-dimensional space occupied by the object. It's crucial to remember to always include the appropriate units when expressing volume. If the dimensions were in meters (m), the volume would be expressed in cubic meters (m³), and so on.
Visualizing the Shape: From Numbers to Reality
It's helpful to visualize the shape represented by these dimensions. Imagine a rectangular box. One side measures 3 cm, another 5 cm, and the height is 2 cm. You can draw this box on paper, or even better, use physical objects like building blocks to construct a model. This hands-on approach significantly aids comprehension, particularly for visual learners.
Exploring Variations and Applications: Beyond the Basic Cuboid
While the initial example uses a rectangular prism, the principle of multiplying three dimensions to find volume applies to numerous situations:
-
Irregular Shapes: While calculating the volume of irregular shapes can be more complex and might involve calculus, the fundamental concept remains the same. Breaking down a complex shape into simpler rectangular prisms can provide an approximation of its volume.
-
Packaging and Shipping: Companies use these calculations extensively when designing packaging for their products. They need to ensure the package is large enough to accommodate the product while minimizing wasted space and shipping costs. The dimensions 3 x 5 x 2 could represent the internal dimensions of a box designed for a particular item.
-
Construction and Engineering: Architects and engineers use similar calculations to determine the volume of materials required for construction projects. For instance, the volume of concrete needed for a foundation could be estimated using this approach, factoring in length, width, and depth.
-
Data Storage: In the digital world, data storage is often expressed in terms of volume. While not directly related to physical dimensions, the concept remains relevant in terms of capacity and organization. Think of a 3D array in computer science where data is structured across multiple dimensions.
-
Scientific Applications: Scientists use volume calculations in numerous fields, including chemistry (measuring liquid volumes), biology (calculating cell sizes), and physics (analyzing fluid dynamics).
Advanced Concepts: Scaling and Ratio
The expression 3 x 5 x 2 allows us to explore concepts such as scaling and ratio. If we were to double all dimensions (6 x 10 x 4), the resulting volume would be eight times larger (240 cm³). This demonstrates the exponential relationship between dimensions and volume. Similarly, if we were to halve all dimensions (1.5 x 2.5 x 1), the resulting volume would be one-eighth the original (3.75 cm³). Understanding this relationship is crucial in various applications, from designing models to scaling up industrial processes.
Connecting to Real-World Scenarios: Examples
Let’s consider a few specific examples to demonstrate the practical applications of understanding 3 x 5 x 2:
Example 1: Aquarium Design: You're designing a small aquarium for your betta fish. You decide that the tank should have internal dimensions of 30 cm (length), 15 cm (width), and 10 cm (height). What is the volume of water the tank can hold? Here, we can simplify the dimensions: 3 x 1.5 x 1, resulting in a volume of 4.5 cubic centimeters. However, we’d need to convert the cm into cubic meters (remember, 100cm = 1 meter), then multiply by 1000 to convert cubic centimeters to cubic meters. The larger the tank, the more complex these calculations become.
Example 2: Concrete Slab: A contractor needs to pour a concrete slab for a small patio. The slab needs to be 3 meters long, 5 meters wide, and 0.2 meters thick. What is the volume of concrete required? This would be 3 m x 5 m x 0.2 m = 3 cubic meters of concrete.
Example 3: Packing Boxes: You're moving house and need to pack books into boxes. Each box has internal dimensions of 30 cm, 50 cm, and 20 cm. If you have 100 books, and each book occupies approximately 100 cubic centimeters of space, will one box suffice? Let's calculate the volume of the box: 30cm x 50cm x 20cm = 30000 cubic centimeters. Given that you have 100 books requiring 10,000 cubic centimeters, one box is definitely big enough to hold all of your books, provided the books fit well.
Frequently Asked Questions (FAQ)
Q: What if the dimensions are not whole numbers?
A: The calculation remains the same. You simply multiply the decimal numbers together. For example, 3.5 x 5.2 x 2.1 = 36.4 cubic units.
Q: What are some other units of volume?
A: Common units of volume include cubic meters (m³), cubic centimeters (cm³), cubic millimeters (mm³), liters (L), gallons (gal), and cubic feet (ft³). The appropriate unit depends on the context.
Q: Can this calculation be used for shapes other than rectangular prisms?
A: While the direct multiplication is specific to rectangular prisms, the underlying concept of multiplying dimensions to find volume applies to other shapes. However, the formulas for calculating volume become more complex for shapes like spheres, cylinders, and pyramids.
Q: How does this relate to surface area?
A: Surface area refers to the total area of the faces of a three-dimensional object. It's calculated differently from volume. While volume gives the space inside, surface area is the area of the exterior. You would use different formulas to calculate surface area than for volume.
Conclusion: The Enduring Relevance of 3 x 5 x 2
The seemingly simple expression, 3 x 5 x 2, serves as a gateway to understanding fundamental concepts in mathematics and geometry. From calculating the volume of a simple rectangular prism to tackling more complex real-world problems, the ability to visualize and manipulate three-dimensional shapes is invaluable. This understanding extends to various fields, highlighting the enduring relevance of this seemingly simple calculation in diverse and dynamic applications. The power of this fundamental principle lies not just in the answer (30 cubic units), but in the underlying understanding of spatial reasoning and dimensional relationships. This knowledge builds a strong foundation for tackling more advanced mathematical and scientific concepts in the future.
Latest Posts
Latest Posts
-
How To Multiply Standard Form
Sep 20, 2025
-
Use Avarice In A Sentence
Sep 20, 2025
-
Difference Between Teepee And Wigwam
Sep 20, 2025
-
Why Sand Is Called Sand
Sep 20, 2025
-
Conversion Factor Meters To Miles
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 X 5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.