33 50 As A Percent
plugunplug
Sep 20, 2025 · 5 min read
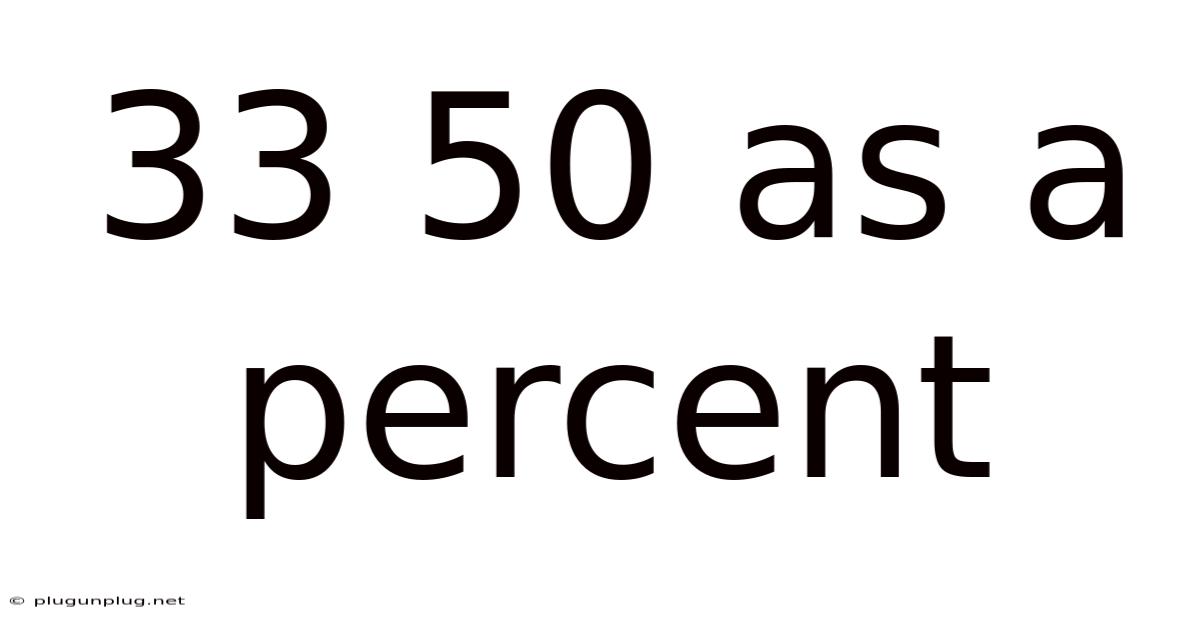
Table of Contents
Decoding 33/50 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article delves into the process of converting fractions to percentages, focusing specifically on the fraction 33/50 and exploring its various interpretations and practical applications. We’ll move beyond a simple calculation to understand the underlying principles and provide you with a robust understanding of this common mathematical concept.
Understanding Fractions and Percentages
Before we dive into converting 33/50 to a percentage, let's briefly review the fundamentals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion or rate per hundred. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. The key link between fractions and percentages is that both express proportions. Converting a fraction to a percentage involves finding its equivalent fraction with a denominator of 100.
Converting 33/50 to a Percentage: The Step-by-Step Process
There are two primary methods for converting 33/50 to a percentage:
Method 1: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the fundamental principle of equivalent fractions. To change the denominator from 50 to 100, we multiply it by 2. To maintain the equality of the fraction, we must also multiply the numerator by the same factor.
- Multiply the denominator by 2: 50 * 2 = 100
- Multiply the numerator by 2: 33 * 2 = 66
- The equivalent fraction is: 66/100
Since a percentage is a fraction out of 100, 66/100 is equal to 66%.
Method 2: Using Decimal Conversion
This method involves first converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
- Divide the numerator by the denominator: 33 ÷ 50 = 0.66
- Multiply the decimal by 100: 0.66 * 100 = 66
- Add the percentage symbol: 66%
Therefore, using both methods, we confirm that 33/50 is equivalent to 66%.
Practical Applications of 33/50 (66%)
Understanding how to convert fractions like 33/50 to percentages has numerous practical applications in various fields:
-
Academic Assessments: If a student answered 33 out of 50 questions correctly on a test, their score would be 66%. This allows for easy comparison of performance across different tests and students.
-
Sales and Discounts: A store offering a 33/50 discount on an item is essentially offering a 66% discount. This helps consumers quickly understand the savings involved.
-
Financial Analysis: In finance, percentages are crucial for expressing things like interest rates, profit margins, and return on investment. Understanding fraction-to-percentage conversion is essential for interpreting financial data.
-
Data Analysis and Statistics: Percentages are widely used to represent proportions and probabilities in statistical analysis. Converting fractions to percentages helps in visualizing and interpreting data more effectively.
-
Everyday Life: From calculating tips at restaurants to determining the percentage of ingredients in a recipe, percentage calculations are ubiquitous in our daily lives. The ability to convert fractions to percentages simplifies many everyday tasks.
Beyond the Calculation: Exploring Related Concepts
While the conversion of 33/50 to 66% is straightforward, exploring related concepts enhances our understanding of percentages and their applications:
-
Percentage Increase and Decrease: Suppose a value increases from 50 to 83. To calculate the percentage increase, we first find the difference (83 - 50 = 33), then divide this difference by the original value (33/50), and finally multiply by 100 to get the percentage increase (66%). Similarly, we can calculate percentage decreases.
-
Proportions and Ratios: Percentages are closely related to proportions and ratios. A ratio of 33:50 is equivalent to the fraction 33/50 and the percentage 66%. Understanding this relationship allows for flexible problem-solving in various scenarios.
-
Understanding Decimal Places and Rounding: In some cases, the decimal representation of a fraction might not be exact. For instance, 1/3 is approximately 0.3333..., and its percentage equivalent is approximately 33.33%. Knowing how to handle decimal places and rounding is crucial for accurate calculations.
-
Working with Percentages Greater Than 100%: It's possible to have percentages greater than 100%, representing values exceeding the original whole. For example, if a quantity increases from 50 to 165, the percentage increase is 230% ((165-50)/50 * 100).
Frequently Asked Questions (FAQ)
-
Q: How do I convert any fraction to a percentage?
A: Divide the numerator by the denominator to obtain a decimal. Then, multiply the decimal by 100 and add the percentage symbol (%).
-
Q: What if the fraction results in a repeating decimal when converted to a percentage?
A: You can either round the decimal to a reasonable number of decimal places or express the percentage as a fraction with a denominator of 100 (or 1000, etc.).
-
Q: Are there any shortcuts for converting fractions to percentages?
A: Some common fractions have easily memorized percentage equivalents (e.g., 1/2 = 50%, 1/4 = 25%, 1/5 = 20%). However, the general methods described above are applicable to any fraction.
-
Q: Why are percentages useful?
A: Percentages provide a standardized way to compare proportions and rates across different contexts. They make it easier to understand and interpret data, making them essential in various fields.
Conclusion
Converting 33/50 to a percentage, resulting in 66%, is a simple yet fundamental mathematical operation with far-reaching applications. This article has explored the methods, practical implications, and related concepts to provide a comprehensive understanding of this important skill. Mastering fraction-to-percentage conversion empowers you to confidently tackle various numerical challenges in your academic pursuits, professional life, and everyday activities. Remember that the key lies not only in performing the calculation accurately but also in understanding the underlying principles and applying this knowledge to real-world situations. By strengthening your understanding of percentages, you are equipping yourself with a valuable tool for navigating the numerical world around us.
Latest Posts
Latest Posts
-
Difference Between Village And Hamlet
Sep 20, 2025
-
How To Find Enthalpy Change
Sep 20, 2025
-
88 Degrees Celsius To Fahrenheit
Sep 20, 2025
-
Define Unremarkable In Medical Terms
Sep 20, 2025
-
How Many Bones In Foot
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 33 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.