36 50 As A Percent
plugunplug
Sep 21, 2025 · 5 min read
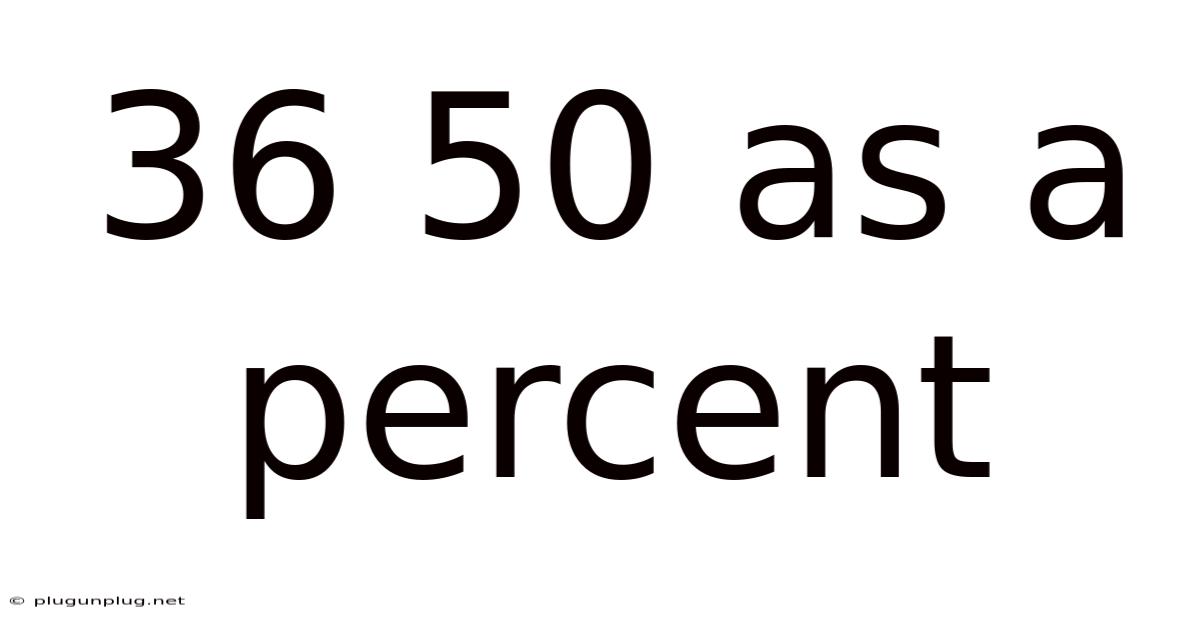
Table of Contents
Understanding 36/50 as a Percentage: A Comprehensive Guide
What does 36 out of 50 represent as a percentage? This seemingly simple question touches upon fundamental concepts in mathematics, particularly fractions, decimals, and percentages – skills crucial for everyday life, academic pursuits, and professional success. This comprehensive guide will not only answer this question but also delve deeper into the underlying principles, providing you with a thorough understanding of percentage calculations and their practical applications. We'll explore different methods for solving this problem, address common misconceptions, and provide further examples to solidify your grasp of this important mathematical concept.
Understanding Fractions, Decimals, and Percentages
Before we tackle 36/50 as a percentage, let's establish a solid foundation by understanding the relationship between fractions, decimals, and percentages.
-
Fractions: A fraction represents a part of a whole. It is expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). In our case, 36/50 is a fraction where 36 represents the part and 50 represents the whole.
-
Decimals: A decimal is another way to represent a part of a whole. It uses a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on.
-
Percentages: A percentage represents a fraction or decimal as a proportion of 100. The symbol "%" signifies "per hundred." For example, 50% means 50 out of 100, or 50/100.
Method 1: Direct Conversion from Fraction to Percentage
The most straightforward way to convert 36/50 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (36) by the denominator (50). 36 ÷ 50 = 0.72
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.72 × 100 = 72%
Therefore, 36/50 is equal to 72%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction with a denominator of 100. This method is particularly helpful for fractions with denominators that are factors of 100.
Since 50 is a factor of 100 (100 ÷ 50 = 2), we can easily convert 36/50 to an equivalent fraction with a denominator of 100:
- Multiply both the numerator and the denominator by 2: (36 × 2) / (50 × 2) = 72/100
Since 72/100 means 72 out of 100, this directly translates to 72%.
Method 3: Using Proportions
The concept of proportions provides another effective way to solve this problem. A proportion is a statement that two ratios are equal. We can set up a proportion to find the percentage:
- Let 'x' represent the percentage we want to find.
- We can set up the proportion: 36/50 = x/100
To solve for 'x', we can cross-multiply:
- 50x = 3600
- x = 3600 ÷ 50
- x = 72
Therefore, 36/50 is equal to 72%.
Illustrative Examples and Applications
Let's explore some real-world scenarios where understanding 36/50 as 72% can be useful:
-
Academic Performance: If a student answered 36 out of 50 questions correctly on a test, their score is 72%. This helps to easily assess their performance relative to the total possible score.
-
Sales and Marketing: If a company aimed to sell 50 units of a product and sold 36, their sales achievement is 72%. This data is crucial for evaluating sales targets and strategies.
-
Survey Results: If 36 out of 50 respondents to a survey answered "yes" to a particular question, the percentage of "yes" responses is 72%. This allows for easy interpretation and analysis of survey data.
-
Financial Calculations: Understanding percentages is crucial for calculating interest rates, discounts, profit margins, and other financial aspects. For instance, if you invested $50 and earned a profit of $36, your return on investment is 72%.
Addressing Common Misconceptions
-
Confusing numerator and denominator: Remember that the numerator represents the part, and the denominator represents the whole. Incorrectly switching these will lead to an incorrect percentage.
-
Incorrect decimal-to-percentage conversion: Always multiply the decimal by 100 to convert it to a percentage. Forgetting this step will lead to a wrong answer.
-
Overcomplicating the calculations: While multiple methods exist, choose the method you find most comfortable and efficient. Don't overthink the process.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve this problem?
A1: Yes, a calculator can simplify the process, especially for more complex fraction-to-percentage conversions. Simply divide the numerator by the denominator and then multiply the result by 100.
Q2: What if the fraction has a larger denominator that isn't easily converted to 100?
A2: The direct conversion method (dividing the numerator by the denominator and multiplying by 100) works for any fraction, regardless of the denominator's size.
Q3: Are there any online tools or websites that can help with percentage calculations?
A3: Yes, many online calculators and websites are available to help with percentage calculations. These tools can be particularly helpful for checking your work or solving more complex percentage problems.
Q4: How can I improve my understanding of percentages?
A4: Practice is key! Work through various examples, try different methods, and apply percentage calculations to real-world scenarios.
Conclusion
Converting 36/50 to a percentage is a straightforward process with multiple approaches. Understanding these methods is crucial not only for solving specific problems but also for developing a solid grasp of fundamental mathematical concepts. This knowledge empowers you to tackle various real-world applications, from analyzing academic performance to understanding financial data. Remember to practice regularly to build confidence and proficiency in percentage calculations. By mastering these concepts, you enhance your problem-solving skills and improve your overall mathematical literacy. This understanding is invaluable in numerous academic and professional contexts, making it a vital skill to develop.
Latest Posts
Latest Posts
-
Crossword Clue Spicy Indian Dish
Sep 21, 2025
-
How Do I Round Numbers
Sep 21, 2025
-
Natures First Green Is Gold
Sep 21, 2025
-
Convert 10 Pounds To Kilograms
Sep 21, 2025
-
1900 Was A Leap Year
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 36 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.