4 2 X 4 2
plugunplug
Sep 18, 2025 · 5 min read
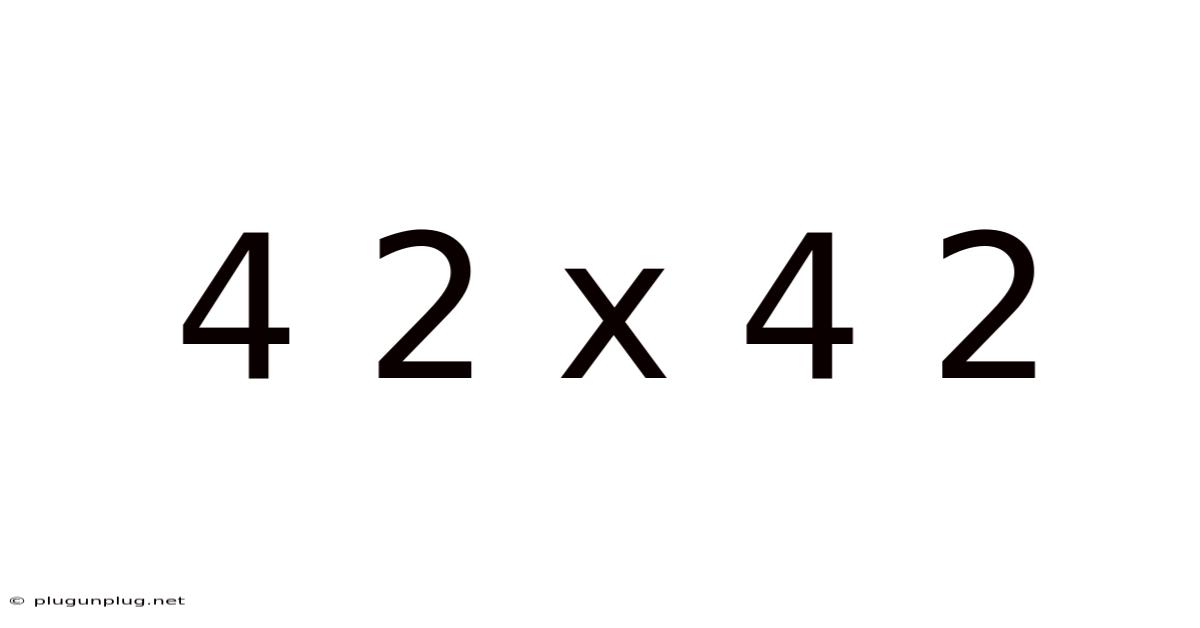
Table of Contents
Decoding 4² x 4²: A Deep Dive into Exponents and Area Calculation
This article explores the mathematical expression 4² x 4², breaking down its components, explaining the underlying principles of exponents and area calculation, and demonstrating its practical applications. We'll delve into the step-by-step process of solving this equation and address common misconceptions, making this a comprehensive guide for anyone seeking a thorough understanding of this seemingly simple mathematical problem. Understanding 4² x 4² provides a strong foundation for more complex algebraic manipulations and geometrical problem-solving.
Understanding Exponents
The core of the expression 4² x 4² lies in understanding exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In 4², the '4' is the base and the '2' is the exponent. This means 4² is equivalent to 4 x 4. Therefore, 4² = 16.
Let's break down the individual components of our equation:
- 4²: This means 4 multiplied by itself twice (4 x 4 = 16).
- 4² x 4²: This means we're multiplying the result of 4² (which is 16) by itself again (16 x 16).
Step-by-Step Calculation of 4² x 4²
-
Calculate each exponent: First, we calculate each 4². As established above, 4² = 16.
-
Multiply the results: Next, we multiply the results of the exponent calculations together: 16 x 16 = 256.
Therefore, 4² x 4² = 256.
The Laws of Exponents
The calculation above can also be simplified using the laws of exponents. Specifically, the product of powers rule states that when multiplying two numbers with the same base, you can add their exponents.
In our case, we have 4² x 4². Since both terms have the same base (4), we can rewrite the equation as:
4² x 4² = 4⁽²⁺²⁾ = 4⁴
Now, we calculate 4⁴:
4⁴ = 4 x 4 x 4 x 4 = 256
This demonstrates the efficiency of understanding and applying the laws of exponents. It simplifies calculations and provides a more elegant solution, especially when dealing with larger exponents or more complex expressions.
Geometric Interpretation: Area of a Square
The expression 4² x 4² can be visualized geometrically. Consider two squares.
-
The first square: Has sides of length 4 units. Its area is calculated as side x side = 4 x 4 = 4² = 16 square units.
-
The second square: Also has sides of length 4 units. Its area is also 4² = 16 square units.
The expression 4² x 4² represents the area of a larger rectangle formed by placing these two squares side-by-side. The rectangle has dimensions of 16 units by 16 units. Therefore, its area is 16 x 16 = 256 square units. This provides a visual representation of the mathematical calculation, grounding the abstract concept in a tangible reality.
Expanding the Concept: Higher Exponents and Different Bases
The principles discussed above can be applied to a wide range of problems involving exponents and area calculations. Let's consider some examples:
-
Higher Exponents: If we had 4³ x 4³, we would first calculate each exponent (4³ = 4 x 4 x 4 = 64) and then multiply the results (64 x 64 = 4096). Alternatively, using the product of powers rule: 4³ x 4³ = 4⁶ = 4096.
-
Different Bases: The same principles apply to expressions with different bases. For example, 5² x 5² = 25 x 25 = 625, or using the product of powers rule: 5² x 5² = 5⁴ = 625.
-
Mixed Operations: More complex problems might involve multiple operations. For example, (3² + 2²) x 4² would be solved by calculating the exponents first (3²=9, 2²=4, 4²=16), then performing the addition (9+4=13), and finally the multiplication (13 x 16 = 208). Order of operations (PEMDAS/BODMAS) should always be followed.
Real-World Applications
Understanding exponents and area calculations has numerous practical applications across various fields:
-
Engineering: Calculating the volume of cubes or rectangular prisms, determining the surface area of objects.
-
Construction: Calculating the amount of materials needed for projects, determining the area of rooms or plots of land.
-
Computer Science: Calculating data storage capacity, determining the complexity of algorithms.
-
Finance: Calculating compound interest, understanding exponential growth and decay.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 4² and 2⁴?
-
A: 4² means 4 x 4 = 16, while 2⁴ means 2 x 2 x 2 x 2 = 16. While they have the same result in this case, this is coincidental. They represent different mathematical expressions.
-
Q: Can I always add the exponents when multiplying numbers with the same base?
-
A: Yes, this is a fundamental law of exponents. The product of powers rule states: aᵐ x aⁿ = a⁽ᵐ⁺ⁿ⁾ where 'a' is the base, and 'm' and 'n' are the exponents.
-
Q: What if the bases are different?
-
A: If the bases are different, you cannot directly add the exponents. You must calculate each exponent separately and then perform the multiplication. For example, 2² x 3² = 4 x 9 = 36.
-
Q: How can I visualize 4³ x 4³?
-
A: You can visualize this as the volume of a cube with sides of length 64 units (since 4³ = 64). The expression 4³ x 4³ represents the volume of a larger cube formed by arranging these smaller cubes.
Conclusion
The seemingly simple expression 4² x 4² provides a gateway to understanding fundamental mathematical concepts such as exponents and area calculations. By breaking down the problem step-by-step, applying the laws of exponents, and visualizing the geometric interpretation, we can appreciate its significance beyond a simple numerical calculation. The ability to solve this type of problem is crucial for a solid foundation in mathematics and its applications in various fields, highlighting the importance of understanding these core principles. Mastering these concepts unlocks a deeper understanding of more complex mathematical problems and allows for efficient and accurate problem-solving in a variety of contexts. The ability to manipulate and interpret such expressions lays the groundwork for further mathematical explorations and applications in the real world.
Latest Posts
Latest Posts
-
A Piece Of Your Mind
Sep 18, 2025
-
How Many Circles Of Hell
Sep 18, 2025
-
My Very Educated Mother Planets
Sep 18, 2025
-
50 Degree Fahrenheit To Celsius
Sep 18, 2025
-
When Was Skara Brae Discovered
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 4 2 X 4 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.