4 X 3 X 4
plugunplug
Sep 17, 2025 · 6 min read
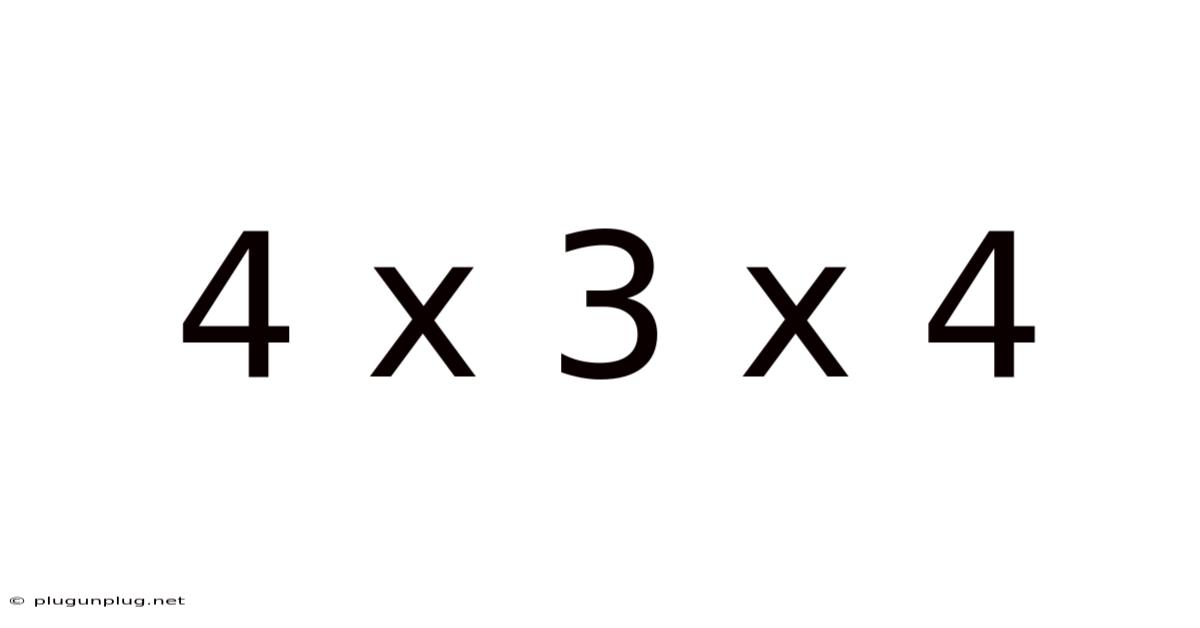
Table of Contents
Decoding 4 x 3 x 4: A Deep Dive into Multiplication and its Applications
This article delves into the seemingly simple mathematical expression "4 x 3 x 4," exploring its basic calculation, its underlying principles of multiplication, and its broader applications across various fields. We will unpack the concept of multiplication, examine different approaches to solving this equation, and discuss how this fundamental operation forms the basis for more complex mathematical concepts and real-world problems. This exploration will cater to various levels of understanding, from beginners grasping the fundamentals of arithmetic to those seeking a deeper appreciation of its significance.
Understanding the Fundamentals: What is Multiplication?
Before we tackle 4 x 3 x 4, let's solidify our understanding of multiplication itself. Multiplication is essentially a shortcut for repeated addition. When we say 4 x 3, we are essentially saying "add four to itself three times" (4 + 4 + 4 = 12). It represents the process of combining equal groups of items. The number being multiplied (in this case, 4) is called the multiplicand, the number by which we are multiplying (3) is the multiplier, and the result (12) is the product.
In our expression, 4 x 3 x 4, we have three numbers involved in a series of multiplications. This is known as a chained multiplication or a product of multiple factors. The order in which we perform these multiplications doesn't change the final answer, thanks to the commutative property of multiplication, which states that the order of the factors does not affect the product (a x b = b x a).
Calculating 4 x 3 x 4: Different Approaches
There are several ways to approach calculating 4 x 3 x 4:
1. Sequential Multiplication: This involves performing the multiplications one after the other, from left to right or right to left.
- Left to Right: (4 x 3) x 4 = 12 x 4 = 48
- Right to Left: 4 x (3 x 4) = 4 x 12 = 48
As demonstrated, both methods yield the same result, highlighting the commutative property in action.
2. Using the Associative Property: The associative property of multiplication states that you can group the numbers differently without affecting the final product: (a x b) x c = a x (b x c). This allows for strategic grouping to simplify the calculation. For instance:
- (4 x 3) x 4 = 12 x 4 = 48
- 4 x (3 x 4) = 4 x 12 = 48
3. Mental Math: With practice, one can perform this calculation mentally. Recognizing that 4 x 3 is 12, and then multiplying 12 by 4, can be done quickly with a little mental agility.
Beyond the Calculation: Exploring the Concepts
While calculating 4 x 3 x 4 is relatively straightforward, the expression offers an opportunity to delve into deeper mathematical concepts:
-
Factors and Multiples: In the expression 4 x 3 x 4, 4 and 3 are factors of 48. 48 is a multiple of 4 and 3. Understanding factors and multiples is crucial for various mathematical operations, including factoring, simplifying fractions, and solving equations.
-
Prime Factorization: Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves). The prime factorization of 48 is 2 x 2 x 2 x 2 x 3 (or 2<sup>4</sup> x 3). This concept is vital in number theory and cryptography.
-
Exponents: The prime factorization highlights the use of exponents. The repeated multiplication of 2 can be expressed concisely as 2<sup>4</sup>, where 4 is the exponent, indicating the number of times 2 is multiplied by itself. Exponents are essential for simplifying complex expressions and solving advanced mathematical problems.
-
Volume Calculation: In the realm of geometry, 4 x 3 x 4 could represent the dimensions of a rectangular prism (length x width x height). The product 48 would then represent the volume of that prism in cubic units. This illustrates a practical application of multiplication in three-dimensional space.
Real-World Applications: Where 4 x 3 x 4 Might Appear
The seemingly simple calculation of 4 x 3 x 4 has widespread real-world applications:
-
Packaging and Shipping: Imagine a box containing four layers of items, with each layer having three rows and four columns. The total number of items would be 4 x 3 x 4 = 48.
-
Inventory Management: A warehouse might stock four pallets of products, each pallet having three stacks, each stack containing four boxes. The total number of boxes would be 4 x 3 x 4 = 48.
-
Construction and Building: Calculating the number of bricks needed for a wall section, the volume of a concrete foundation, or the total number of tiles for a floor could involve similar multiplications.
-
Event Planning: Organizing chairs for an event might involve arranging them in four rows, three columns, and four sections. The total number of chairs would be 4 x 3 x 4 = 48.
-
Data Analysis and Programming: In computer science, multiplication is fundamental for array indexing, loop iterations, and many other processes. Understanding multiplication is essential for programmers and data analysts.
Frequently Asked Questions (FAQ)
Q: Does the order of multiplication matter in 4 x 3 x 4?
A: No, thanks to the commutative and associative properties of multiplication, the order of the numbers doesn't affect the final product. You can multiply them in any order (4 x 3 x 4, 4 x 4 x 3, 3 x 4 x 4, etc.), and you will always get 48.
Q: What if we had a different equation, say 5 x 2 x 7? How would the approach change?
A: The approach would remain the same. You would still perform the multiplications sequentially or use the associative property to group the numbers for easier calculation. The principles remain consistent regardless of the numbers involved.
Q: How can I improve my multiplication skills?
A: Practice is key! Start with smaller numbers and gradually work your way up to larger ones. Use flashcards, online games, and mental math exercises to improve your speed and accuracy. Understanding the times tables is fundamental.
Q: What are some other ways to represent 4 x 3 x 4?
A: You could represent it as 4 x 12, 3 x 16, or as 48 (the product). You could also visually represent it using arrays or diagrams showing four groups of three groups of four items.
Conclusion: The Significance of a Simple Equation
The seemingly simple equation 4 x 3 x 4, while yielding a straightforward answer of 48, serves as a gateway to understanding fundamental mathematical principles and their broad applications in the real world. From the commutative and associative properties to the concepts of factors, multiples, prime factorization, exponents, and volume calculations, this expression reveals the interconnectedness of mathematical ideas. Its practical applications span various fields, highlighting the importance of mastering this basic arithmetic operation. By understanding this equation, we not only solve a simple problem but gain a deeper appreciation for the power and versatility of multiplication in shaping our understanding of the world around us. Mastering fundamental concepts like this forms a strong foundation for tackling more complex mathematical challenges and fosters a deeper appreciation for the elegance and utility of mathematics.
Latest Posts
Latest Posts
-
8 Ounce Water In Ml
Sep 17, 2025
-
How Long Is 25 Metres
Sep 17, 2025
-
120 Km Hr To Mph
Sep 17, 2025
-
Second Longest River On Earth
Sep 17, 2025
-
20 Thousand Pounds In Dollars
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 4 X 3 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.