45 Percent As A Fraction
plugunplug
Sep 19, 2025 · 5 min read
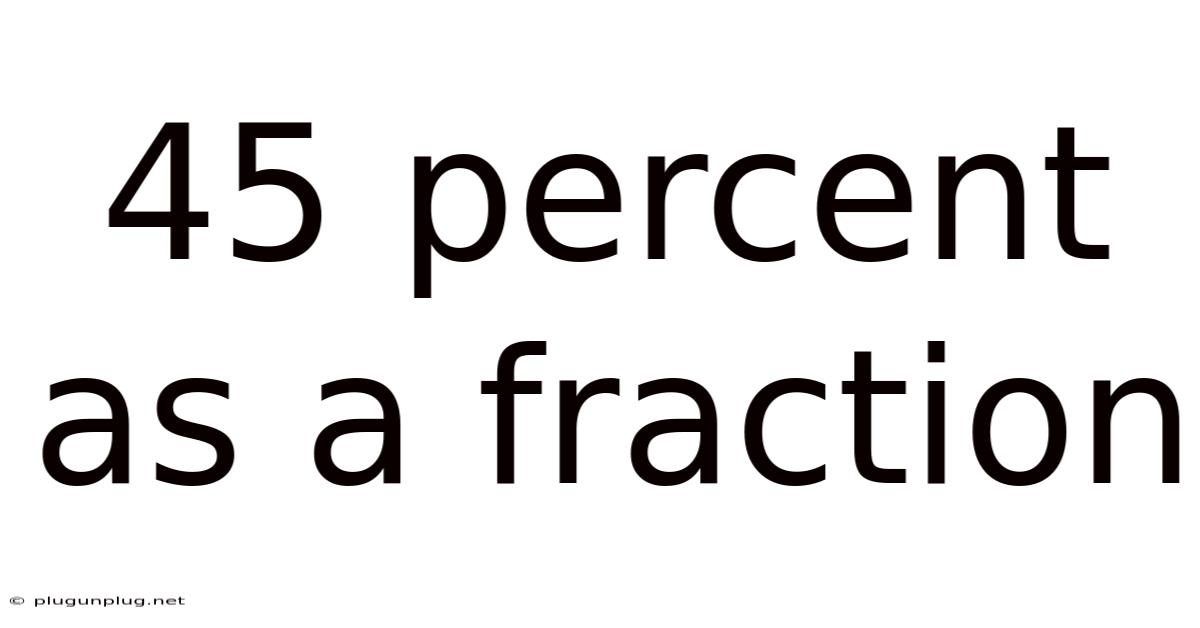
Table of Contents
45 Percent as a Fraction: A Comprehensive Guide
Understanding percentages and their fractional equivalents is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday calculations. This comprehensive guide delves into the intricacies of representing 45 percent as a fraction, exploring different methods, simplifying techniques, and providing a deeper understanding of the underlying concepts. We'll also address common misconceptions and answer frequently asked questions to ensure a thorough grasp of the topic.
Introduction: Understanding Percentages and Fractions
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, 45 percent (45%) means 45 out of 100. Fractions, on the other hand, represent a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). Converting percentages to fractions involves understanding this fundamental relationship. This guide will show you how to convert 45% into its fractional form, simplify it to its lowest terms, and understand the underlying mathematical principles.
Step-by-Step Conversion: 45% to a Fraction
The process of converting a percentage to a fraction is straightforward:
-
Write the percentage as a fraction with a denominator of 100: 45% can be written as 45/100. This directly reflects the definition of percentage – 45 parts out of 100.
-
Simplify the fraction: This step involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD is the largest number that divides both 45 and 100 without leaving a remainder. In this case, the GCD of 45 and 100 is 5.
-
Divide both the numerator and the denominator by the GCD: Dividing 45 by 5 gives 9, and dividing 100 by 5 gives 20.
-
The simplified fraction: Therefore, 45% as a fraction is 9/20. This is the simplest form because 9 and 20 share no common divisors other than 1.
Visual Representation and Real-World Examples
Imagine a pizza cut into 100 equal slices. 45% represents 45 of those slices. If you were to group these slices into sets of 5, you would have 9 groups of 5 slices each, representing 9/20 of the entire pizza. This visual representation helps solidify the understanding of the equivalence between 45%, 45/100, and 9/20.
Different Methods for Conversion
While the method above is the most common and straightforward, there are other approaches to converting 45% to a fraction:
-
Using decimal representation: You can first convert 45% to a decimal by dividing by 100 (45/100 = 0.45). Then, you can convert the decimal to a fraction by writing it over 1 (0.45/1). To eliminate the decimal point, multiply both the numerator and the denominator by 100 (45/100). This leads to the same fraction, 45/100, which simplifies to 9/20.
-
Using proportional reasoning: You can think of it as a proportion: 45/100 = x/y, where x and y are the numerator and denominator of the simplified fraction. Finding equivalent fractions through proportional reasoning leads to the same simplified result of 9/20.
Understanding the Mathematical Principles
The process of simplifying fractions hinges on the concept of greatest common divisor (GCD) or highest common factor (HCF). Finding the GCD allows us to reduce a fraction to its simplest form, which is essential for ease of understanding and comparison. There are various methods for finding the GCD, including:
-
Listing factors: List all the factors of both the numerator and the denominator, and identify the largest common factor.
-
Prime factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power. For example, 45 = 3² x 5 and 100 = 2² x 5². The only common prime factor is 5 (raised to the power of 1), making the GCD 5.
-
Euclidean algorithm: This is an efficient algorithm for finding the GCD, particularly useful for larger numbers.
Frequently Asked Questions (FAQ)
-
Can 45% be expressed as a mixed number? No, because the numerator (9) is smaller than the denominator (20), it remains a proper fraction. A mixed number is only used when the numerator is greater than or equal to the denominator.
-
What are some other examples of percentage to fraction conversions? Let's look at a few: 25% = 1/4, 50% = 1/2, 75% = 3/4, 10% = 1/10, 20% = 1/5. Notice a pattern? Many common percentages have easily recognizable fractional equivalents.
-
Why is simplifying fractions important? Simplifying fractions makes them easier to understand, compare, and use in further calculations. A simplified fraction represents the same value as the original fraction but in a more concise form.
Conclusion: Mastering Percentage to Fraction Conversions
Converting 45% to its fractional equivalent of 9/20 is a fundamental mathematical skill with far-reaching applications. This guide has provided a comprehensive explanation, covering various methods, underlying mathematical principles, and practical examples. By understanding the concept of percentages, fractions, and the process of simplification, you can confidently tackle similar conversions and apply this knowledge in various real-world scenarios. Remember, the ability to work comfortably with percentages and fractions is an essential tool for success in many academic and professional pursuits. Practice makes perfect, so continue practicing these conversions to build your fluency and understanding. This will allow you to move beyond simply finding the answer and truly grasping the underlying mathematical concepts and their applications.
Latest Posts
Latest Posts
-
Constantinople Where Is It Located
Sep 19, 2025
-
Who Were The Big Three
Sep 19, 2025
-
Definition Of A Concrete Poem
Sep 19, 2025
-
What Was Agreed At Yalta
Sep 19, 2025
-
30 Celsius To Fahrenheit Conversion
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 45 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.