5 9 Divided By 5
plugunplug
Sep 24, 2025 · 5 min read
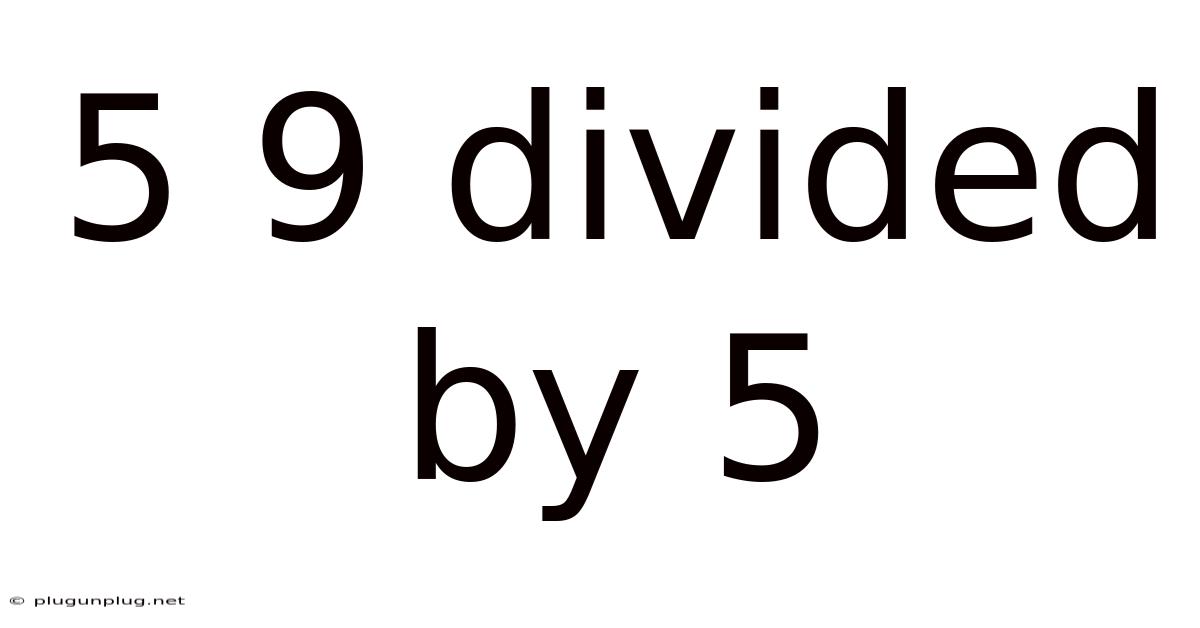
Table of Contents
Decoding 59 Divided by 5: A Deep Dive into Division and Remainders
This article explores the seemingly simple calculation of 59 divided by 5, delving far beyond the basic answer to uncover the underlying mathematical principles, practical applications, and broader implications of division with remainders. We'll journey from elementary arithmetic to more advanced concepts, ensuring a comprehensive understanding for readers of all levels. This will cover various methods of calculation, explore the meaning of the quotient and remainder, and demonstrate the importance of this fundamental operation in various fields. Understanding division, especially with remainders, is crucial for grasping more complex mathematical concepts and problem-solving in everyday life.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the inverse operation of multiplication; it answers the question: "How many times does one number (the divisor) go into another number (the dividend)?" In the case of 59 divided by 5, 5 is the divisor, and 59 is the dividend.
The result of division is typically expressed as a quotient and, in many cases, a remainder. The quotient represents the number of times the divisor fits completely into the dividend, while the remainder represents the amount left over after the division is complete.
Example: If you have 12 apples and want to divide them equally among 4 friends, you perform the division 12 ÷ 4 = 3. Here, 3 is the quotient, representing the number of apples each friend receives. There is no remainder because 4 divides evenly into 12.
Calculating 59 Divided by 5: Different Approaches
Let's tackle the core problem: 59 ÷ 5. We can approach this using several methods:
1. Long Division: This is a classic method taught in elementary school.
11
5 | 59
-5
09
-5
4
This shows that 5 goes into 59 eleven times (the quotient) with a remainder of 4. This means that 59 can be expressed as 5 x 11 + 4.
2. Repeated Subtraction: We can repeatedly subtract the divisor (5) from the dividend (59) until we reach a number less than the divisor.
59 - 5 = 54 54 - 5 = 49 49 - 5 = 44 44 - 5 = 39 39 - 5 = 34 34 - 5 = 29 29 - 5 = 24 24 - 5 = 19 19 - 5 = 14 14 - 5 = 9 9 - 5 = 4
We subtracted 5 eleven times before reaching a remainder of 4.
3. Using Fractions: Division can be represented as a fraction. 59 ÷ 5 can be written as 59/5. This fraction can be converted to a mixed number:
59/5 = 11 4/5
The whole number part (11) is the quotient, and the fraction (4/5) represents the remainder as a fraction of the divisor.
The Significance of the Quotient and Remainder
The quotient and remainder provide valuable information about the division process. In the case of 59 ÷ 5 = 11 R 4:
-
Quotient (11): This represents the whole number of times 5 fits into 59. It provides an approximation if we need a whole number answer. For example, if we're dividing 59 candies equally among 5 children, each child gets 11 candies.
-
Remainder (4): This represents the portion of the dividend that's left over after the equal distribution. In our candy example, there are 4 candies remaining. This remainder is crucial because it represents the part that wasn't fully divisible.
Real-World Applications of Division with Remainders
Division with remainders isn't just an abstract mathematical concept; it has numerous practical applications in everyday life and various professions:
-
Equal Sharing: Dividing resources equally among a group of people.
-
Measurement: Converting units of measurement (e.g., converting inches to feet).
-
Scheduling: Determining the number of shifts needed for a certain number of hours of work.
-
Inventory Management: Calculating the number of full boxes needed to pack a certain quantity of items.
-
Computer Science: Remainders are critical in various algorithms and processes, including hashing and modular arithmetic (used in cryptography).
-
Engineering: Calculating the number of parts needed for a project, considering possible waste or leftover materials.
Beyond the Basics: Exploring Modular Arithmetic
The remainder in a division problem has special significance in modular arithmetic. Modular arithmetic is a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value—the modulus. In the case of 59 ÷ 5, the modulus is 5, and the remainder (4) is the result in modulo 5 arithmetic (written as 59 ≡ 4 (mod 5)). This concept is fundamental in number theory, cryptography, and computer science.
Frequently Asked Questions (FAQ)
Q: Can the remainder ever be larger than the divisor?
A: No. By definition, the remainder must be smaller than the divisor. If the remainder is larger than or equal to the divisor, it means the division process isn't complete, and the quotient needs to be increased.
Q: What happens if the dividend is smaller than the divisor?
A: If the dividend is smaller than the divisor, the quotient is 0, and the remainder is equal to the dividend. For example, 4 ÷ 5 = 0 R 4.
Q: Are there other ways to express the result of 59 ÷ 5?
A: Yes. Besides the quotient and remainder (11 R 4), we can express the result as a decimal (11.8), a mixed number (11 4/5), or using modular arithmetic (59 ≡ 4 (mod 5)). The best representation depends on the context of the problem.
Q: Why is understanding remainders important?
A: Remainders provide crucial information about the completeness of the division and are essential in various applications, especially in scenarios where equal sharing or precise measurement is required. Ignoring the remainder can lead to inaccurate results or incomplete solutions.
Conclusion: The Enduring Importance of Division
The seemingly simple calculation of 59 divided by 5 opens a door to a world of mathematical concepts and practical applications. Understanding the process, the meaning of the quotient and remainder, and the implications of division with remainders is crucial for problem-solving in various fields. From everyday tasks like sharing resources to complex algorithms in computer science, mastering this fundamental operation equips us with essential tools for navigating a quantitative world. Remember, the beauty of mathematics often lies in the intricate details and connections hidden within seemingly simple problems. The next time you encounter a division problem, take a moment to appreciate the depth and breadth of its implications.
Latest Posts
Latest Posts
-
How Do You Spell Cat
Sep 24, 2025
-
Use Assent In A Sentence
Sep 24, 2025
-
What Is Lcm In Mathematics
Sep 24, 2025
-
Units Of Computer Transmission Speed
Sep 24, 2025
-
0 15 Recurring As A Fraction
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 5 9 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.