5 Divided By 5 3
plugunplug
Sep 18, 2025 · 5 min read
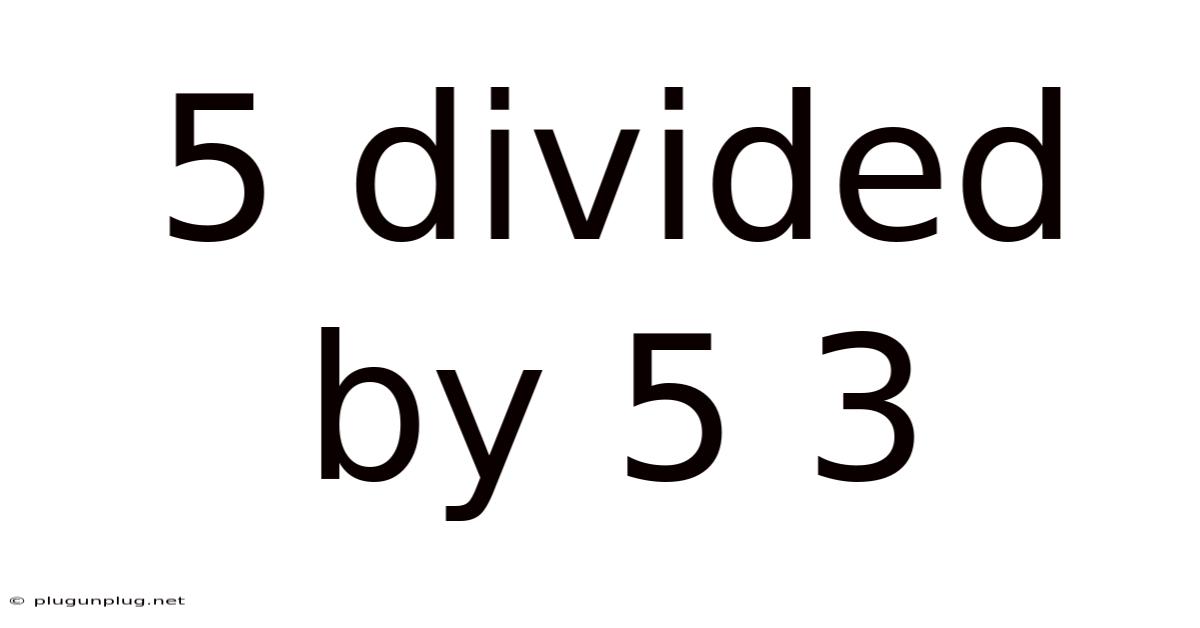
Table of Contents
Decoding 5 Divided by 5/3: A Deep Dive into Fraction Division
This article explores the seemingly simple yet conceptually rich problem of 5 divided by 5/3. We'll dissect this calculation step-by-step, providing a clear understanding of the underlying principles of fraction division, and exploring different approaches to solving it. Understanding this seemingly basic operation is crucial for building a strong foundation in mathematics and for tackling more complex problems involving fractions and ratios. We'll delve into the mathematical reasoning, address common misconceptions, and offer practical examples to solidify your understanding.
Understanding Fraction Division: The "Invert and Multiply" Rule
Before tackling 5 divided by 5/3, let's refresh our understanding of dividing by fractions. The core concept is that dividing by a fraction is the same as multiplying by its reciprocal (or inverse). The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
This "invert and multiply" rule is a fundamental principle in mathematics, and its application makes fraction division much simpler. Instead of grappling with the abstract concept of dividing by a fraction, we transform the problem into a familiar multiplication problem. This approach significantly streamlines the calculation and reduces the risk of errors.
Step-by-Step Solution: 5 Divided by 5/3
Now, let's apply this principle to solve 5 divided by 5/3:
-
Rewrite the problem: We can rewrite the problem as a fraction: 5 ÷ (5/3).
-
Find the reciprocal: The reciprocal of 5/3 is 3/5.
-
Convert to multiplication: The division problem now becomes a multiplication problem: 5 x (3/5).
-
Simplify and solve: We can simplify this expression. Notice that we have a 5 in the numerator and a 5 in the denominator. These cancel each other out (5/5 = 1). This leaves us with: 1 x 3 = 3.
Therefore, 5 divided by 5/3 equals 3.
Visualizing the Problem: A Practical Approach
While the "invert and multiply" rule provides a clear and efficient method for solving the problem, a visual approach can enhance understanding, especially for those who benefit from concrete examples.
Imagine you have 5 pizzas. You want to divide these pizzas into servings of 5/3 of a pizza each. How many servings can you make?
To visualize this, consider that 5/3 of a pizza is equivalent to one pizza and 2/3 of another pizza. If you divide your 5 pizzas into servings of 1 and 2/3 pizzas, you will obtain exactly 3 servings. This visual representation confirms our calculated answer.
Mathematical Explanation: Connecting to the Concept of Ratios
The problem 5 ÷ (5/3) can be interpreted as asking: "How many times does 5/3 fit into 5?"
This question directly relates to the concept of ratios. We are essentially comparing the ratio of 5 to 5/3. We can solve this by setting up a proportion:
5 / x = 5/3 / 1
Cross-multiplying gives us:
5 * 1 = x * (5/3)
5 = (5x)/3
Multiplying both sides by 3 gives us:
15 = 5x
Dividing both sides by 5 gives us:
x = 3
Again, this confirms that 5 divided by 5/3 equals 3.
Addressing Common Misconceptions
A common mistake when dividing fractions is forgetting to invert the second fraction before multiplying. Remember, we are not simply multiplying the numerators and denominators directly. Always invert the divisor (the fraction you are dividing by) before proceeding with the multiplication.
Another misconception involves incorrectly simplifying before inverting. The order of operations is crucial. You must first identify the division operation, invert the divisor, and then proceed with simplification and multiplication.
Extending the Concept: Dividing by Other Fractions
The principles discussed here apply to any division problem involving fractions. For instance, let's consider 7 divided by 2/5:
-
Rewrite as a fraction: 7 ÷ (2/5)
-
Find the reciprocal of 2/5: 5/2
-
Convert to multiplication: 7 x (5/2)
-
Solve: (7 x 5) / 2 = 35/2 = 17.5
Therefore, 7 divided by 2/5 equals 17.5.
Real-World Applications: Fractions in Everyday Life
Understanding fraction division is not merely an academic exercise. It has practical applications in numerous everyday situations:
-
Cooking and Baking: Recipes often involve fractional measurements, and accurately dividing ingredients requires a grasp of fraction division.
-
Sewing and Crafts: Calculating fabric requirements or dividing materials for projects frequently involves fractions.
-
Construction and Engineering: Precise measurements and calculations in construction rely heavily on fraction arithmetic.
-
Finance and Budgeting: Managing finances often necessitates working with fractions and percentages, which necessitates understanding fraction division.
Frequently Asked Questions (FAQs)
-
Q: Why do we invert and multiply when dividing fractions?
- A: Dividing by a fraction is equivalent to multiplying by its reciprocal. This transformation simplifies the calculation and aligns with the fundamental properties of arithmetic.
-
Q: What if the whole number is a fraction itself?
- A: The same principle applies. For instance, (3/4) ÷ (2/5) would be solved by inverting 2/5 to 5/2 and multiplying: (3/4) x (5/2) = 15/8.
-
Q: Can I use a calculator to solve these problems?
- A: Yes, most calculators can handle fraction division directly. However, understanding the underlying principles is crucial for developing mathematical proficiency.
-
Q: Are there alternative methods to solve fraction division problems?
- A: While the "invert and multiply" method is the most efficient and commonly used, other methods exist, such as converting fractions to decimals before performing the division. However, these methods can be less efficient and introduce the possibility of rounding errors.
Conclusion: Mastering Fraction Division
Mastering fraction division is a key step in developing a strong foundation in mathematics. By understanding the "invert and multiply" rule, visualizing the problem, and practicing with various examples, you can confidently tackle even the most complex fraction division problems. The ability to handle fractions efficiently is invaluable, both in academic settings and in numerous real-world applications. Remember to always focus on understanding the underlying principles; this will make solving these problems not only easier but also more rewarding. The journey to mathematical fluency is built on understanding these foundational concepts and practicing their application.
Latest Posts
Latest Posts
-
Digoxin Toxicity Signs And Symptoms
Sep 18, 2025
-
6 Foot 1 In Metres
Sep 18, 2025
-
Past Tense Of To Lead
Sep 18, 2025
-
Another Name For Mitral Valve
Sep 18, 2025
-
Meaning Of Community In Biology
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 5 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.