5 X 3 X 1
plugunplug
Sep 17, 2025 · 7 min read
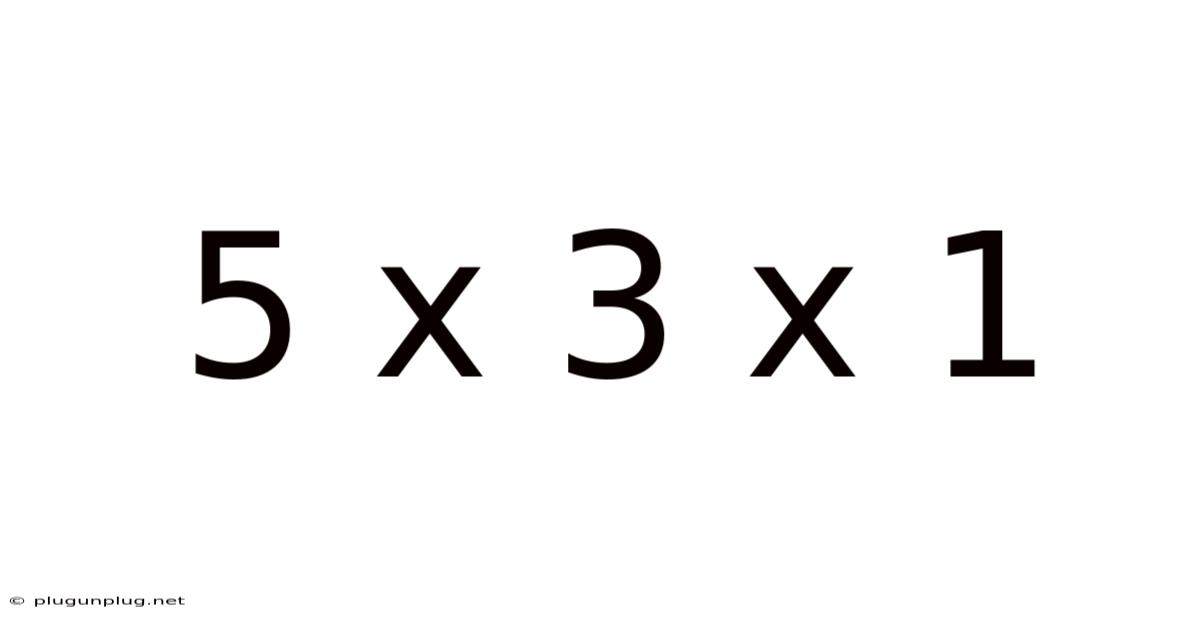
Table of Contents
Decoding 5 x 3 x 1: Exploring Dimensions, Applications, and Interpretations
This article delves into the seemingly simple expression "5 x 3 x 1," exploring its various interpretations across different fields, from basic arithmetic to more complex applications in geometry, physics, and even abstract thought. While the numerical result is straightforward (15), the underlying concepts and potential applications are far richer and more intriguing than a simple multiplication problem might suggest. We will unpack this expression, examining its fundamental meaning and exploring its surprising relevance in diverse contexts.
I. The Fundamental Arithmetic Interpretation: 5 x 3 x 1 = 15
At its most basic level, "5 x 3 x 1" represents a multiplication problem. It signifies that we are multiplying the numbers 5, 3, and 1 together. The order of multiplication does not affect the outcome due to the commutative property of multiplication. Therefore, 5 x 3 x 1 = 15, 5 x 1 x 3 = 15, 3 x 5 x 1 = 15, and so on. This simple calculation forms the foundation for understanding the more complex interpretations that follow. It emphasizes the fundamental concept of repeated addition or scaling. Multiplying by 1 implies no change, highlighting the multiplicative identity. Multiplying by 3 represents a threefold increase, and multiplying by 5 represents a fivefold increase. The final product, 15, represents the cumulative effect of these scaling operations.
II. Geometric Interpretations: Volume and Dimensions
The expression "5 x 3 x 1" can be interpreted geometrically as the dimensions of a rectangular prism (or cuboid). Imagine a box with:
- Length: 5 units
- Width: 3 units
- Height: 1 unit
The result of 5 x 3 x 1 (15) represents the volume of this box, expressed in cubic units. This interpretation bridges the gap between abstract mathematical concepts and tangible, real-world objects. This simple example can be extended to understand volume calculations in various contexts, from packaging design to architectural planning. Consider the practical implications: A box with these dimensions might hold 15 liters of liquid, 15 cubic feet of sand, or 15 units of any other measurable quantity. The simplicity of the numerical calculation belies the practical utility of understanding spatial relationships and volume calculations.
III. Applications in Physics and Engineering: Vectors and Scalar Quantities
In physics, the numbers could represent vector components or scalar quantities. For example:
-
Velocity: Imagine an object moving with a velocity vector. The three numbers could represent components along three orthogonal axes (x, y, z). However, in this context, the multiplication doesn't directly translate into a simple product. Vector operations are more complex and involve dot products or cross products, depending on the physical context. Understanding this context highlights that simple multiplication is only part of the broader physics toolbox.
-
Force: Three forces of magnitudes 5, 3, and 1 units might be acting on an object. Here, the individual forces need to be analyzed using vector addition and resolution to determine the net force on the object, depending on their direction. Again, 5 x 3 x 1 = 15 is not a direct representation of the net force.
-
Scalar Quantities: In contrast to vectors, scalar quantities only possess magnitude. Imagine 5 kg of material, 3 meters of length, and a single item (1). While multiplication might make sense in some contexts (e.g., calculating the total mass of 5 identical 3-meter-long rods, each weighing 1 kg), it's critical to understand that the product has a specific physical meaning within its context.
This application emphasizes the importance of context and the limitations of applying simple mathematical operations blindly to physical phenomena.
IV. Combinatorial Interpretations: Permutations and Arrangements
The expression can also be approached from a combinatorial perspective. Imagine you have:
- 5 choices for Option A
- 3 choices for Option B
- 1 choice for Option C
The number of different combinations of A, B, and C you can create is 5 x 3 x 1 = 15. This is a fundamental counting principle, demonstrating the calculation of the size of the sample space. This approach has significant applications in probability and statistics, where the number of possible outcomes is a crucial element in determining the likelihood of specific events. The simplicity of the multiplication hides the power of combinatorics in determining the total number of possible arrangements or combinations.
V. Abstract and Philosophical Interpretations: Multiplicative Relationships
Stepping beyond concrete applications, we can examine "5 x 3 x 1" as a representation of multiplicative relationships. The numbers could symbolize abstract qualities or quantities:
- Scale: The number 5 represents a scaling factor, amplifying the effects of the other numbers.
- Intensity: The number 3 signifies an intensity or magnitude, contributing to the overall outcome.
- Constraint: The number 1 acts as a constraint, representing a fixed or unchanging factor.
This interpretation emphasizes the importance of relative scales and intensities in various systems. The relationships between these factors could model aspects of complex phenomena in social sciences, ecology, or other fields where interacting factors combine to create an overall outcome. Interpreting the numbers symbolically allows us to analyze the relative contributions of different factors to a system's overall behavior.
VI. Expanding the Concept: Beyond Three Dimensions
While the initial example uses three numbers, the principle of multiplication can be extended to any number of dimensions. For example, 5 x 3 x 1 x 2 would represent the volume of a hyper-rectangular prism in four dimensions, a concept frequently encountered in advanced mathematics and physics. The application of this concept allows for the exploration of higher-dimensional spaces and their properties, highlighting the scalability and versatility of the mathematical tools we employ. The concept easily extends to higher dimensions, showcasing the foundational nature of simple multiplication in more complex mathematical structures.
VII. Mathematical Properties and Implications
The expression "5 x 3 x 1" showcases several important mathematical properties:
-
Commutative Property: The order of multiplication doesn't matter; the result remains the same. This is a fundamental property of multiplication that simplifies calculations.
-
Associative Property: The grouping of numbers doesn't affect the result. (5 x 3) x 1 = 5 x (3 x 1) = 15. This property allows for flexibility in performing calculations.
-
Multiplicative Identity: Multiplying any number by 1 results in the same number. This property is crucial in various mathematical manipulations.
Understanding these fundamental properties strengthens the ability to perform calculations efficiently and correctly. It also demonstrates the inherent structure and logic underpinning seemingly straightforward arithmetic operations.
VIII. Frequently Asked Questions (FAQ)
Q: What are some real-world examples where 5 x 3 x 1 is used?
A: Numerous examples exist, including calculating the volume of a box, determining the number of combinations in a simple decision-making process, or representing simple multiplicative relationships in various systems. Specific applications depend heavily on the context and the meaning assigned to the numbers.
Q: Can the numbers represent anything other than physical quantities?
A: Absolutely. The numbers can represent abstract concepts, relative scales, intensities, or constraints within a particular model or system. The meaning is entirely dependent on the context in which they are used.
Q: How does this relate to more advanced mathematics?
A: The fundamental concepts of multiplication and the properties discussed extend to more advanced mathematical fields, such as linear algebra, calculus, and abstract algebra. The simplicity of 5 x 3 x 1 provides a foundation upon which more complex mathematical constructs are built.
IX. Conclusion: The Depth of Simplicity
While seemingly trivial, the expression "5 x 3 x 1" unveils a surprising depth of meaning and application across diverse fields. From basic arithmetic to complex geometric interpretations, physical models, combinatorial analysis, and even abstract representations, this simple equation reveals the power of mathematical concepts and their ability to model and understand a vast array of phenomena. The seemingly straightforward calculation underscores the importance of understanding the context and the underlying principles to correctly interpret and apply mathematical tools effectively. Its simplicity belies its power and its relevance to a surprisingly wide range of disciplines, reinforcing the fundamental role of mathematics in our understanding of the world.
Latest Posts
Latest Posts
-
8 Ounce Water In Ml
Sep 17, 2025
-
How Long Is 25 Metres
Sep 17, 2025
-
120 Km Hr To Mph
Sep 17, 2025
-
Second Longest River On Earth
Sep 17, 2025
-
20 Thousand Pounds In Dollars
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 5 X 3 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.