5 X 4 X 3
plugunplug
Sep 23, 2025 · 6 min read
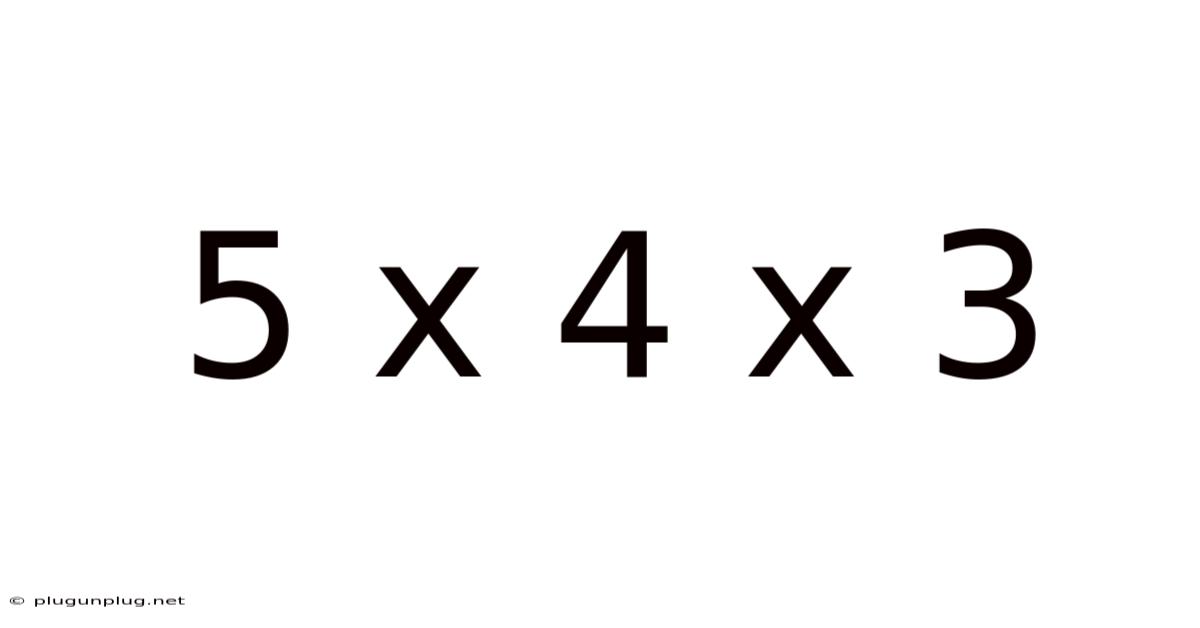
Table of Contents
Unveiling the Mysteries of 5 x 4 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 5 x 4 x 3, delving far beyond the basic answer to uncover the underlying mathematical principles and its diverse applications in various fields. We'll examine the concept of multiplication itself, explore different methods for solving this problem, and discuss how this seemingly simple equation plays a significant role in more complex mathematical concepts and real-world scenarios. Understanding 5 x 4 x 3 provides a stepping stone to comprehending more advanced mathematical concepts and problem-solving strategies.
Understanding Multiplication: The Building Block of Arithmetic
Before we tackle 5 x 4 x 3, let's revisit the fundamental concept of multiplication. Multiplication is essentially repeated addition. For example, 5 x 4 means adding five four times: 4 + 4 + 4 + 4 + 4 = 20. This fundamental understanding is crucial for grasping the essence of multiplication and its extensions into more complex calculations. It's the foundation upon which we build our understanding of more advanced mathematical operations.
Solving 5 x 4 x 3: Multiple Approaches
There are several ways to solve 5 x 4 x 3, each illustrating different properties of multiplication:
1. Sequential Multiplication: This is the most straightforward approach. We perform the multiplication step-by-step:
- First, multiply 5 by 4: 5 x 4 = 20
- Then, multiply the result by 3: 20 x 3 = 60
Therefore, 5 x 4 x 3 = 60.
2. Commutative Property: The commutative property of multiplication states that the order of the numbers doesn't affect the result. This means we can rearrange the numbers and still get the same answer. We can use this to our advantage:
- Multiply 4 and 3 first: 4 x 3 = 12
- Then multiply the result by 5: 12 x 5 = 60
This demonstrates the flexibility of multiplication and highlights a key property that simplifies calculations.
3. Associative Property: The associative property allows us to group the numbers differently. We can group (5 x 4) x 3 or 5 x (4 x 3) and still arrive at the same answer. This property is particularly useful when dealing with larger numbers or more complex equations. Both grouping methods lead to the same result: 60.
4. Using Visual Aids: Visual aids, such as arrays or diagrams, can be particularly helpful, especially for visualizing multiplication and understanding the concept of repeated addition. Imagine a rectangular array with 5 rows and 4 columns. Each cell represents one unit. The total number of cells would be 5 x 4 = 20. If we then stack 3 of these arrays on top of each other, we have 3 x 20 = 60 units. This visual approach reinforces the concept of multiplication.
Expanding the Concept: Beyond the Basic Calculation
While 5 x 4 x 3 = 60 is a simple calculation, understanding the underlying principles allows us to apply it to more complex scenarios:
-
Volume Calculation: Imagine a rectangular box with dimensions of 5 units, 4 units, and 3 units. The volume of this box is calculated by multiplying these dimensions: 5 x 4 x 3 = 60 cubic units. This demonstrates the practical application of multiplication in geometry.
-
Combinatorics: If you have 5 shirts, 4 pants, and 3 pairs of shoes, the total number of different outfits you can create is 5 x 4 x 3 = 60. This illustrates how multiplication is used in combinatorics to calculate the number of possible arrangements or combinations.
-
Probability: Multiplication is also fundamental in probability calculations. If the probability of three independent events occurring is 5/10, 4/10, and 3/10 respectively, the probability of all three events happening is (5/10) x (4/10) x (3/10) = 60/1000 = 6/100 or 3/50.
-
Factorials: Factorials (!), which represent the product of all positive integers up to a given number, are directly related to multiplication. For example, 5! (5 factorial) is 5 x 4 x 3 x 2 x 1 = 120. This is a crucial concept in probability and combinatorics. Understanding the 5 x 4 x 3 component within this larger calculation is essential.
-
Algebraic Expressions: The principles illustrated by 5 x 4 x 3 are applicable to algebraic expressions. Consider an expression like 5x * 4y * 3z. The numerical part can be calculated as 5 x 4 x 3 = 60, leaving the expression as 60xyz. This showcases the fundamental nature of multiplication within algebraic manipulation.
The Significance of Order of Operations (PEMDAS/BODMAS)
While the commutative and associative properties allow us to rearrange the numbers in 5 x 4 x 3, the order of operations becomes crucial when dealing with more complex expressions involving multiple arithmetic operations. Remember PEMDAS/BODMAS:
- Parentheses/ Brackets
- Exponents/ Orders
- Multiplication and Division (from left to right)
- Addition and Subtraction (from left to right)
This order ensures consistency and accuracy in calculating expressions with multiple operations.
Practical Applications Across Disciplines
The simple calculation of 5 x 4 x 3 has far-reaching implications in diverse fields:
-
Engineering: Calculating volumes, areas, and stresses in structural designs frequently involves multiplication.
-
Computer Science: Multiplication is a fundamental operation in computer programming and algorithm design. Many calculations in graphics, simulations, and data processing rely on multiplication.
-
Finance: Calculating compound interest, profits, and losses involves repeated multiplication.
-
Physics: Numerous physics formulas involve multiplication, from calculating velocities and forces to determining energy levels.
-
Chemistry: Stoichiometry, the study of quantitative relationships in chemical reactions, relies heavily on multiplication.
-
Economics: Economic models and forecasting often utilize multiplicative relationships to model growth, inflation, and other economic factors.
Frequently Asked Questions (FAQ)
Q: Why is the order of multiplication not important in this specific case?
A: Because multiplication is both commutative and associative, the order in which we multiply 5, 4, and 3 does not change the final result. This is a unique property of multiplication.
Q: What if there were more numbers involved?
A: The same principles apply. You would continue to multiply the numbers sequentially, using the commutative and associative properties for efficiency, and remembering the order of operations if other arithmetic operations are involved.
Q: How does this relate to division?
A: Multiplication and division are inverse operations. If 5 x 4 x 3 = 60, then 60 / 3 = 20, 20 / 4 = 5, and 5 / 5 = 1. Understanding this relationship is key to solving a wider range of mathematical problems.
Conclusion: A Foundation for Future Learning
The seemingly simple equation, 5 x 4 x 3 = 60, serves as a powerful illustration of fundamental mathematical concepts. Understanding this calculation, and the underlying principles of multiplication, provides a solid base for tackling more advanced mathematical problems and real-world applications across a wide spectrum of disciplines. By grasping the essence of multiplication and its properties, we build a strong foundation for future learning and problem-solving endeavors. This simple equation unlocks doors to more complex mathematical concepts, reinforcing the importance of mastering fundamental principles in mathematics. From calculating volumes and areas to navigating complex probability calculations and intricate algebraic expressions, the principles learned from solving 5 x 4 x 3 are invaluable tools for navigating the world of mathematics and its applications.
Latest Posts
Latest Posts
-
John Dalton Name Of Model
Sep 23, 2025
-
Causes Of The 1917 Revolution
Sep 23, 2025
-
Is Nitrogen A Diatomic Molecule
Sep 23, 2025
-
120 Km H In Mph
Sep 23, 2025
-
What Is 49kg In Stones
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 X 4 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.