9 Divided By 1 2
plugunplug
Sep 18, 2025 · 6 min read
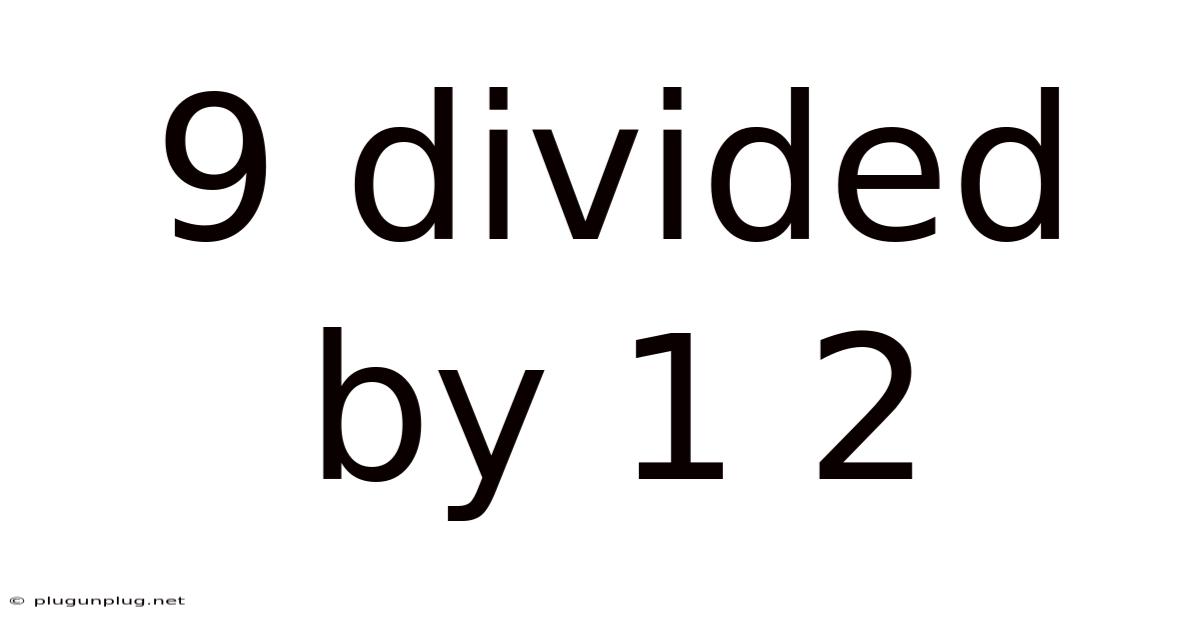
Table of Contents
9 Divided by 1/2: Unraveling the Math Behind a Seemingly Simple Problem
Many people struggle with fraction division, even seemingly straightforward problems like 9 divided by 1/2. This article will delve into the intricacies of this calculation, providing a step-by-step guide, exploring the underlying mathematical principles, and addressing common misconceptions. Understanding this concept is crucial for mastering fractions and building a solid foundation in mathematics. We will uncover the answer and, more importantly, why that answer is correct.
Understanding Fraction Division: The "Keep, Change, Flip" Method
Before tackling 9 divided by 1/2 (written as 9 ÷ 1/2), let's refresh our understanding of dividing by fractions. The most common and intuitive method is the "keep, change, flip" method, also known as the reciprocal method. This method simplifies the process by transforming the division problem into a multiplication problem.
Here's the breakdown:
- Keep: Keep the first number (the dividend) as it is. In our case, this is 9.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – find its reciprocal. The reciprocal of a fraction is obtained by swapping the numerator and the denominator. The reciprocal of 1/2 is 2/1, or simply 2.
Therefore, 9 ÷ 1/2 becomes 9 × 2.
Solving the Problem: Step-by-Step
Now, let's apply the "keep, change, flip" method to solve 9 ÷ 1/2:
- Keep: 9
- Change: ÷ becomes ×
- Flip: 1/2 becomes 2/1 (or 2)
So the equation becomes: 9 × 2 = 18
Therefore, 9 divided by 1/2 equals 18.
Visualizing the Solution: A Real-World Analogy
Let's illustrate this with a real-world example to make the concept more concrete. Imagine you have 9 pizzas, and you want to divide them into servings of 1/2 a pizza each. How many servings will you have?
You can visually represent this by cutting each of the 9 pizzas in half. Each pizza will yield 2 servings (1/2 + 1/2 = 1). Since you have 9 pizzas, you'll have a total of 9 × 2 = 18 servings. This visual representation directly corresponds to the mathematical solution.
The Mathematical Explanation: Why Does "Keep, Change, Flip" Work?
The "keep, change, flip" method is not just a trick; it's rooted in the fundamental principles of mathematics. Let's delve into the theoretical underpinnings:
Dividing by a fraction is the same as multiplying by its reciprocal. This can be understood through the concept of multiplicative inverses. Two numbers are multiplicative inverses (or reciprocals) if their product is 1. For example, 1/2 and 2 are multiplicative inverses because (1/2) × 2 = 1.
Consider the general case of dividing a fraction a/b by another fraction c/d:
(a/b) ÷ (c/d)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
(a/b) × (d/c) = (a × d) / (b × c)
In our case, a/b = 9/1 (since 9 can be represented as a fraction) and c/d = 1/2. Applying the formula:
(9/1) ÷ (1/2) = (9/1) × (2/1) = (9 × 2) / (1 × 1) = 18/1 = 18
This demonstrates that the "keep, change, flip" method is not a shortcut but a direct application of the fundamental rules of fraction division.
Common Misconceptions and How to Avoid Them
Several common misconceptions can lead to incorrect answers when dividing by fractions. Let's address some of them:
-
Dividing by a fraction makes the number smaller: This is a prevalent misunderstanding. Dividing by a fraction greater than 1 will result in a smaller number. However, dividing by a fraction less than 1 (like 1/2) actually results in a larger number. This is because dividing by a number less than 1 is equivalent to multiplying by a number greater than 1.
-
Incorrectly applying the "keep, change, flip" method: Ensure you are correctly identifying the dividend and the divisor. The "keep" refers to the number before the division sign. The "flip" applies only to the number after the division sign.
-
Forgetting to convert whole numbers to fractions: Remember, whole numbers can be expressed as fractions with a denominator of 1 (e.g., 9 = 9/1). This conversion is necessary before applying the "keep, change, flip" method.
-
Arithmetic errors: Even with the correct method, careless mistakes in multiplication can lead to errors. Always double-check your calculations.
Expanding the Understanding: Different Approaches
While the "keep, change, flip" method is widely used and efficient, there are other ways to approach fraction division. Understanding these alternative methods can deepen your mathematical intuition:
-
Using the concept of reciprocal: Instead of mechanically applying "keep, change, flip," consciously think about finding the reciprocal of the divisor and then multiplying. This reinforces the underlying mathematical principles.
-
Visual representations: Using diagrams, models, or real-world scenarios can be helpful, especially for beginners. Visualizing the problem can enhance understanding and provide a different perspective.
-
Converting fractions to decimals: While not always practical, converting the fractions to decimals before dividing can sometimes simplify the calculation, particularly if you are more comfortable with decimal arithmetic. However, remember that this may lead to rounding errors in some cases.
Frequently Asked Questions (FAQ)
-
Q: What if I have a mixed number (a whole number and a fraction) instead of just a whole number?
A: First, convert the mixed number into an improper fraction (a fraction where the numerator is larger than the denominator). Then, apply the "keep, change, flip" method. For example, if the problem is 2 ½ ÷ 1/2, convert 2 ½ to 5/2, then proceed with (5/2) ÷ (1/2) = (5/2) × (2/1) = 5.
-
Q: Can I divide a fraction by a whole number using the "keep, change, flip" method?
A: Absolutely! Just remember to express the whole number as a fraction with a denominator of 1. For example, 1/3 ÷ 4 is the same as (1/3) ÷ (4/1) = (1/3) × (1/4) = 1/12.
-
Q: Why is dividing by a fraction the same as multiplying by its reciprocal?
A: This stems from the definition of division as the inverse operation of multiplication. Dividing by a number is equivalent to multiplying by its multiplicative inverse (reciprocal).
Conclusion: Mastering Fraction Division
Mastering fraction division is a cornerstone of mathematical proficiency. The problem of 9 divided by 1/2, while seemingly simple, serves as an excellent example to solidify understanding of the "keep, change, flip" method and the underlying mathematical principles. By understanding the why behind the how, you'll be better equipped to tackle more complex fraction problems with confidence and precision. Remember to practice regularly, use visual aids when necessary, and don't hesitate to explore different approaches to strengthen your grasp of this essential mathematical concept. The seemingly daunting world of fraction division will become much clearer and even enjoyable once you've grasped these fundamental principles.
Latest Posts
Latest Posts
-
200km To Miles Per Hour
Sep 18, 2025
-
What Is Europes Tallest Mountain
Sep 18, 2025
-
What The Capital Of Florida
Sep 18, 2025
-
Is Snape Harry Potters Dad
Sep 18, 2025
-
Is Data Protection Compliance Straightforward
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 9 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.