Hcf Of 18 And 6
plugunplug
Sep 18, 2025 · 7 min read
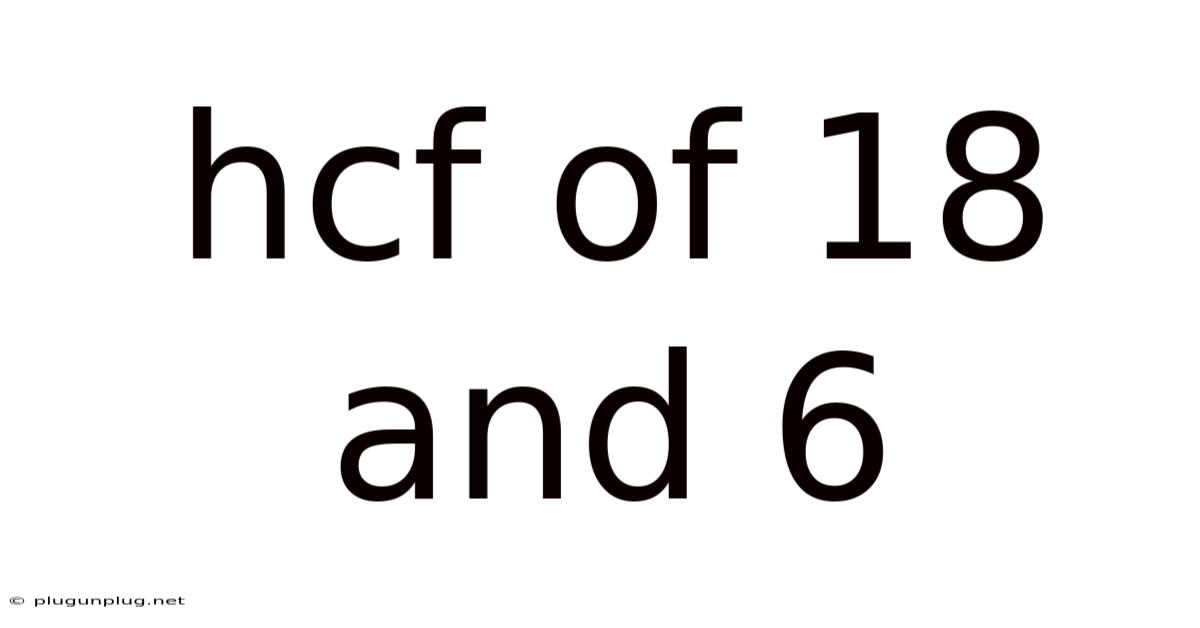
Table of Contents
Unveiling the Mysteries of HCF: A Deep Dive into the Highest Common Factor of 18 and 6
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple task, especially when dealing with relatively small numbers like 18 and 6. However, understanding the underlying principles and different methods for calculating the HCF provides a foundational understanding of number theory and its applications in various fields of mathematics and beyond. This article will delve into the concept of HCF, specifically focusing on finding the HCF of 18 and 6, exploring various methods, and expanding on the broader implications of this seemingly simple calculation.
Introduction: What is the Highest Common Factor (HCF)?
The highest common factor (HCF) of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. It's the biggest number that is a factor of all the given numbers. Think of it as the largest common building block of those numbers. For example, the factors of 18 are 1, 2, 3, 6, 9, and 18. The factors of 6 are 1, 2, 3, and 6. The common factors of 18 and 6 are 1, 2, 3, and 6. The highest of these common factors is 6. Therefore, the HCF of 18 and 6 is 6.
This seemingly simple concept has significant applications in various areas, including simplifying fractions, solving problems related to measurements and proportions, and forming the basis for more advanced mathematical concepts. Understanding HCF is crucial for building a strong foundation in mathematics.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers. To find the HCF of 18 and 6 using this method:
-
List the factors of each number:
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 6: 1, 2, 3, 6
-
Identify the common factors: The numbers that appear in both lists are the common factors: 1, 2, 3, and 6.
-
Determine the highest common factor: The largest number among the common factors is 6. Therefore, the HCF of 18 and 6 is 6.
This method is easy to visualize and understand, making it ideal for introducing the concept of HCF to beginners. However, it becomes less efficient when dealing with larger numbers, as listing all factors can be time-consuming and prone to errors.
Method 2: Prime Factorization
Prime factorization is a more efficient and systematic method for finding the HCF, especially when dealing with larger numbers. This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
-
Find the prime factorization of each number:
- 18 = 2 x 3 x 3 = 2 x 3²
- 6 = 2 x 3
-
Identify common prime factors: Both 18 and 6 share the prime factors 2 and 3.
-
Multiply the common prime factors: The HCF is the product of the common prime factors raised to the lowest power. In this case, we have one 2 and one 3. Therefore, HCF(18, 6) = 2 x 3 = 6.
This method is more efficient than listing factors, especially when dealing with larger numbers. It provides a clear and systematic approach, reducing the chances of error.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, particularly useful for larger numbers. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the HCF.
-
Divide the larger number by the smaller number and find the remainder:
- 18 ÷ 6 = 3 with a remainder of 0.
-
If the remainder is 0, the smaller number is the HCF: Since the remainder is 0, the smaller number, 6, is the HCF. Therefore, HCF(18, 6) = 6.
If the remainder was not 0, we would continue the process by dividing the smaller number by the remainder, and so on, until we reach a remainder of 0. The last non-zero remainder would then be the HCF.
Explanation of the Methods and their Applications
The three methods presented above – listing factors, prime factorization, and the Euclidean algorithm – offer different approaches to finding the HCF. The choice of method depends on the context and the size of the numbers involved.
-
Listing factors: This is suitable for smaller numbers and provides a basic understanding of the concept. It's easy to visualize but becomes less practical for larger numbers.
-
Prime factorization: This is a more efficient and systematic method suitable for larger numbers. It's based on fundamental number theory and provides a clear understanding of the number's structure. It’s particularly useful in more complex HCF problems involving multiple numbers.
-
Euclidean algorithm: This is the most efficient method for larger numbers, particularly when dealing with very large numbers where prime factorization becomes computationally expensive. Its iterative nature makes it suitable for computer algorithms.
The application of HCF extends beyond simple number theory. It’s crucial in:
-
Simplifying fractions: Finding the HCF of the numerator and denominator allows for simplifying a fraction to its lowest terms. For example, the fraction 18/6 can be simplified to 3/1 (or 3) by dividing both numerator and denominator by their HCF, which is 6.
-
Measurement and proportion: HCF is used in solving problems involving measurements where you need to find the largest common unit for measuring. Imagine needing to cut pieces of wood of length 18 cm and 6 cm into identical smaller pieces without any waste. The HCF (6 cm) would determine the length of the largest identical pieces you can cut.
-
Modular arithmetic: HCF plays a critical role in modular arithmetic, a branch of number theory used in cryptography and computer science.
-
Abstract algebra: The concept of GCD extends to more abstract algebraic structures, forming the foundation for concepts like ideals and modules.
Frequently Asked Questions (FAQs)
-
What if the HCF is 1? If the HCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Can I find the HCF of more than two numbers? Yes, the methods described above can be extended to find the HCF of more than two numbers. For example, to find the HCF of 18, 6, and 12, you would find the prime factorization of each number and identify the common prime factors raised to the lowest power.
-
What is the difference between HCF and LCM? The least common multiple (LCM) is the smallest number that is a multiple of all the given numbers. HCF and LCM are related through the following formula for two numbers a and b: LCM(a, b) x HCF(a, b) = a x b.
-
How can I use a calculator to find the HCF? Many calculators have a built-in function for finding the HCF (or GCD). Consult your calculator's manual for instructions on how to use this function.
-
Are there any real-world applications of HCF beyond mathematics? Yes, HCF principles are applied in various fields including music theory (finding common musical intervals), engineering (calculating gear ratios), and computer science (algorithm optimization).
Conclusion: Beyond the Basics of HCF
Finding the HCF of 18 and 6, while seemingly simple, opens a door to a deeper understanding of number theory and its diverse applications. The different methods explored – listing factors, prime factorization, and the Euclidean algorithm – highlight the versatility and importance of this fundamental mathematical concept. Understanding HCF is not just about solving simple arithmetic problems; it's about grasping a core principle that underpins many more complex mathematical and real-world applications. From simplifying fractions to optimizing computer algorithms, the HCF proves its utility far beyond the classroom. By mastering this seemingly simple concept, you're building a strong foundation for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
Round To The Nearest Five
Sep 18, 2025
-
6 5 As A Percentage
Sep 18, 2025
-
How Many Sides On Octagon
Sep 18, 2025
-
Is Fungi Prokaryotic Or Eukaryotic
Sep 18, 2025
-
Difference Between Nhl And Hl
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 18 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.