Integral Of 1 X 3
plugunplug
Sep 20, 2025 · 5 min read
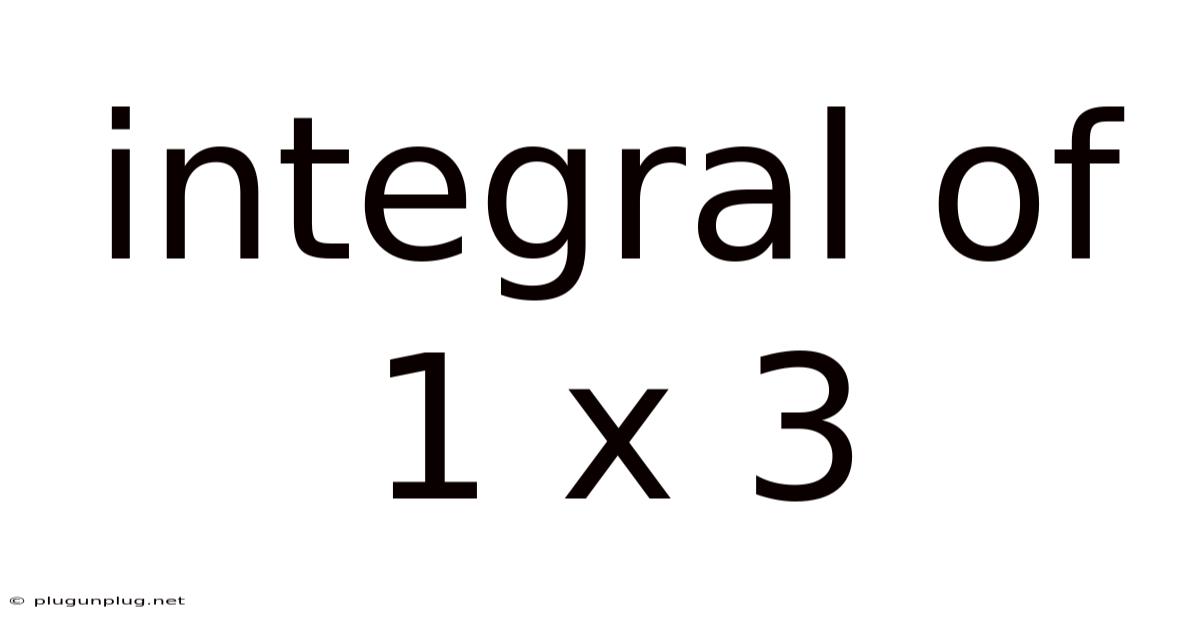
Table of Contents
Understanding and Solving the Integral of 1/(x³): A Comprehensive Guide
The integral of 1/x³, often written as ∫(1/x³)dx, is a fundamental concept in calculus. This seemingly simple problem unlocks a deeper understanding of integration techniques and their applications in various fields, from physics and engineering to economics and computer science. This comprehensive guide will walk you through the solution, exploring the underlying principles and addressing common questions. We'll move beyond a simple answer to provide a solid grasp of the process.
Introduction: Deconstructing the Problem
Before diving into the solution, let's break down the problem itself. We are tasked with finding the indefinite integral of the function f(x) = 1/x³. Remember, an indefinite integral represents a family of functions whose derivatives are equal to the original function. In simpler terms, we're looking for a function whose derivative is 1/x³. This process is the reverse of differentiation. Understanding this fundamental concept is crucial for mastering integration.
The power rule of integration plays a key role here. While seemingly straightforward, applying it correctly requires careful attention to detail, especially when dealing with negative exponents, as we are in this case.
Applying the Power Rule of Integration
The power rule of integration states that the integral of x<sup>n</sup> dx is (x<sup>n+1</sup>)/(n+1) + C, where 'n' is any real number except -1, and 'C' is the constant of integration. This constant accounts for the family of functions that share the same derivative.
In our case, 1/x³ can be rewritten as x<sup>-3</sup>. Now, we can apply the power rule:
∫x<sup>-3</sup> dx = (x<sup>-3+1</sup>)/(-3+1) + C
Simplifying this expression, we get:
∫x<sup>-3</sup> dx = (x<sup>-2</sup>)/(-2) + C
Further simplification leads to our final answer:
∫(1/x³) dx = -1/(2x²) + C
A Deeper Dive: Understanding the Constant of Integration (C)
The constant of integration, 'C', is a crucial element often overlooked by beginners. It represents an arbitrary constant that can take on any real value. Why is it there? Because the derivative of a constant is always zero. Therefore, infinitely many functions can have the same derivative.
For example, consider the functions:
- f(x) = -1/(2x²) + 1
- g(x) = -1/(2x²) + 5
- h(x) = -1/(2x²) - π
The derivatives of all three functions are identical: 1/x³. The constant 'C' accounts for this ambiguity. The indefinite integral represents a family of functions, all differing only by a constant.
To find a specific function within this family, we would need additional information, such as an initial condition (e.g., the value of the function at a particular point). This would allow us to solve for the value of 'C'.
Illustrative Examples: Applying the Integral in Context
Let's consider a few examples to illustrate how this integral might be applied in real-world scenarios.
Example 1: Physics (Coulomb's Law)
Coulomb's Law describes the force between two point charges. The electric field due to a point charge is inversely proportional to the square of the distance. Integrating the electric field to find the electric potential often involves an integral similar to the one we've solved.
Example 2: Engineering (Fluid Mechanics)
In fluid mechanics, the calculation of fluid flow rates and pressures sometimes involves integrals of functions representing inverse powers of distance.
Example 3: Economics (Marginal Cost and Total Cost)
In economics, the marginal cost function represents the additional cost of producing one more unit of a good. The total cost function is the integral of the marginal cost function. While not always involving 1/x³, the concept of integration is fundamental in these calculations.
Common Mistakes and How to Avoid Them
Several common mistakes can arise when tackling this type of integral. Let's address them:
- Forgetting the Constant of Integration (C): This is the most frequent mistake. Always remember to include 'C' in your indefinite integral.
- Incorrect Application of the Power Rule: Carefully watch your exponents, especially when dealing with negative exponents. Remember to add 1 to the exponent and then divide by the new exponent.
- Incorrect Simplification: Double-check your algebraic manipulation. Simple errors can easily creep in.
Frequently Asked Questions (FAQ)
Q: What if the integral was ∫(1/x²) dx?
A: Using the power rule, we would have ∫x<sup>-2</sup> dx = (x<sup>-1</sup>)/(-1) + C = -1/x + C
Q: Can I use numerical methods to solve this integral?
A: While numerical methods like Simpson's rule or the trapezoidal rule are powerful tools for approximating definite integrals, they are not necessary for this indefinite integral. The power rule provides an exact analytical solution.
Q: What is the difference between a definite and an indefinite integral?
A: An indefinite integral, as we've discussed, finds a family of functions whose derivatives are equal to the original function. A definite integral, on the other hand, calculates the area under the curve of a function between two specific limits of integration. It gives a numerical value rather than a function.
Q: What happens when n = -1 in the power rule?
A: The power rule is not valid when n = -1 (i.e., for ∫(1/x) dx). This integral results in the natural logarithm: ln|x| + C. This is a special case that requires a different approach.
Conclusion: Mastering the Fundamentals
Successfully solving the integral of 1/x³ requires a solid understanding of the power rule of integration and a keen attention to detail. Remembering the constant of integration and carefully handling negative exponents are crucial for accuracy. While seemingly a simple problem, this integral serves as a building block for understanding more complex integration techniques and their practical applications in various scientific and engineering disciplines. Practice is key to mastering these fundamental concepts, allowing you to tackle increasingly sophisticated problems with confidence. By understanding not just the solution but the underlying principles, you're building a strong foundation for your future studies in calculus and beyond.
Latest Posts
Latest Posts
-
What Did Jj Thomson Discover
Sep 20, 2025
-
Diagram Of The Tooth Labeled
Sep 20, 2025
-
2 To Power Of 4
Sep 20, 2025
-
Conversion Of Kg To N
Sep 20, 2025
-
Chemical Formula Of Sodium Sulfate
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.