Lcm Of 3 5 6
plugunplug
Sep 20, 2025 · 6 min read
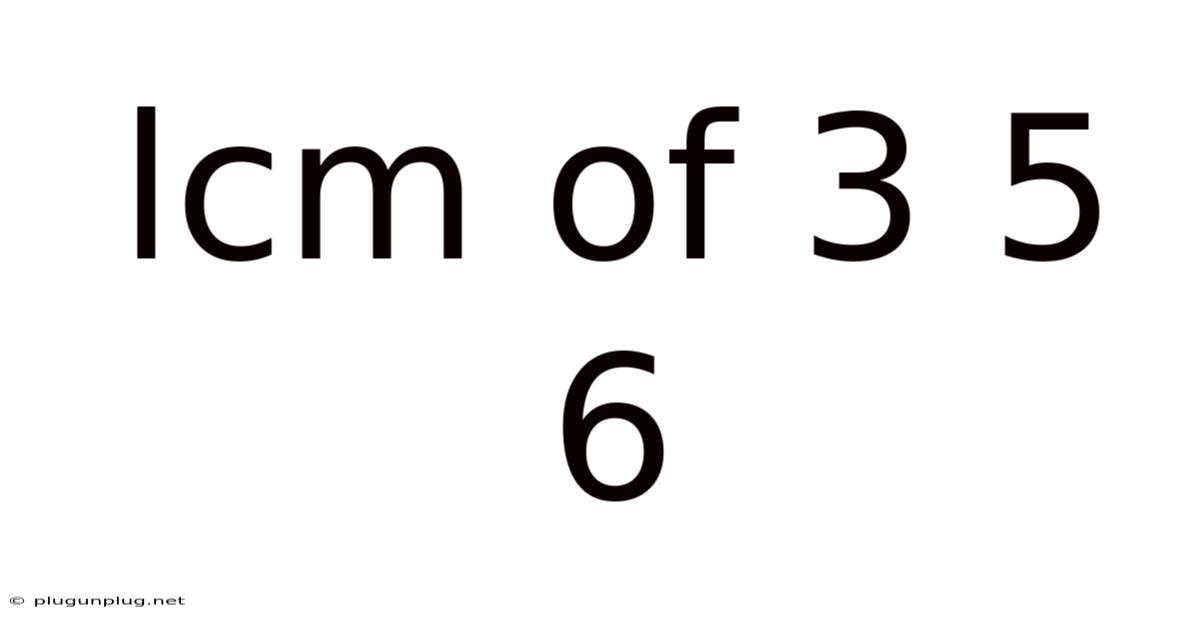
Table of Contents
Finding the LCM of 3, 5, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This article provides a thorough explanation of how to calculate the LCM of 3, 5, and 6, exploring different methods and delving into the underlying mathematical principles. Understanding this seemingly simple calculation unlocks a deeper understanding of number theory and its practical applications. We will cover various methods, address common questions, and provide ample examples to ensure a complete understanding.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's clarify what the least common multiple is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
One of the simplest methods, particularly suitable for smaller numbers like 3, 5, and 6, involves listing the multiples of each number until a common multiple is found.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, ...
- Multiples of 6: 6, 12, 18, 24, 30, ...
By comparing the lists, we can see that the smallest number appearing in all three lists is 30. Therefore, the LCM of 3, 5, and 6 is 30. This method is straightforward but can become cumbersome when dealing with larger numbers or a greater number of integers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
-
Prime Factorization:
- 3 = 3
- 5 = 5
- 6 = 2 x 3
-
Identifying the Highest Powers: We identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Calculating the LCM: To find the LCM, we multiply these highest powers together:
LCM(3, 5, 6) = 2 x 3 x 5 = 30
This method is more systematic and less prone to errors, especially when dealing with larger numbers. It reveals the fundamental structure of the numbers and their relationships.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, but it becomes more complex. For three numbers, a, b, and c, a more general approach using prime factorization is recommended. However, for two numbers, this method can be efficient. Let's illustrate this with an example using two numbers from our set: finding the LCM of 3 and 6.
-
Find the GCD of 3 and 6: The GCD of 3 and 6 is 3 (because 3 is the largest number that divides both 3 and 6 without a remainder).
-
Apply the formula: LCM(3, 6) x GCD(3, 6) = 3 x 6 LCM(3, 6) x 3 = 18 LCM(3, 6) = 18 / 3 = 6
While this method demonstrates the relationship between LCM and GCD, it's less practical for finding the LCM of multiple numbers like 3, 5, and 6. The prime factorization method remains the most efficient for this scenario.
Understanding the Significance of LCM
The LCM is not just a theoretical concept; it finds applications in various real-world situations and mathematical problems. Here are some examples:
- Fraction Addition and Subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator.
- Scheduling Problems: Imagine two buses arrive at a station at different intervals. The LCM helps determine when both buses will arrive at the station simultaneously.
- Cyclic Patterns: The LCM is useful in analyzing repetitive patterns or cycles. For example, determining when two events with different periodicities will coincide.
- Modular Arithmetic: LCM plays a vital role in modular arithmetic, a branch of number theory used in cryptography and computer science.
Frequently Asked Questions (FAQ)
-
What if the numbers have no common factors? If the numbers are relatively prime (meaning they share no common factors other than 1), then their LCM is simply their product. For example, the LCM of 5 and 7 (which are relatively prime) is 5 x 7 = 35.
-
Can I use a calculator to find the LCM? Many scientific calculators and online calculators have built-in functions to calculate the LCM of a set of numbers. Understanding the methods, however, allows you to solve problems even without a calculator.
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the largest common divisor. They are inverse concepts, related by the formula mentioned earlier.
-
Why is the prime factorization method preferred for larger numbers? The prime factorization method is more efficient for larger numbers because it avoids the lengthy process of listing multiples. It provides a structured and systematic approach that is less error-prone.
-
How do I find the LCM of more than three numbers? The prime factorization method is easily extended to handle more than three numbers. You simply factorize each number into its prime factors, identify the highest power of each prime factor present, and then multiply these highest powers together to find the LCM.
Conclusion
Finding the LCM of 3, 5, and 6, whether through listing multiples, prime factorization, or understanding the relationship with GCD, reinforces fundamental mathematical concepts. The prime factorization method emerges as the most efficient and versatile approach, particularly when dealing with larger numbers or more complex scenarios. Mastering the calculation of the LCM unlocks a deeper understanding of number theory and provides essential tools for tackling various mathematical problems in different fields. The ability to calculate LCM is not just about getting the right answer (30 in this case); it's about developing a strong foundation in mathematical reasoning and problem-solving skills – crucial assets in any academic or professional pursuit. Remember to practice using different methods to solidify your understanding and improve your efficiency.
Latest Posts
Latest Posts
-
World Birth And Death Clock
Sep 20, 2025
-
River In S W Asia
Sep 20, 2025
-
What Does Salt Stand For
Sep 20, 2025
-
What Is Matter Made Of
Sep 20, 2025
-
How To Tie Double Windsor
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.