Ln X 2 Lnx 2
plugunplug
Sep 25, 2025 · 7 min read
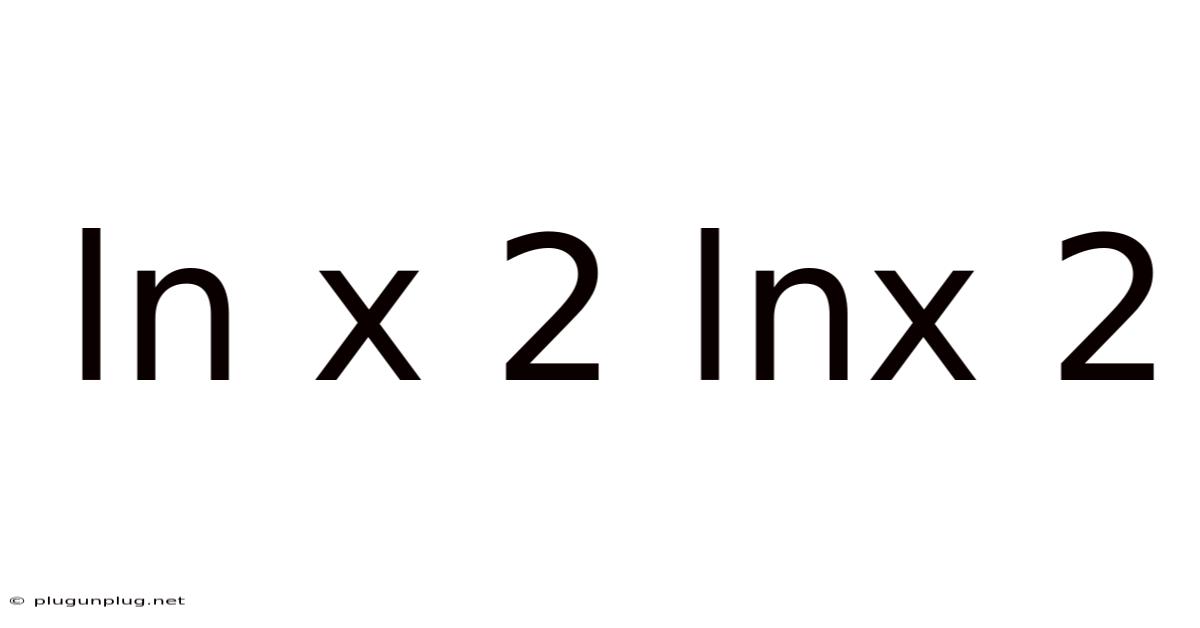
Table of Contents
Delving Deep into ln(x²) and 2ln(x): A Comprehensive Exploration
Understanding logarithmic functions is crucial for anyone delving into mathematics, particularly calculus and its applications in various fields like physics, engineering, and finance. This article focuses on a seemingly simple yet often misunderstood concept: the relationship between ln(x²) and 2ln(x). We'll explore this relationship rigorously, providing a detailed explanation that goes beyond simple formulas and delves into the underlying principles of logarithms. This will equip you with a solid grasp of logarithmic manipulation, essential for more advanced mathematical concepts.
Introduction: Unveiling the Logarithmic World
The natural logarithm, denoted as ln(x), represents the logarithm to the base e, where e is the mathematical constant approximately equal to 2.71828. It's the inverse function of the exponential function e<sup>x</sup>. In simpler terms, ln(x) answers the question: "To what power must e be raised to obtain x?" Understanding this foundational concept is key to grasping the relationship between ln(x²) and 2ln(x). This article will illuminate this relationship, clarifying any potential confusion and providing a solid foundation for further logarithmic exploration.
The Core Relationship: ln(x²) = 2ln(x)
The core of our exploration lies in the logarithmic property that allows us to move exponents from inside the logarithm to become multipliers outside. This is a fundamental property that applies to all logarithms, not just natural logarithms. The equation ln(x²) = 2ln(x) is a direct application of this property. Let's explore why this equality holds true.
Mathematical Proof:
We can derive this equality using the properties of logarithms. Recall the power rule of logarithms: log<sub>b</sub>(a<sup>c</sup>) = c * log<sub>b</sub>(a). Applying this rule to the natural logarithm (where b = e), we get:
ln(x²) = 2 * ln(x)
This straightforward application of the power rule shows the equivalence between ln(x²) and 2ln(x). It's crucial to understand that this equality holds only for positive values of x, as the natural logarithm is undefined for non-positive numbers.
Intuitive Understanding:
Let's approach this intuitively. Remember that ln(x) represents the exponent to which e must be raised to get x. Therefore, ln(x²) represents the exponent to which e must be raised to obtain x². However, x² is equivalent to x*x, or x raised to the power of 2. Using the property of exponents, we can rewrite e raised to the power of ln(x²) as (e<sup>ln(x)</sup>)². Since e<sup>ln(x)</sup> simplifies to x, the expression becomes x². This confirms the equivalence to 2ln(x).
Practical Applications and Examples
The relationship ln(x²) = 2ln(x) is not just a theoretical curiosity; it's a powerful tool with many practical applications in various mathematical contexts. Let's explore some examples:
1. Simplification of Logarithmic Expressions:
This property is invaluable for simplifying complex logarithmic expressions. Consider the expression ln( (x³y²) / z). Using logarithm properties, we can rewrite this as:
ln(x³) + ln(y²) - ln(z) = 3ln(x) + 2ln(y) - ln(z)
This simplified form is often easier to work with in calculus or when solving equations.
2. Solving Equations:
The property ln(x²) = 2ln(x) is often crucial in solving logarithmic equations. Consider the equation:
ln(x²) + ln(x) = 6
Using the property, we can simplify this to:
2ln(x) + ln(x) = 6 3ln(x) = 6 ln(x) = 2 x = e²
This demonstrates how the property enables efficient solutions to complex logarithmic equations.
3. Calculus Applications:
Differentiation and integration involving logarithmic functions often benefit from the application of this property. For example, consider finding the derivative of f(x) = ln(x²). Using the chain rule and the property, we can find a simplified solution:
f'(x) = (1/x²) * 2x = 2/x
Alternatively, using the property first:
f(x) = 2ln(x) f'(x) = 2(1/x) = 2/x
Both methods yield the same result, highlighting the efficacy of utilizing ln(x²) = 2ln(x) for simplification in calculus.
4. Real-world applications:
The natural logarithm and its properties find extensive use in various fields. For example:
- Growth and Decay: Many natural processes, like population growth or radioactive decay, are modeled using exponential functions, and their analysis frequently involves logarithms.
- Finance: Compound interest calculations and present value computations frequently use logarithmic functions.
- Physics: Logarithmic scales are used in various physics applications, like measuring sound intensity (decibels) or earthquake magnitude (Richter scale). Understanding logarithmic manipulations is crucial for interpreting these scales accurately.
Beyond the Basics: Exploring Related Concepts
While ln(x²) = 2ln(x) is a fundamental relationship, it's important to explore related concepts and potential misconceptions to build a comprehensive understanding.
1. The Domain of Definition:
It’s crucial to remember that the natural logarithm is only defined for positive real numbers. Therefore, the equality ln(x²) = 2ln(x) only holds true when x > 0. Attempting to apply this rule to negative values of x will lead to incorrect results.
2. Extension to Other Logarithms:
The power rule of logarithms, which underlies the relationship ln(x²) = 2ln(x), is applicable to logarithms of any base. For instance, log<sub>10</sub>(x²) = 2log<sub>10</sub>(x).
3. Logarithmic Differentiation:
In calculus, the ability to simplify logarithmic expressions is often crucial. The property ln(x²) = 2ln(x) can significantly simplify logarithmic differentiation, making the process more manageable and less error-prone.
4. Solving Inequalities:
Understanding this property can simplify the solving of logarithmic inequalities. The technique involves careful manipulation, ensuring that the inequality remains valid under the transformations, keeping in mind the domain restriction of the natural logarithm.
Frequently Asked Questions (FAQ)
Q1: Is ln(x²) the same as (ln(x))²?
A1: No, ln(x²) is not the same as (ln(x))². ln(x²) = 2ln(x), while (ln(x))² represents the square of the natural logarithm of x. These are distinct mathematical expressions.
Q2: Can I use this property for any logarithmic base?
A2: Yes, the power rule of logarithms (log<sub>b</sub>(a<sup>c</sup>) = c * log<sub>b</sub>(a)) applies to logarithms with any base b (where b > 0 and b ≠ 1). Therefore, the principle extends beyond the natural logarithm.
Q3: What happens if x is negative?
A3: The natural logarithm is undefined for negative numbers. Therefore, the equation ln(x²) = 2ln(x) is not valid when x is negative. Attempting to apply it will result in an undefined expression.
Q4: How does this relate to exponential functions?
A4: The natural logarithm and the exponential function are inverse functions of each other. This inverse relationship is fundamental to understanding the properties of logarithms and allows for efficient manipulation between exponential and logarithmic forms. Understanding this inverse relationship is key to solving many problems involving both exponential and logarithmic functions.
Conclusion: Mastering Logarithmic Manipulation
The relationship between ln(x²) and 2ln(x) is more than just a mathematical identity; it’s a fundamental concept that underscores the power and elegance of logarithmic properties. Mastering this relationship, along with other logarithmic rules, is crucial for success in various mathematical disciplines and their applications. By understanding both the mathematical proof and the intuitive reasoning behind the equality ln(x²) = 2ln(x), you will be well-equipped to tackle more advanced mathematical problems involving logarithmic functions. Remember to always check the domain of the logarithmic functions, ensuring you are working with valid mathematical expressions. The ability to simplify complex logarithmic expressions and to solve equations and inequalities involving them will significantly enhance your problem-solving abilities in various fields. This knowledge provides a robust foundation for tackling more advanced mathematical concepts and unlocking a deeper understanding of the natural world.
Latest Posts
Latest Posts
-
How Many Grams In 2kg
Sep 25, 2025
-
Ethanoic Acid With Sodium Hydroxide
Sep 25, 2025
-
1 3 4 As Improper Fraction
Sep 25, 2025
-
Where Is Wernickes Area Located
Sep 25, 2025
-
What Is 10 Of 25
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Ln X 2 Lnx 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.