M Y2 Y1 X2 X1
plugunplug
Sep 25, 2025 · 7 min read
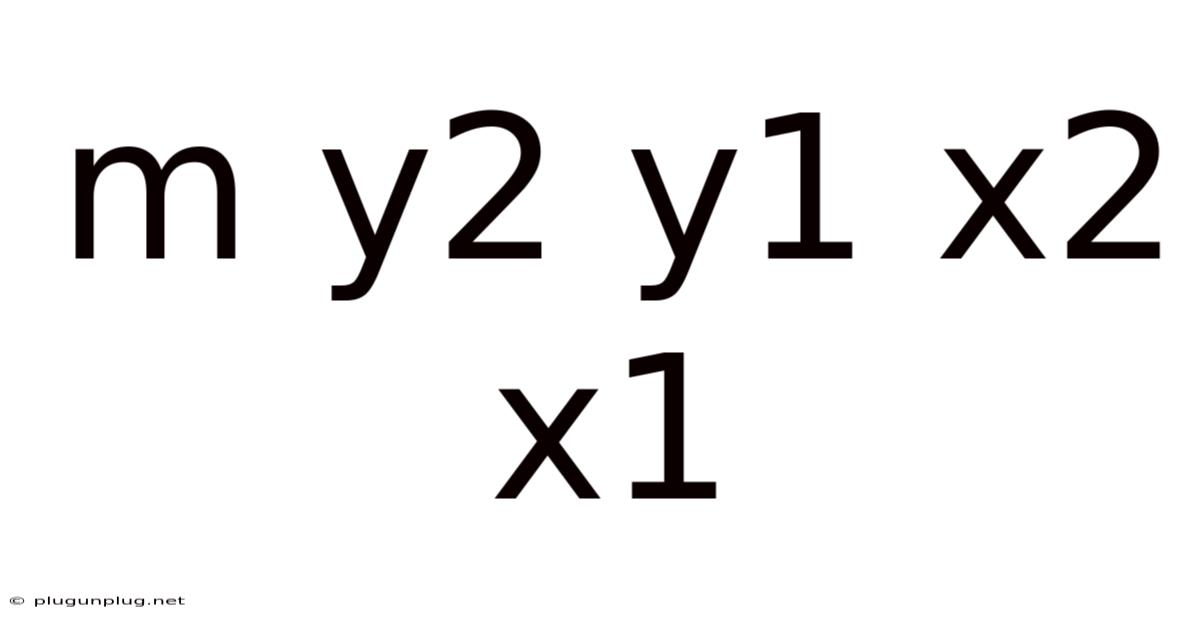
Table of Contents
Understanding the Significance of (y2 - y1) / (x2 - x1): Slope and its Applications
The expression (y2 - y1) / (x2 - x1) is a fundamental concept in mathematics, specifically in algebra and calculus. It represents the slope of a line passing through two points (x1, y1) and (x2, y2) on a Cartesian coordinate system. Understanding this formula is crucial for various applications, from calculating the steepness of a hill to predicting future trends in data analysis. This article will delve into the meaning, calculation, applications, and significance of this crucial mathematical expression.
Introduction to Slope
The slope of a line is a measure of its steepness. It describes how much the y-value changes for every unit change in the x-value. A positive slope indicates an upward trend (as x increases, y increases), a negative slope indicates a downward trend (as x increases, y decreases), and a slope of zero indicates a horizontal line (no change in y as x changes). An undefined slope indicates a vertical line (infinite change in y for a small change in x).
The formula (y2 - y1) / (x2 - x1) provides a precise way to calculate this steepness. Let's break down each component:
- (y2 - y1): This represents the rise or the vertical change between the two points. It's the difference in the y-coordinates.
- (x2 - x1): This represents the run or the horizontal change between the two points. It's the difference in the x-coordinates.
- (/): This division operation gives us the ratio of the rise to the run, representing the slope, often denoted as 'm'. Therefore, m = (y2 - y1) / (x2 - x1).
Calculating the Slope: A Step-by-Step Guide
Let's illustrate the calculation of the slope with a few examples. Remember, it's crucial to maintain consistency; subtract the coordinates in the same order for both x and y.
Example 1: Find the slope of the line passing through points A(2, 3) and B(5, 9).
- Identify the coordinates: (x1, y1) = (2, 3) and (x2, y2) = (5, 9).
- Apply the formula: m = (9 - 3) / (5 - 2) = 6 / 3 = 2.
- Interpret the result: The slope is 2. This means for every 1 unit increase in x, y increases by 2 units. The line has a positive slope, indicating an upward trend.
Example 2: Find the slope of the line passing through points C(-1, 4) and D(3, -2).
- Identify the coordinates: (x1, y1) = (-1, 4) and (x2, y2) = (3, -2).
- Apply the formula: m = (-2 - 4) / (3 - (-1)) = -6 / 4 = -3/2 = -1.5.
- Interpret the result: The slope is -1.5. This means for every 1 unit increase in x, y decreases by 1.5 units. The line has a negative slope, indicating a downward trend.
Example 3: Find the slope of the line passing through points E(4, 2) and F(4, 7).
- Identify the coordinates: (x1, y1) = (4, 2) and (x2, y2) = (4, 7).
- Apply the formula: m = (7 - 2) / (4 - 4) = 5 / 0.
- Interpret the result: The slope is undefined. This is because the line is vertical.
The Equation of a Line: Slope-Intercept Form
Once you know the slope (m) and the y-intercept (b, the point where the line crosses the y-axis), you can write the equation of the line in slope-intercept form: y = mx + b. The y-intercept can be found by substituting one of the points into the equation and solving for b.
Applications of Slope in Real-World Scenarios
The concept of slope extends far beyond theoretical mathematics. Its applications are prevalent in diverse fields:
- Engineering and Construction: Calculating the grade of a road, the incline of a ramp, or the angle of a roof all involve using the slope formula. Understanding slope is critical for ensuring structural stability and safety.
- Physics: Slope is used extensively in physics to describe velocity (change in distance over time), acceleration (change in velocity over time), and gradients in fields like electromagnetism.
- Economics: The slope of a demand or supply curve illustrates the relationship between price and quantity. Economists use slope to understand market trends and predict future changes.
- Data Analysis and Machine Learning: Regression analysis relies heavily on the concept of slope to model the relationship between variables. Predictive models often use linear regression, which directly involves calculating slopes to establish trends and make forecasts.
- Computer Graphics: Slope is crucial in computer graphics for defining the orientation of lines and surfaces. It's fundamental to creating realistic and accurate 2D and 3D visualizations.
- Geography: Topographic maps use contour lines to represent elevation changes. The steepness of the terrain between contour lines is essentially represented by the slope.
- Finance: In financial modelling, slope analysis can be used to assess the performance of assets, identify trends, and develop investment strategies. For example, the slope of a stock price chart can provide insight into the stock's momentum.
Beyond Linear Relationships: Extensions and Limitations
While (y2 - y1) / (x2 - x1) directly calculates the slope of a straight line, the concept of a "rate of change" extends to more complex functions. In calculus, the derivative of a function provides a generalized concept of slope, measuring the instantaneous rate of change at any point on a curve. This allows us to analyze the slope of non-linear relationships.
However, the basic slope formula has its limitations. It only applies to linear relationships – situations where the relationship between x and y can be represented by a straight line. For curved lines or more complex functions, more advanced mathematical tools like calculus are needed to analyze the rate of change.
Frequently Asked Questions (FAQ)
Q1: What if x2 - x1 = 0?
A1: If x2 - x1 = 0, it means the two points have the same x-coordinate, resulting in a vertical line. The slope is undefined in this case, as division by zero is not defined in mathematics.
Q2: Can the slope be zero?
A2: Yes, the slope can be zero. This happens when y2 - y1 = 0, meaning the two points have the same y-coordinate, resulting in a horizontal line. A zero slope indicates no change in the y-value as the x-value changes.
Q3: Is the order of the points important?
A3: While the order of the points doesn't affect the magnitude of the slope, it does affect the sign. If you switch (x1, y1) and (x2, y2), you'll get the same numerical value for the slope, but the sign might change. Consistent subtraction is key.
Q4: How does slope relate to the angle of inclination?
A4: The slope 'm' is related to the angle of inclination (θ) of the line with the positive x-axis through the trigonometric function: m = tan(θ). This means the slope is the tangent of the angle the line makes with the horizontal axis.
Q5: What are some common mistakes to avoid when calculating slope?
A5: Common mistakes include: * Incorrectly subtracting the coordinates (remember to maintain consistency). * Forgetting the order of operations (subtraction before division). * Misinterpreting the sign of the slope (positive indicates upward trend, negative indicates downward trend).
Conclusion: The Enduring Importance of Slope
The simple yet powerful expression (y2 - y1) / (x2 - x1) forms the foundation for understanding linear relationships and rates of change. Its applications extend across various disciplines, highlighting the fundamental role it plays in modeling real-world phenomena. While it might seem like a basic concept, mastering the calculation and interpretation of slope is essential for anyone pursuing studies or careers in mathematics, science, engineering, or data-driven fields. Understanding slope provides a crucial lens through which we can analyze data, predict trends, and make informed decisions based on the relationship between variables. This knowledge empowers us to interpret the world around us more effectively, from the steepness of a mountain to the fluctuations of a stock market.
Latest Posts
Latest Posts
-
Where Do Tsunamis Usually Occur
Sep 25, 2025
-
Articulating Bones In The Shoulder
Sep 25, 2025
-
Nth Term Of A Sequence
Sep 25, 2025
-
Mass Of The Alpha Particle
Sep 25, 2025
-
Elevation Salt Lake City Utah
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about M Y2 Y1 X2 X1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.