Simplify X 2 X 3
plugunplug
Sep 17, 2025 · 5 min read
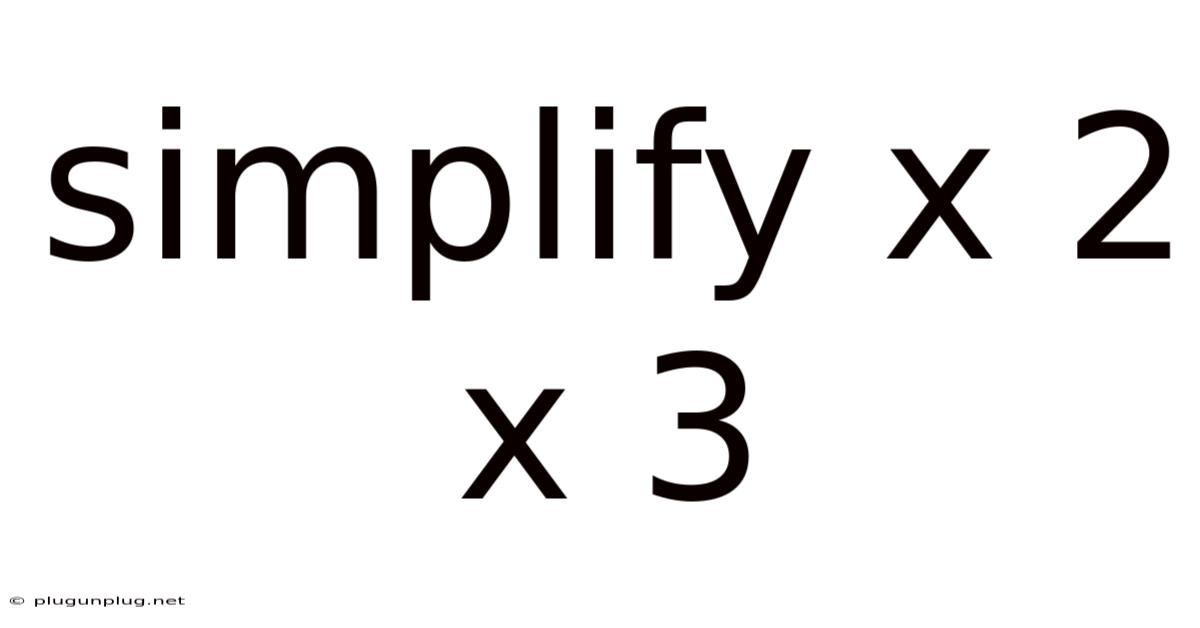
Table of Contents
Simplifying x² x ³: A Deep Dive into Algebraic Multiplication
Understanding how to simplify algebraic expressions is fundamental to success in mathematics, particularly in algebra and beyond. This article will delve into the seemingly simple problem of simplifying x² x ³, providing a comprehensive explanation that goes beyond the immediate answer. We'll explore the underlying principles of exponents, offer practical examples, and address common misconceptions to build a robust understanding of this crucial algebraic concept. This will equip you with the skills to tackle more complex algebraic manipulations confidently.
Understanding Exponents
Before tackling the simplification of x² x ³, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For instance:
x²meansx * x(x multiplied by itself twice).x³meansx * x * x(x multiplied by itself three times).x⁴meansx * x * x * x(x multiplied by itself four times), and so on.
The Product Rule of Exponents
The core principle governing the simplification of x² x ³ is the product rule of exponents. This rule states that when multiplying two terms with the same base and different exponents, you add the exponents while keeping the base the same. Mathematically, this is represented as:
xᵐ * xⁿ = xᵐ⁺ⁿ
Where:
- 'x' is the base (any variable or number).
- 'm' and 'n' are the exponents (any real numbers).
Simplifying x² x ³: A Step-by-Step Approach
Now, let's apply the product rule to simplify x² x ³:
-
Identify the Base and Exponents: In the expression
x² x ³, the base is 'x', and the exponents are 2 and 3. -
Apply the Product Rule: According to the product rule, we add the exponents: 2 + 3 = 5.
-
Write the Simplified Expression: The simplified expression is therefore x⁵. This means
x * x * x * x * x.
Visualizing the Simplification
To further solidify your understanding, let's visualize the multiplication:
x² x ³ = (x * x) * (x * x * x) = x * x * x * x * x = x⁵
Expanding the Concept: More Complex Examples
The product rule applies to more complex expressions as well. Let's consider a few examples:
-
Example 1: Simplify
2x³ * 5x⁴First, multiply the coefficients (the numbers in front of the variables): 2 * 5 = 10. Then, apply the product rule to the variables: x³ * x⁴ = x⁷. Therefore, the simplified expression is 10x⁷.
-
Example 2: Simplify
(3y²)² * y⁵First, simplify the term with the parentheses using the power of a product rule: (3y²)² = 3² * (y²)² = 9y⁴. Then multiply this result by y⁵: 9y⁴ * y⁵ = 9y⁹. The simplified expression is 9y⁹.
-
Example 3: Simplify
a²b³ * a⁴bHere, we have two different variables, but the product rule still applies to each separately. For 'a': a² * a⁴ = a⁶. For 'b': b³ * b¹ = b⁴. Therefore, the simplified expression is a⁶b⁴.
Addressing Common Misconceptions
Several common misconceptions can arise when dealing with exponents. Let's clarify these:
-
Misconception 1: Multiplying Exponents Instead of Adding: A frequent error is multiplying the exponents instead of adding them when using the product rule. Remember, the product rule dictates addition, not multiplication, of the exponents.
-
Misconception 2: Changing the Base: The base remains unchanged during the simplification process; only the exponents are affected. For example,
2x² * 3x³simplifies to6x⁵, not6x⁶or some other variation of the base. -
Misconception 3: Ignoring Coefficients: Coefficients are multiplied normally before applying the exponent rules to the variables. Do not forget to handle coefficients separately during simplification.
The Quotient Rule: A Related Concept
While the focus here is on the product rule, it's beneficial to briefly mention the quotient rule of exponents. This rule governs the division of terms with the same base and different exponents. It states:
xᵐ / xⁿ = xᵐ⁻ⁿ
In this case, we subtract the exponents. For example, x⁵ / x² = x³.
Practical Applications and Real-World Relevance
Understanding exponent rules, and specifically the simplification of expressions like x² x ³, has broad applications across numerous fields. These include:
-
Physics: Calculating areas, volumes, and other physical quantities often involve manipulating exponents.
-
Engineering: Designing structures and systems relies heavily on algebraic manipulations, including exponent rules.
-
Computer Science: Algorithms and data structures often utilize exponential growth and decay models.
-
Finance: Compound interest calculations depend on understanding exponential growth.
Frequently Asked Questions (FAQ)
Q1: What if the bases are different?
A1: The product rule only applies when the bases are the same. If the bases are different (e.g., x² * y³), the expression cannot be simplified further.
Q2: Can I use the product rule with negative exponents?
A2: Yes, the product rule works perfectly with negative exponents. For instance: x⁻² * x³ = x¹ = x.
Q3: What if there are multiple variables with different exponents?
A3: Apply the product rule to each variable separately. For example, a³b²c * a²bc⁴ = a⁵b³c⁵.
Q4: What happens if one of the exponents is zero?
A4: Any base raised to the power of zero is equal to 1 (except for 0⁰, which is undefined). For example, x⁰ = 1. Therefore, x² * x⁰ = x² * 1 = x².
Conclusion
Simplifying x² x ³ to x⁵ is more than just a simple algebraic manipulation; it's a gateway to understanding the fundamental principles of exponents and their applications in numerous mathematical and scientific contexts. Mastering the product rule of exponents is crucial for tackling more advanced algebraic problems, laying a strong foundation for success in higher-level mathematics and related disciplines. By understanding the underlying principles, visualizing the multiplication, and practicing with various examples, you can confidently navigate the world of algebraic simplification and unlock a deeper appreciation for the power and elegance of mathematics. Remember to practice regularly, and don’t hesitate to revisit these concepts as needed to reinforce your understanding. The journey to mathematical fluency is built on consistent effort and a willingness to explore.
Latest Posts
Latest Posts
-
I Am Called In Spanish
Sep 17, 2025
-
What Does Ppa Stand For
Sep 17, 2025
-
What Is The Unit Pascal
Sep 17, 2025
-
How Did The Oceans Form
Sep 17, 2025
-
Scientific Name For A Sloth
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Simplify X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.