What Is 20 Of 100
plugunplug
Sep 21, 2025 · 5 min read
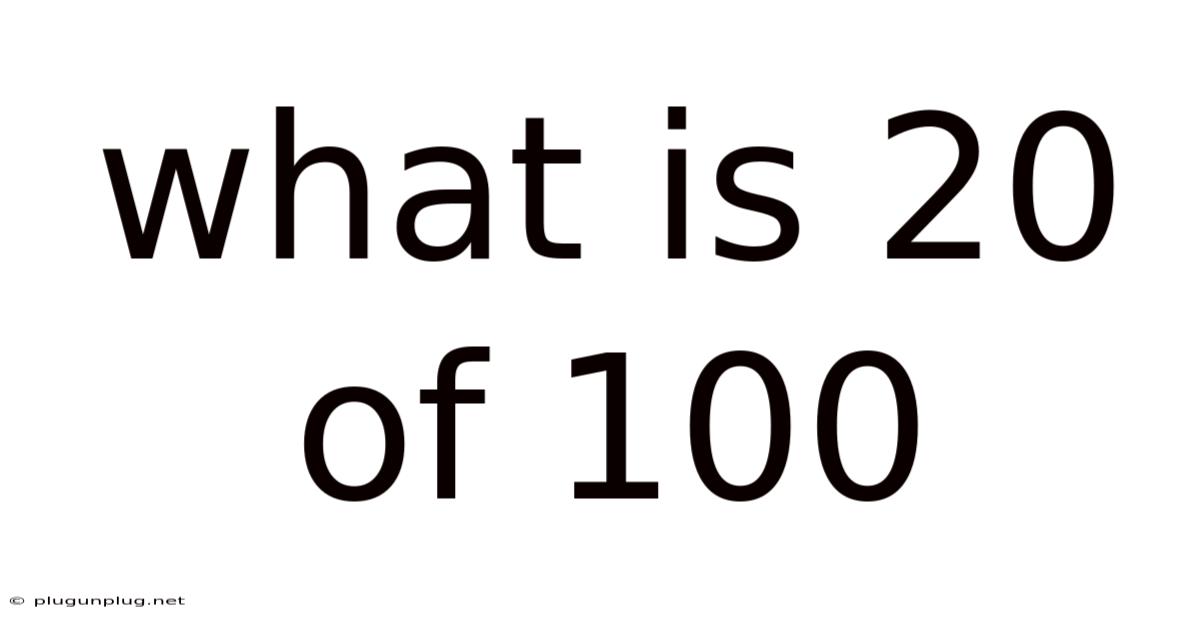
Table of Contents
What is 20 of 100? Understanding Percentages and Fractions
This article explores the seemingly simple question, "What is 20 of 100?", delving beyond the immediate answer to provide a comprehensive understanding of percentages, fractions, and their applications in everyday life. We'll uncover the underlying mathematical principles and demonstrate how this seemingly basic concept forms the foundation for more complex calculations. Understanding this fundamental relationship is crucial for everything from calculating discounts to comprehending statistical data.
Understanding the Basic Calculation: 20/100
At its core, "20 of 100" represents a fraction: 20/100. This fraction signifies that we have 20 parts out of a total of 100 equal parts. This is a fundamental concept in mathematics and forms the basis for understanding percentages. Simply put, 20 out of 100 is 20% (twenty percent).
This calculation is straightforward: Divide 20 by 100: 20 ÷ 100 = 0.2. To express this as a percentage, we multiply the decimal by 100 and add the "%" symbol: 0.2 x 100 = 20%.
Percentages: A Powerful Tool for Comparison and Representation
Percentages provide a standardized way to represent parts of a whole. They are incredibly useful because they allow for easy comparison across different datasets, even if the total quantities are vastly different. Imagine comparing sales figures for two different stores; one might have sold 20 items out of 100, while the other sold 50 items out of 250. While the raw numbers differ, both represent the same percentage: 20%.
The percentage system makes comparisons clear and concise. It removes the need for complex calculations to determine which store performed relatively better. This standardization is vital in various fields, including:
- Business and Finance: Calculating profit margins, interest rates, discounts, and sales growth.
- Science: Representing experimental results, statistical probabilities, and error margins.
- Everyday Life: Understanding discounts at stores, calculating tips, and interpreting survey data.
Fractions: The Building Blocks of Percentages
The fraction 20/100 is equivalent to 20%, but it's also reducible to a simpler fraction. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator (20) and the denominator (100). The GCD of 20 and 100 is 20. Dividing both the numerator and the denominator by 20, we get:
20 ÷ 20 / 100 ÷ 20 = 1/5
This means that 20 out of 100 is the same as 1 out of 5. Understanding this equivalence is crucial because it shows how different mathematical representations can express the same quantity. This ability to convert between fractions, decimals, and percentages is essential for solving a wide range of problems.
Beyond the Basics: Applying the Concept
The concept of "20 of 100" or 20% isn't limited to simple calculations. It's a fundamental building block for more complex scenarios. Let's explore some examples:
1. Calculating Discounts: If a store offers a 20% discount on an item priced at $100, the discount amount is calculated as:
$100 x 0.20 = $20
The final price after the discount would be:
$100 - $20 = $80
2. Determining Percentages in Larger Sets: If a school has 1000 students, and 200 of them are in the tenth grade, the percentage of tenth-grade students is:
200/1000 = 0.20 = 20%
3. Understanding Proportions: The ratio 20:100 represents a proportion. This can be applied to scaling recipes, understanding map scales, or solving problems involving direct proportionality. For instance, if a recipe calls for 20 grams of sugar for every 100 grams of flour, you can easily scale the recipe up or down by maintaining this 20:100 ratio.
Working with Percentages: Common Calculations
Here are some common percentage calculations:
- Finding a percentage of a number: Multiply the number by the percentage (expressed as a decimal). For example, 20% of 500 is 500 x 0.20 = 100.
- Finding the percentage one number is of another: Divide the first number by the second number, and then multiply by 100 to express it as a percentage. For example, to find what percentage 20 is of 50, we do (20/50) x 100 = 40%.
- Increasing a number by a percentage: Multiply the number by (1 + the percentage as a decimal). For example, increasing 500 by 20% is 500 x (1 + 0.20) = 600.
- Decreasing a number by a percentage: Multiply the number by (1 - the percentage as a decimal). For example, decreasing 500 by 20% is 500 x (1 - 0.20) = 400.
The Importance of Context and Accuracy
While the calculation of "20 of 100" is straightforward, the interpretation and application of this percentage depend entirely on the context. Accuracy is also paramount. Rounding errors in percentage calculations can significantly impact results, particularly in financial or scientific applications. Always strive for precision and double-check your calculations.
Frequently Asked Questions (FAQ)
Q: What is the difference between a fraction and a percentage?
A: Both fractions and percentages represent parts of a whole. A fraction expresses this relationship as a ratio (e.g., 20/100), while a percentage expresses it as a number out of 100 (e.g., 20%). They are interchangeable; a fraction can be converted to a percentage and vice versa.
Q: How do I convert a fraction to a percentage?
A: Divide the numerator of the fraction by the denominator and then multiply the result by 100. Add the "%" symbol to indicate it's a percentage.
Q: How do I convert a percentage to a fraction?
A: Divide the percentage by 100 and express the result as a fraction. Simplify the fraction if possible.
Q: What if I have a percentage that is not easily converted to a simple fraction?
A: You can leave it as a decimal or use a calculator to find its approximate fractional representation. For example, 33.33% is approximately 1/3.
Q: Are there any online tools to help with percentage calculations?
A: Yes, many online calculators are readily available to perform various percentage calculations, simplifying the process.
Conclusion: Mastering the Fundamentals
Understanding "what is 20 of 100" transcends a simple arithmetic problem. It's about grasping the fundamental concepts of fractions, percentages, and their versatile applications. This seemingly basic concept is the cornerstone of numerous mathematical operations and is vital for interpreting data, making informed decisions, and excelling in various fields. By mastering these fundamental principles, you equip yourself with a crucial skillset that extends far beyond the classroom. Remember to practice these concepts regularly to build confidence and fluency in percentage calculations. The more you practice, the more comfortable and proficient you will become in applying them to real-world problems.
Latest Posts
Latest Posts
-
First Five Digits Of Pi
Sep 21, 2025
-
Hashemite Kingdom Of Jordan History
Sep 21, 2025
-
X 4 X 1 2
Sep 21, 2025
-
Cooking Green Beans In Microwave
Sep 21, 2025
-
Melting Point Of Benzoic Acid
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.