What Is 25 Of 30
plugunplug
Sep 19, 2025 · 6 min read
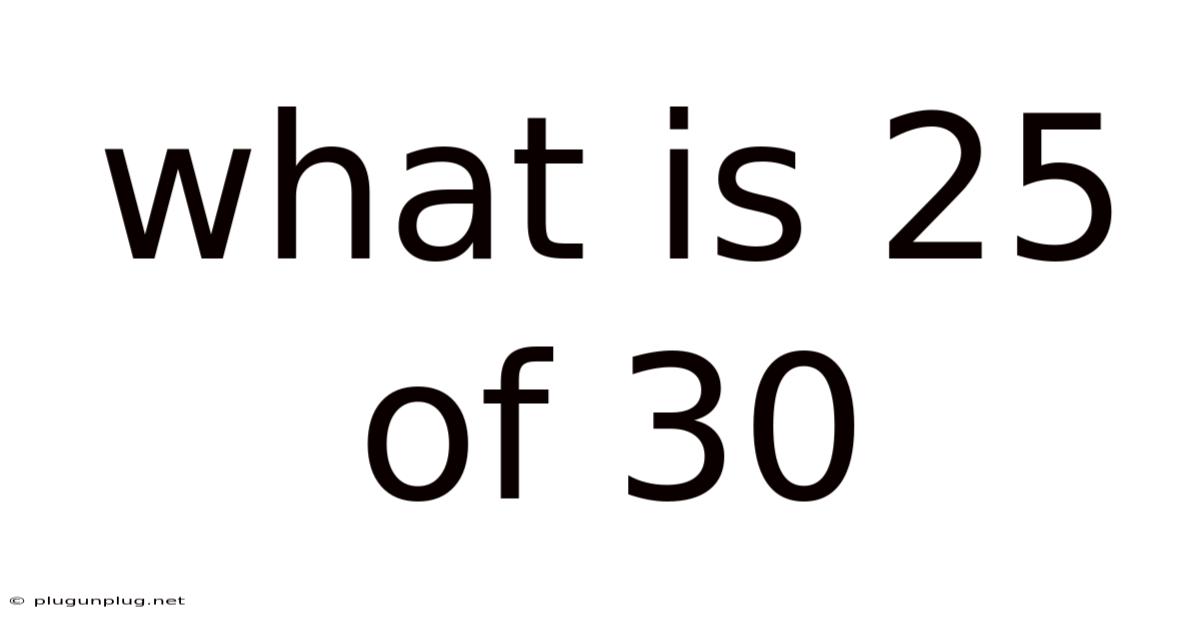
Table of Contents
What is 25 of 30? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 25 of 30?", opens the door to a broader understanding of fundamental mathematical concepts. It's more than just a simple calculation; it's an opportunity to explore fractions, percentages, and ratios, concepts crucial in various aspects of life, from everyday budgeting to advanced scientific calculations. This article will guide you through different methods to solve this problem and delve into the underlying mathematical principles.
Introduction: Deconstructing the Question
The question "What is 25 of 30?" implies finding a portion, or fraction, of a whole. The number 30 represents the whole, and 25 represents the part we're interested in. We can interpret this question in several ways, leading to different approaches to finding the solution. We'll examine these approaches, highlighting the relationship between fractions, percentages, and ratios. This exploration will also touch upon the practical application of these concepts in various fields.
Method 1: Using Fractions
The most straightforward approach is to interpret "25 of 30" as a fraction. In this context, it translates to 25/30. This fraction represents the ratio of the part (25) to the whole (30).
To simplify this fraction, we find the greatest common divisor (GCD) of 25 and 30. The GCD of 25 and 30 is 5. Dividing both the numerator (25) and the denominator (30) by 5, we get:
25/30 = 5/6
Therefore, 25 of 30 is equivalent to 5/6. This fraction represents the portion of 30 that 25 constitutes.
Method 2: Converting to a Percentage
Fractions can be easily converted to percentages, providing another way to express the relationship between 25 and 30. To convert the fraction 5/6 to a percentage, we perform the following calculation:
(5/6) * 100% = 83.333...%
This means that 25 is approximately 83.33% of 30. The recurring decimal indicates that the percentage is not perfectly represented; it's an approximation. In practical applications, rounding this to 83.33% is often sufficient.
Method 3: Using Ratios
The relationship between 25 and 30 can also be expressed as a ratio. A ratio shows the proportional relationship between two or more quantities. The ratio of 25 to 30 is written as 25:30. Similar to the fraction, we can simplify this ratio by dividing both numbers by their GCD (5):
25:30 = 5:6
This simplified ratio, 5:6, conveys the same information as the fraction 5/6 – that 25 represents 5 parts out of a total of 6 parts. Ratios are frequently used in various fields, such as scaling recipes, mixing ingredients, and comparing different quantities.
Understanding the Concepts: A Deeper Dive
Now that we've solved the problem using different methods, let's delve into a more profound understanding of the underlying concepts:
-
Fractions: A fraction represents a part of a whole. It's composed of a numerator (the top number, representing the part) and a denominator (the bottom number, representing the whole). Understanding fractions is fundamental to arithmetic, algebra, and many other mathematical disciplines.
-
Percentages: A percentage is a way of expressing a fraction as a portion of 100. It's often used to represent proportions, changes, or rates. For instance, 83.33% indicates that something constitutes 83.33 parts out of 100 parts. Percentages are commonly used in finance, statistics, and everyday life.
-
Ratios: A ratio is a comparison of two or more quantities. It shows the relative size of one quantity to another. Ratios are often expressed using a colon (:) or as a fraction. They are widely used in scaling, comparing proportions, and solving various problems in different fields.
-
Greatest Common Divisor (GCD): The GCD is the largest number that divides two or more integers without leaving a remainder. Finding the GCD is crucial for simplifying fractions and ratios, making them easier to understand and work with. Different methods exist to find the GCD, including the Euclidean algorithm.
Practical Applications
The concepts of fractions, percentages, and ratios are not just abstract mathematical ideas; they have numerous practical applications in various aspects of our lives. Here are a few examples:
-
Finance: Calculating interest rates, discounts, profit margins, and budgeting all involve using fractions and percentages.
-
Cooking: Scaling recipes up or down requires understanding ratios and proportions.
-
Science: Many scientific calculations, particularly those involving proportions and concentrations, rely heavily on fractions and ratios.
-
Engineering: Designing structures, calculating forces, and analyzing systems often involve working with ratios and proportions.
-
Data Analysis: Percentages and ratios are fundamental for interpreting data, analyzing trends, and drawing conclusions from statistical information.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve "25 of 30"?
A: Absolutely! You can use a calculator to perform the division 25/30 directly, and then multiply by 100% to get the percentage. Many calculators also have features for simplifying fractions.
Q: What if the numbers were larger or more complex?
A: The same principles apply. You would still use fractions, percentages, or ratios to represent the relationship between the parts and the whole. For larger numbers, a calculator can be a helpful tool.
Q: Are there other ways to express "25 of 30"?
A: Yes, you could use decimal representation. The decimal equivalent of 5/6 is approximately 0.8333. You could also express it using a different ratio, such as 10:12 or 15:18, which are equivalent to 5:6.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. A simplified fraction provides the most concise representation of the relationship between the numerator and denominator.
Q: What are some common mistakes to avoid when working with fractions, percentages, and ratios?
A: Common mistakes include incorrect simplification of fractions, errors in converting fractions to percentages, and misinterpreting ratios. Careful attention to detail is crucial when working with these concepts.
Conclusion: Mastering the Fundamentals
The question "What is 25 of 30?" serves as a gateway to understanding fundamental mathematical concepts that have far-reaching applications. By exploring fractions, percentages, and ratios, and by mastering the techniques of simplification and conversion, you've laid a strong foundation for tackling more complex mathematical problems. Remember, consistent practice and a firm grasp of the underlying principles are key to success in mathematics and its diverse applications in various fields. This understanding not only helps in solving problems directly but also encourages a more analytical and critical thinking approach to problem-solving in general. The more you practice, the more intuitive these concepts will become, enhancing your mathematical proficiency and opening doors to a deeper appreciation of the world around you.
Latest Posts
Latest Posts
-
Lcm Of 648 And 540
Sep 19, 2025
-
Examples Of Elements Compounds Mixtures
Sep 19, 2025
-
Who Is Ross In Macbeth
Sep 19, 2025
-
60 Degrees F To C
Sep 19, 2025
-
3 3 8 As A Fraction
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.