What Is 60 Of 21
plugunplug
Sep 23, 2025 · 5 min read
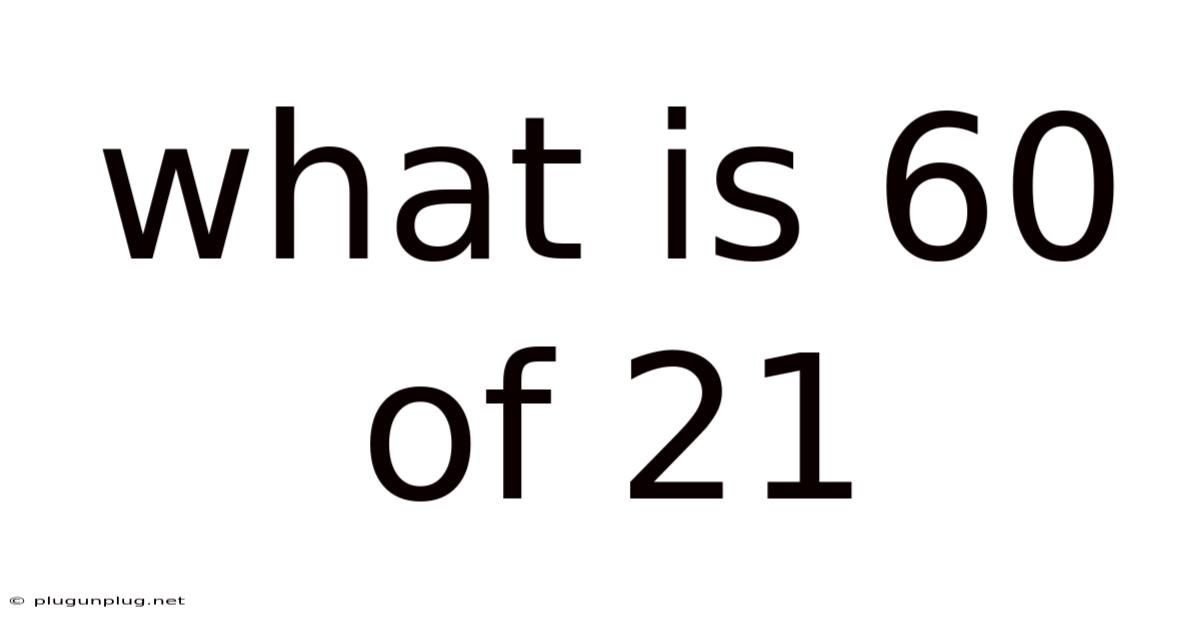
Table of Contents
What is 60% of 21? A Comprehensive Guide to Percentages and Practical Applications
Finding 60% of 21 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various aspects of life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will not only answer the question "What is 60% of 21?" but also provide a thorough explanation of percentage calculations, explore different methods for solving the problem, and delve into real-world applications of percentages.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 60% means 60 out of 100, which can be written as the fraction 60/100 or the decimal 0.60. Percentages are used extensively to represent proportions, rates, and changes in various contexts.
Method 1: Converting Percentage to Decimal
The most straightforward way to calculate 60% of 21 is to convert the percentage to its decimal equivalent and then multiply.
-
Convert the percentage to a decimal: 60% is equivalent to 60/100 = 0.60.
-
Multiply the decimal by the number: 0.60 x 21 = 12.6
Therefore, 60% of 21 is $\boxed{12.6}$.
Method 2: Using Fractions
Alternatively, we can solve this using fractions.
-
Convert the percentage to a fraction: 60% can be written as the fraction 60/100. This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 20. This simplifies to 3/5.
-
Multiply the fraction by the number: (3/5) x 21 = 63/5
-
Convert the improper fraction to a decimal: 63/5 = 12.6
Again, we arrive at the answer: 60% of 21 is $\boxed{12.6}$.
Method 3: Proportion Method
The proportion method offers a clear visual representation of the problem. We can set up a proportion:
60/100 = x/21
Where 'x' represents the unknown value (60% of 21). To solve for 'x', we cross-multiply:
100x = 60 * 21
100x = 1260
x = 1260 / 100
x = 12.6
This method confirms that 60% of 21 is $\boxed{12.6}$.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous everyday situations:
-
Shopping: Calculating discounts on sale items. If a $50 shirt is 20% off, you'll save 20% of $50, which is $10, making the final price $40.
-
Taxes: Determining the amount of sales tax or income tax owed. If the sales tax is 7%, you would calculate 7% of the purchase price to determine the tax amount.
-
Finance: Calculating interest on loans or savings accounts. Understanding interest rates is crucial for making informed financial decisions. A 5% interest rate on a $1000 loan would mean you'll pay $50 in interest per year.
-
Statistics: Analyzing data and presenting findings. Percentages are frequently used to represent proportions in surveys, polls, and scientific studies. For example, if 60% of respondents favored a particular candidate, this indicates a significant level of support.
-
Grading: Calculating grades in academic settings. If a test is worth 20% of the final grade, and you score 80%, that portion of your grade would be 16% (20% of 80%).
-
Tips: Calculating gratuity in restaurants. A common tip is 15-20% of the bill.
-
Growth and Decay: Modeling population growth, economic growth, or radioactive decay. Percentage changes are used to express the rate of increase or decrease over time.
Beyond the Basics: Advanced Percentage Concepts
While calculating 60% of 21 is relatively simple, understanding more complex percentage applications is crucial for many professions and real-life situations:
-
Percentage Increase/Decrease: These calculations measure the change in a value as a percentage of the original value. For example, if a price increases from $10 to $12, the percentage increase is 20% (($12-$10)/$10 * 100%).
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. It's a key concept in investments and loans.
-
Percentage Points: These are used to express the difference between two percentages, rather than a percentage change. For example, if unemployment falls from 10% to 8%, the decrease is 2 percentage points.
-
Weighted Averages: These involve assigning different weights to different values before calculating an average, which is particularly important in situations where certain values carry more significance. Example: Calculating your final grade in a course where different assignments have different weightings.
Frequently Asked Questions (FAQ)
Q: How can I calculate percentages quickly in my head?
A: For simple percentages like 10%, 20%, 50%, etc., you can often perform mental calculations easily. For example, 10% of a number is simply that number divided by 10. For 20%, double the result of 10%. For other percentages, it's helpful to know your basic fraction and decimal equivalents.
Q: What are some common mistakes to avoid when working with percentages?
A: Common mistakes include:
- Confusing percentage change with percentage points.
- Incorrectly calculating percentage increases or decreases.
- Using the wrong base when calculating percentages. Always identify the base value (the original number) clearly before the calculation.
- Rounding errors: Be mindful of rounding errors, especially in complex calculations.
Q: Are there any online calculators or tools that can help with percentage calculations?
A: Yes, numerous online calculators are available to help with percentage calculations. These tools can be particularly helpful for more complex problems.
Q: How can I improve my understanding of percentages?
A: Practice is key! Try solving various percentage problems, both simple and complex. You can find many practice exercises online or in textbooks. Understanding the underlying concepts – converting percentages to decimals and fractions, and the relationship between proportions – is also vital.
Conclusion
Calculating 60% of 21, which equals 12.6, is a fundamental percentage calculation. Mastering this and understanding broader percentage concepts are crucial for everyday life, academic pursuits, and professional success. By understanding the various methods for calculating percentages and being aware of common pitfalls, you can confidently tackle percentage problems across a wide range of applications. Continue practicing and exploring different scenarios to build your skills and confidence in this essential mathematical concept. Remember, consistent practice and a firm grasp of the underlying principles will make you a percentage pro in no time!
Latest Posts
Latest Posts
-
American Presidents On Mount Rushmore
Sep 23, 2025
-
Cubic Feet And Cubic Yards
Sep 23, 2025
-
Past Perfect Continuous Tense Examples
Sep 23, 2025
-
How Fast Is The Lion
Sep 23, 2025
-
120 Km H To Mph
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Of 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.