What Is 70 Of 15
plugunplug
Sep 21, 2025 · 6 min read
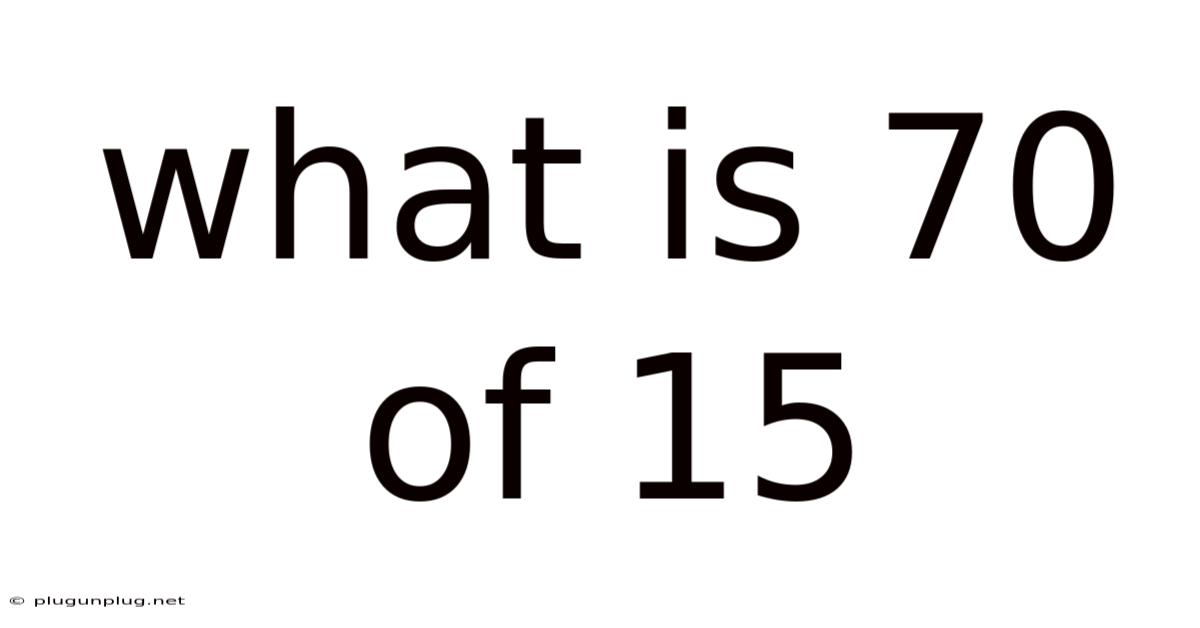
Table of Contents
What is 70% of 15? A Deep Dive into Percentages and Their Applications
Finding 70% of 15 might seem like a simple calculation, but it opens the door to understanding a fundamental mathematical concept with wide-ranging applications in everyday life, from calculating discounts to understanding statistical data. This article will not only show you how to calculate 70% of 15 but also explore the underlying principles of percentages, different methods of calculation, and real-world examples where this type of calculation is crucial.
Introduction: Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 70% means 70 out of 100, which can be written as the fraction 70/100 or the decimal 0.7. Understanding this foundational concept is key to solving percentage problems. In our case, we want to find 70% of 15, meaning we need to determine 70 parts out of 100 of the number 15.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method. We convert the percentage (70%) into its decimal equivalent (0.7) and then multiply it by the number we're interested in (15).
-
Step 1: Convert the percentage to a decimal. To do this, divide the percentage by 100. So, 70% becomes 70 ÷ 100 = 0.7.
-
Step 2: Multiply the decimal by the number. Multiply 0.7 by 15: 0.7 x 15 = 10.5
Therefore, 70% of 15 is 10.5.
Method 2: Using Fractions
This method utilizes the fractional representation of percentages. We convert the percentage into a fraction and then perform the multiplication.
-
Step 1: Convert the percentage to a fraction. 70% is equivalent to the fraction 70/100.
-
Step 2: Simplify the fraction (if possible). The fraction 70/100 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 10. This simplifies to 7/10.
-
Step 3: Multiply the fraction by the number. Multiply 7/10 by 15: (7/10) x 15 = 105/10
-
Step 4: Convert the improper fraction to a decimal. 105/10 simplifies to 10.5.
Again, we find that 70% of 15 is 10.5.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where one ratio represents the percentage (70/100) and the other represents the unknown part (x/15).
-
Step 1: Set up the proportion. We set up the proportion: 70/100 = x/15
-
Step 2: Cross-multiply. Cross-multiplying gives us: 70 * 15 = 100 * x
-
Step 3: Solve for x. This simplifies to 1050 = 100x. Dividing both sides by 100 gives us x = 10.5.
This confirms that 70% of 15 is 10.5.
Comparing the Methods
All three methods yield the same result: 10.5. The best method to use depends on personal preference and the context of the problem. The decimal method is generally the quickest, while the fraction method might be preferred if you're comfortable working with fractions. The proportion method is useful for understanding the underlying relationship between percentages and proportions.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios:
-
Discounts and Sales: Retail stores frequently offer discounts expressed as percentages. If a $15 item is on sale for 70% off, the discount amount is 10.5 (70% of 15), and the final price would be $15 - $10.5 = $4.5.
-
Taxes and Tips: Calculating sales tax or service tips involves percentages. If the sales tax is 7%, and your purchase is $15, the tax amount is 7% of $15 (which is $1.05).
-
Financial Calculations: Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating interest earned or paid requires understanding percentage calculations.
-
Statistics and Data Analysis: Percentages are widely used to represent data in charts, graphs, and reports. Understanding percentages is crucial for interpreting statistical information accurately. For example, if a survey shows that 70% of 15 respondents prefer a certain product, it means 10.5 respondents prefer it. (Note: In real-world surveys, you'd round this to the nearest whole number because you can't have a fraction of a person.)
-
Grade Calculations: In education, grades are often expressed as percentages. If a test is worth 15 points and you score 70% on it, your score would be 10.5 points.
-
Scientific Measurements: Percentages are frequently used to express quantities in science and engineering, such as percent error, percent yield in chemical reactions, or percent composition of a mixture.
Advanced Concepts and Extensions
While we've focused on calculating 70% of 15, the principles discussed can be applied to finding any percentage of any number. For instance, to find 25% of 80, you could use any of the methods described above. Additionally, you can easily adapt these methods to solve inverse percentage problems, such as determining what percentage one number is of another. For example, you might want to find what percentage 10.5 is of 15.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve percentage problems? A: Absolutely! Calculators are a convenient tool for performing these calculations quickly and accurately. Most calculators have a percentage key (%) that simplifies the process.
-
Q: What if the result is not a whole number? A: Many percentage calculations result in decimal numbers. This is perfectly acceptable, and the context will often determine whether rounding is necessary. For example, in financial calculations, you'd typically round to two decimal places to represent cents.
-
Q: How can I improve my understanding of percentages? A: Practice is key! Try solving different percentage problems using various methods to build your confidence and understanding. You can find plenty of online resources, worksheets, and practice exercises to help you.
-
Q: Are there any online tools or calculators for percentages? A: Yes, many websites and apps offer online percentage calculators that can quickly and easily compute percentage values.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 70% of 15, while seemingly a small problem, represents a gateway to mastering a vital mathematical skill. Percentages are ubiquitous in everyday life, from managing personal finances to understanding complex data. By understanding the different methods for calculating percentages – using decimals, fractions, or proportions – you equip yourself with a powerful tool for navigating the numerical world around you. This skill not only enhances your problem-solving abilities but also empowers you to make informed decisions in various aspects of your personal and professional life. Remember to practice regularly and explore the diverse applications of percentages to fully grasp their importance and utility.
Latest Posts
Latest Posts
-
3 Types Of Nuclear Radiation
Sep 21, 2025
-
Storyboard For Romeo And Juliet
Sep 21, 2025
-
Equation For F To C
Sep 21, 2025
-
Scientific Name For A Rabbit
Sep 21, 2025
-
Lcm Of 2 7 3
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.