Whats 40 Percent Of 20
plugunplug
Sep 20, 2025 · 6 min read
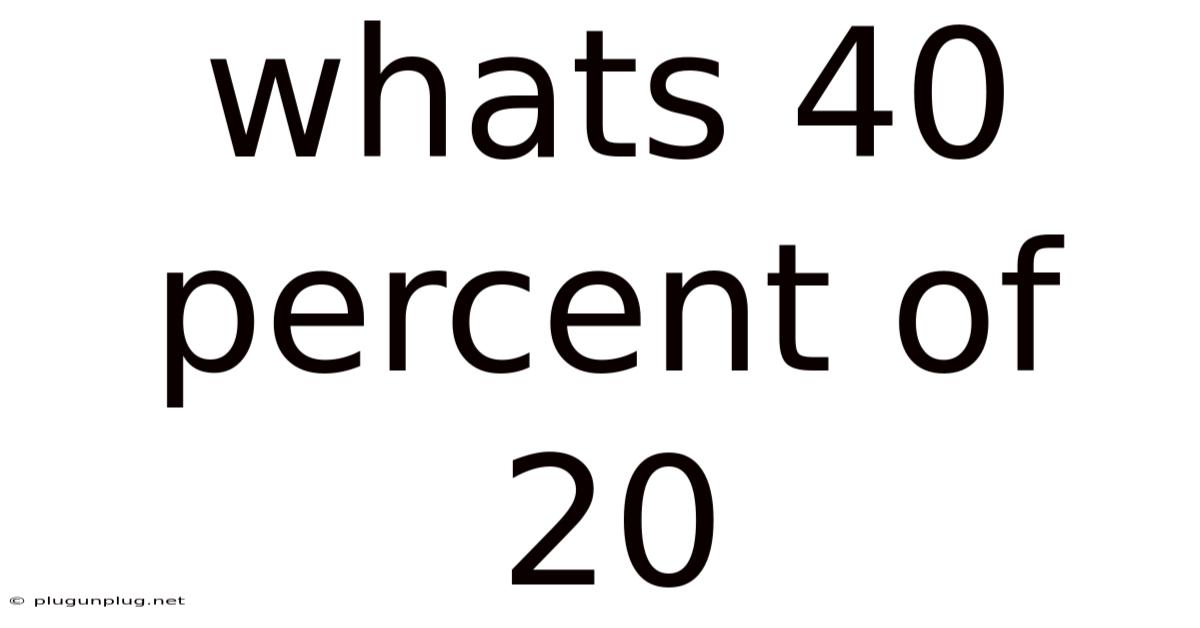
Table of Contents
What's 40 Percent of 20? A Deep Dive into Percentages and Practical Applications
Finding 40 percent of 20 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to calculate percentages and grasping the underlying concepts is crucial for various aspects of life, from managing personal finances to understanding data in professional settings. This article will not only solve this specific problem but also delve into the broader world of percentages, explaining different methods of calculation and showcasing their real-world applications. We'll explore the concept in detail, providing multiple approaches to ensure you fully understand the process and can confidently tackle similar percentage calculations in the future.
Understanding Percentages: The Basics
Before we jump into calculating 40 percent of 20, let's establish a firm understanding of what a percentage represents. The word "percent" literally means "out of one hundred." Therefore, 40 percent (often written as 40%) signifies 40 parts out of 100 equal parts of a whole. This fractional representation (40/100) is key to understanding how percentages work. We can simplify this fraction to 2/5, showing that 40% is equivalent to two-fifths of a whole.
Method 1: Using the Fraction Method
This is arguably the most intuitive method for beginners. We convert the percentage into a fraction and then multiply it by the whole number.
Steps:
-
Convert the percentage to a fraction: 40% can be written as 40/100.
-
Simplify the fraction (optional but helpful): 40/100 simplifies to 2/5.
-
Multiply the fraction by the whole number: (2/5) * 20 = 40/5 = 8
Therefore, 40 percent of 20 is 8.
Method 2: Using Decimal Conversion
This method involves converting the percentage into a decimal and then multiplying it by the whole number. This is a widely used and efficient method, especially for more complex calculations.
Steps:
-
Convert the percentage to a decimal: To convert a percentage to a decimal, divide the percentage by 100. So, 40% becomes 40 ÷ 100 = 0.40 or simply 0.4
-
Multiply the decimal by the whole number: 0.4 * 20 = 8
Again, we find that 40 percent of 20 is 8.
Method 3: Using Proportions
This method utilizes the concept of ratios and proportions, offering a more algebraic approach to solving percentage problems.
Steps:
-
Set up a proportion: We can represent the problem as a proportion: x/20 = 40/100, where 'x' represents the unknown value (40% of 20).
-
Cross-multiply: Multiply the numerator of one fraction by the denominator of the other: 100x = 40 * 20
-
Solve for x: 100x = 800. Divide both sides by 100: x = 8
Once again, we arrive at the answer: 40 percent of 20 is 8.
Understanding the Concept: Visual Representation
Imagine you have 20 apples. Finding 40% of 20 apples means finding 40 out of every 100 apples if you had 100. Since you only have 20 apples, you're finding a proportional amount. You could divide your 20 apples into five equal groups of four apples each. Two of these groups (2/5) represent 40%, totaling 8 apples. This visual representation reinforces the concept and makes it easier to grasp, especially for visual learners.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-life situations. Here are just a few examples:
-
Personal Finance: Calculating discounts, sales tax, interest rates, tips, and investment returns all involve percentage calculations. For instance, if a shirt is 20% off its original price of $50, you'll use percentage calculations to find the discount amount and the final price.
-
Business and Economics: Analyzing financial statements, calculating profit margins, understanding market share, and interpreting economic data heavily rely on percentages. For example, if a company reports a 15% increase in revenue, you need to understand percentages to comprehend the significance of this change.
-
Science and Statistics: Percentages are used extensively in scientific research and data analysis to represent proportions, probabilities, and error margins. Statistical analysis often involves calculating percentages to summarize and interpret data.
-
Everyday Life: Understanding percentages helps you make informed decisions when comparing prices, assessing deals, and understanding statistics presented in news reports or advertisements. For example, if one store offers a 10% discount and another offers a $5 discount, understanding percentages will help you choose the better deal.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a different percentage of 20?
A1: The methods described above can be applied to any percentage. Simply replace 40% with the desired percentage and follow the same steps. For example, to find 25% of 20, you would calculate (25/100) * 20 or 0.25 * 20, which equals 5.
Q2: How can I calculate percentages quickly without a calculator?
A2: For some common percentages, mental math tricks can be useful. For example, 10% is easily found by dividing the number by 10. 5% is half of 10%, and so on. Practicing mental math techniques can significantly improve your speed and efficiency in percentage calculations.
Q3: Are there any online tools or calculators to help with percentage calculations?
A3: Yes, numerous online percentage calculators are readily available. These tools can be helpful for complex calculations or when you need a quick answer. However, understanding the underlying principles is more important than relying solely on calculators.
Q4: What is the difference between percentage increase and percentage decrease?
A4: A percentage increase represents the increase in a value expressed as a percentage of the original value. A percentage decrease represents the decrease in a value expressed as a percentage of the original value. For example, if a value increases from 100 to 120, the percentage increase is 20% [(120-100)/100 * 100%]. If it decreases from 100 to 80, the percentage decrease is 20% [(100-80)/100 * 100%].
Q5: Can percentages be greater than 100%?
A5: Yes, percentages can be greater than 100%. This means the value has increased by more than its original value. For instance, if a population grows from 1000 to 1500, the percentage increase is 50%. If an investment doubles in value, it represents a 100% increase. If it triples, it's a 200% increase, and so on.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 40 percent of 20, as we've demonstrated, is a straightforward process. However, the true value lies in understanding the underlying principles of percentages and their widespread applications. From personal finance to professional endeavors, mastering percentage calculations empowers you to make informed decisions, analyze data effectively, and navigate various aspects of life with greater confidence and competence. By understanding the different methods presented here and practicing regularly, you'll not only be able to solve percentage problems but also gain a deeper appreciation for their importance in our quantitative world. Remember, the key is not just getting the right answer but also understanding why the answer is correct and how this understanding can be applied in numerous contexts.
Latest Posts
Latest Posts
-
Groups On Periodic Table Names
Sep 21, 2025
-
3 5 X 2 1
Sep 21, 2025
-
How Many Ghosts Visited Scrooge
Sep 21, 2025
-
1722 Novel By Daniel Defoe
Sep 21, 2025
-
What Irritates A Subchorionic Hematoma
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 40 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.