X 1 X 3 4
plugunplug
Sep 16, 2025 · 7 min read
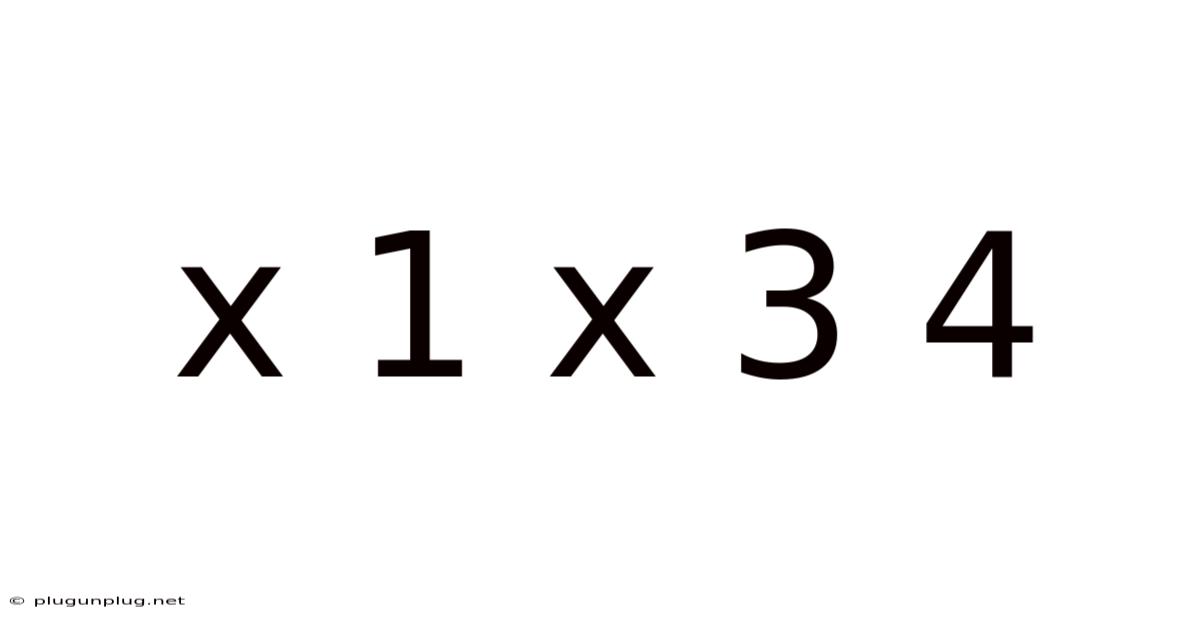
Table of Contents
Decoding the Sequence: x 1 x 3 4 – Exploring Patterns, Logic, and Problem-Solving
This article delves into the seemingly simple sequence "x 1 x 3 4," exploring various approaches to decipher its underlying pattern. We'll examine different logical methods, mathematical interpretations, and problem-solving strategies to unlock the mystery behind this sequence, ultimately aiming to predict the next number or numbers in the sequence and to understand the principles involved. This investigation will appeal to those interested in mathematics, logic puzzles, and critical thinking. We'll cover everything from basic pattern recognition to more advanced mathematical concepts, ensuring a comprehensive understanding for readers of all levels.
Understanding the Problem: Initial Observations
The sequence "x 1 x 3 4" presents a unique challenge. The presence of the unknown variable "x" immediately introduces ambiguity. Without knowing the value of "x," determining a definitive pattern is impossible. However, we can approach this problem by exploring potential interpretations and exploring possible solutions based on different assumptions about the value of "x" and the nature of the sequence itself.
Potential Interpretations and Approaches
Several approaches can be used to tackle this sequence. Let’s explore some of the most promising ones:
1. Assuming "x" is a Constant:
This approach assumes "x" represents a fixed numerical value consistent throughout the sequence. We can then explore different possible values for "x" and try to identify a pattern.
- If x = 1: The sequence becomes 1 1 1 3 4. No clear, simple pattern emerges.
- If x = 2: The sequence becomes 2 1 2 3 4. Again, no immediately apparent pattern.
- If x = 3: The sequence becomes 3 1 3 3 4. Still, no easily discernible pattern is visible.
- If x = 4: The sequence becomes 4 1 4 3 4. This also fails to reveal a straightforward pattern.
While this approach doesn't immediately yield a clear pattern, it demonstrates the importance of systematically testing different possibilities. The lack of a readily apparent pattern suggests a more complex rule might govern the sequence.
2. Exploring Arithmetic Progressions and Series:
Arithmetic progressions are sequences where the difference between consecutive terms remains constant. While the sequence doesn't appear to be a simple arithmetic progression, we can examine whether segments of the sequence could be interpreted as such. Let’s divide the sequence into smaller subsequences: (x, 1), (x, 3), (3, 4). Even analyzing these shorter sequences doesn't instantly reveal a consistent arithmetic pattern. This suggests that a more complex mathematical relationship might be at play.
3. Considering Geometric Progressions:
Geometric progressions involve sequences where the ratio between consecutive terms is constant. Applying this principle to the given sequence doesn't provide an obvious solution either. There is no readily apparent consistent ratio between consecutive numbers, even if different values of 'x' are considered.
4. Investigating Fibonacci-like Sequences:
Fibonacci sequences are characterized by the sum of two consecutive numbers producing the next number in the sequence (e.g., 1, 1, 2, 3, 5, 8...). Although our sequence doesn't directly conform to the Fibonacci sequence, we can investigate whether a modified or generalized version of the Fibonacci rule might apply. For example, could there be a hidden rule where the difference between numbers influences the generation of subsequent numbers, possibly incorporating 'x' in a unique manner? This requires further exploration and the potential introduction of additional parameters or constraints.
5. Introducing a Recursive Relationship:
A recursive relationship defines each term in the sequence based on previous terms. For example, a recursive formula could involve 'x' in a relationship with other terms. This approach allows for more flexibility in defining the sequence's generating rule. Finding such a recursive formula would require careful analysis and the establishment of a relationship between 'x' and the other known numbers in the sequence. Experimentation with various recursive formulas would be necessary to find a potential solution.
The Role of 'x' and the Limitations of Direct Solutions
The presence of 'x' introduces a significant degree of uncertainty. Without additional information or constraints, we cannot definitively solve for the next number(s) in the sequence. 'x' acts as a placeholder representing an unknown factor that significantly influences the overall structure of the sequence. Therefore, finding a definitive answer necessitates either:
- Knowing the value of 'x': If the value of 'x' were provided, the task would be significantly simplified, and we could potentially identify a clear pattern or rule.
- Discovering an inherent relationship: A pattern or relationship could exist that doesn't directly involve a simple arithmetic or geometric progression. This might require a more nuanced understanding of the sequence’s underlying logic.
- Additional constraints or context: Understanding the context in which the sequence arises—for instance, if it represents a specific mathematical problem or real-world phenomenon—might provide crucial information that allows us to determine the value of 'x' and subsequently solve the sequence.
Exploring Advanced Mathematical Concepts: Beyond Basic Patterns
If the sequence doesn't follow straightforward arithmetic or geometric progressions, more advanced concepts might be relevant. These include:
- Polynomial sequences: Polynomial sequences are defined by polynomial functions. A polynomial function could potentially model the sequence, especially if the values of 'x' were known or could be inferred.
- Generating functions: Generating functions are a powerful tool in combinatorics and number theory. They can be used to represent sequences and analyze their properties. If a generating function could be found, it could provide insights into the sequence's underlying structure.
- Difference equations: Difference equations relate terms in a sequence based on their differences. They are closely related to recurrence relations and can be used to model sequences with more complex patterns.
Problem-Solving Strategies and Critical Thinking
Solving this type of problem requires careful consideration of various problem-solving strategies:
- Systematic exploration: Trying different values for 'x' and testing various patterns is crucial. This methodical approach prevents overlooking potential solutions.
- Breaking down the problem: Dividing the sequence into smaller subsequences allows for a more focused examination of potential patterns within individual segments.
- Pattern recognition: Identifying common mathematical properties or relationships between the numbers is crucial for understanding the sequence's generation.
- Creative thinking: Moving beyond conventional mathematical patterns may be necessary. Openness to considering unconventional relationships is vital.
- Iterative refinement: Initial assumptions may require revision as new insights emerge during the problem-solving process. Flexibility and an iterative approach are essential.
Frequently Asked Questions (FAQ)
Q: Can this sequence be definitively solved without more information?
A: No, without additional information or constraints, such as the value of 'x' or the underlying mathematical context, it is impossible to definitively determine the next number(s) in the sequence. Multiple solutions could potentially exist depending on the assumptions made.
Q: What if 'x' represents a variable in an equation?
A: If 'x' represents a variable in a larger mathematical equation, the sequence might be a subset of a more comprehensive relationship. To solve this, more details about the overarching equation are needed.
Q: Are there any other potential interpretations of this sequence?
A: Yes, depending on the context, the sequence might have alternative interpretations. For example, it could represent a coded message, a sequence of events, or a pattern from a specific field of study.
Q: What mathematical concepts are relevant to solving sequences like this?
A: Several mathematical concepts can be applied, including arithmetic and geometric progressions, Fibonacci-like sequences, polynomial sequences, recursive relationships, generating functions, and difference equations.
Conclusion: The Value of Exploration and Ambiguity
The sequence "x 1 x 3 4" serves as an excellent example of a problem where ambiguity and multiple potential solutions underscore the importance of systematic exploration and critical thinking. The presence of 'x' highlights the limitations of solving a problem without sufficient information, emphasizing the need for clear problem definition and comprehensive investigation. While we cannot find a single definitive solution without additional context, exploring different approaches has demonstrated the richness and complexity of pattern recognition and mathematical problem-solving. The process of attempting to solve this seemingly simple sequence offers valuable insights into the various techniques used in tackling mathematical and logical puzzles. The exercise itself is arguably more valuable than arriving at a concrete answer, demonstrating the importance of the analytical process itself.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 1 X 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.