X 1 X 3 Integral
plugunplug
Sep 19, 2025 · 5 min read
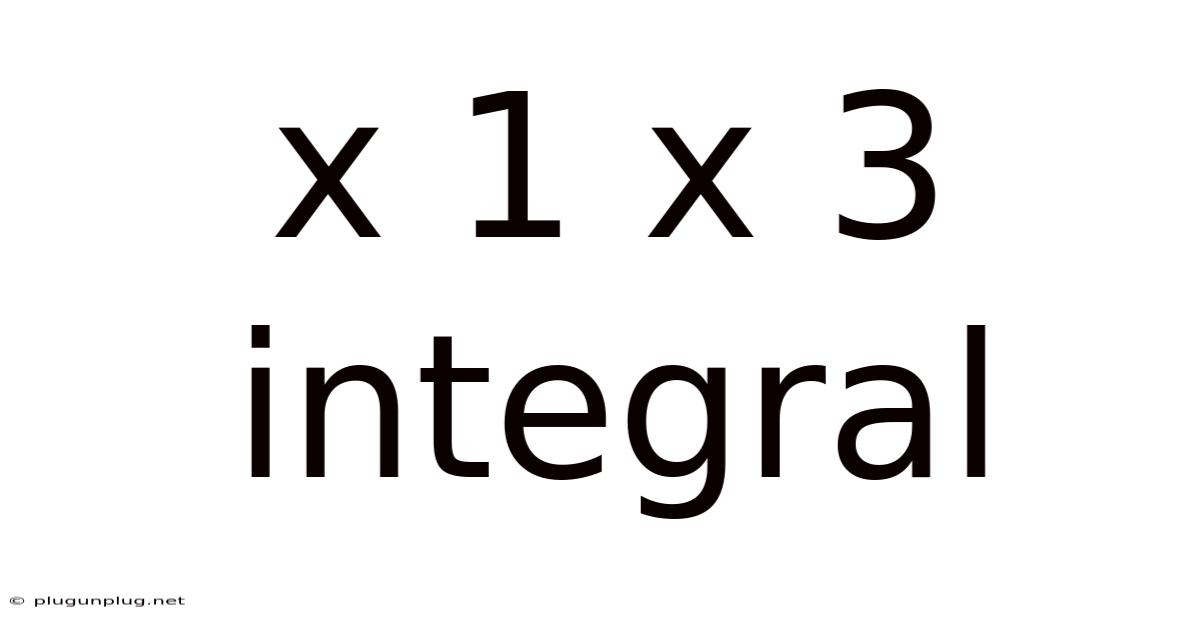
Table of Contents
Decoding the Mystery: A Comprehensive Guide to the ∫x¹ x³ dx Integral
Understanding integration is a cornerstone of calculus, and mastering various integration techniques is crucial for success in mathematics and related fields. This article delves into the seemingly simple, yet conceptually rich, definite integral ∫x¹ x³ dx, exploring its solution, the underlying principles, and common pitfalls. We will cover the process step-by-step, providing a solid foundation for tackling more complex integration problems. This guide will equip you with the knowledge and confidence to solve similar integrals and solidify your understanding of integration techniques.
Introduction: Understanding the Problem
The expression ∫x¹ x³ dx represents a definite integral. Let's break down the components:
- ∫: This symbol denotes integration, a process that finds the antiderivative of a function.
- x¹: This represents the variable x raised to the power of 1 (which is simply x). While seemingly redundant in this specific example, understanding its inclusion is vital for generalization to more complex scenarios.
- x³: This represents the variable x raised to the power of 3. This is the function we're integrating.
- dx: This signifies that the integration is with respect to the variable x.
The integral essentially asks: "What function, when differentiated, results in x¹ x³?" This might seem straightforward, but understanding the underlying algebraic manipulation and application of the power rule of integration is key.
Step-by-Step Solution: Simplifying and Integrating
Before we begin the integration process, let's simplify the integrand (the function being integrated):
x¹ x³ = x⁴
Now, our integral simplifies to:
∫x⁴ dx
This form is much easier to handle. We can now directly apply the power rule of integration.
The power rule of integration states:
∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C
where:
- n is any real number except -1
- C is the constant of integration (crucial to include because the derivative of a constant is zero).
Applying the power rule to our simplified integral:
∫x⁴ dx = (x⁴⁺¹)/(4+1) + C = (x⁵)/5 + C
Therefore, the indefinite integral of x¹ x³ dx is (x⁵)/5 + C.
The Constant of Integration: Why it Matters
The constant of integration, 'C', is an extremely important element. While often overlooked by beginners, its inclusion is vital for mathematical accuracy. Why? Because the derivative of any constant is zero. Consequently, an infinite number of functions can have the same derivative. The constant 'C' accounts for this ambiguity.
For instance, the derivative of (x⁵)/5 + 2 is the same as the derivative of (x⁵)/5 + 1000, or (x⁵)/5 + any constant. The constant of integration acknowledges this inherent uncertainty in the reverse process of differentiation.
Definite Integrals vs. Indefinite Integrals: A Crucial Distinction
The solution we arrived at, (x⁵)/5 + C, is an indefinite integral because it doesn't have defined limits of integration. A definite integral, on the other hand, has defined upper and lower limits, allowing for the calculation of a numerical value.
Let's illustrate this with an example. Suppose we want to evaluate the definite integral:
∫[from a to b] x¹ x³ dx
First, we find the indefinite integral, which we've already done: (x⁵)/5 + C
Then, we evaluate this expression at the upper limit (b) and subtract the result of evaluating it at the lower limit (a):
[(b⁵)/5 + C] - [(a⁵)/5 + C]
Notice that the constant of integration (C) cancels out. This always happens with definite integrals. Therefore, for definite integrals, you do not need to include the constant of integration in your final calculation. The result is a numerical value representing the area under the curve of x⁴ between points a and b.
Expanding the Understanding: Exploring Related Concepts
This seemingly simple integral provides a springboard to explore several crucial calculus concepts.
-
The Fundamental Theorem of Calculus: This theorem links differentiation and integration, highlighting their inverse relationship. The process of solving our integral directly demonstrates this fundamental link.
-
Area Calculation: Definite integrals provide a powerful tool for calculating areas under curves. The definite integral of x¹ x³ dx from a to b represents the area under the curve of y = x⁴ between the vertical lines x = a and x = b.
-
Applications in Physics and Engineering: Integrals are essential for solving numerous problems in physics and engineering, including calculating work, displacement, and various other physical quantities. Understanding this fundamental integral is a stepping stone towards more advanced applications.
Common Mistakes and Pitfalls
While the process seems straightforward, beginners often make these mistakes:
-
Forgetting the constant of integration (C): This is a frequent error that can significantly impact the accuracy of the result, especially in indefinite integrals.
-
Incorrect application of the power rule: Double-check your exponent calculations and ensure you're correctly adding 1 to the exponent and dividing by the new exponent.
-
Ignoring the 'dx': The 'dx' indicates the variable of integration, essential for the correct application of the power rule.
Frequently Asked Questions (FAQ)
Q: What if the exponents are different?
A: If the exponents are different, simplify the expression by multiplying the terms with the same base (x in this case) and adding their exponents before applying the power rule. For instance, ∫x² x⁵ dx simplifies to ∫x⁷ dx, which is (x⁸)/8 + C.
Q: Can this integral be solved using other methods?
A: While the power rule is the most direct and efficient method for this specific integral, more advanced techniques like substitution or integration by parts become necessary for more complex functions.
Q: What if the integral contains other terms?
A: If the integral contains multiple terms added or subtracted, integrate each term separately and then combine the results. For instance, ∫(x⁴ + 2x²) dx = (x⁵)/5 + (2x³)/3 + C.
Conclusion: Mastering the Fundamentals
The seemingly simple integral ∫x¹ x³ dx serves as a powerful illustration of fundamental integration principles. Understanding its solution, from simplifying the expression to applying the power rule and comprehending the significance of the constant of integration, is crucial for developing a robust understanding of calculus. By mastering this foundational concept, you lay a solid groundwork for tackling more challenging integrals and applying integration techniques across various mathematical and scientific domains. Remember, consistent practice and attention to detail are key to mastering integration and unlocking the power of calculus. Don't hesitate to work through numerous examples to reinforce your understanding and build your confidence. The journey to mastering calculus is iterative; each step builds upon the previous, so take your time, persevere, and celebrate your progress along the way.
Latest Posts
Latest Posts
-
What Does G H S Stand For
Sep 19, 2025
-
Quotes From Animal Farm Napoleon
Sep 19, 2025
-
Indias First Woman Prime Minister
Sep 19, 2025
-
How To Write One Million
Sep 19, 2025
-
As A Result Of Definition
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X 1 X 3 Integral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.