X 2 2x 2 0
plugunplug
Sep 16, 2025 · 6 min read
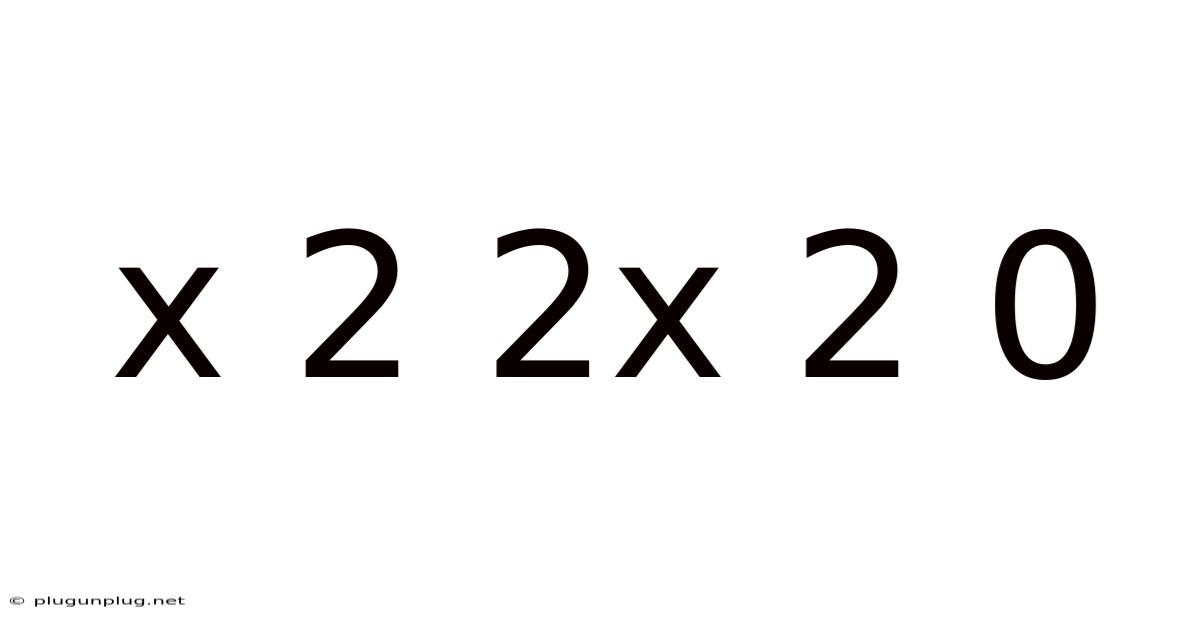
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression "x² + 2x + 2 = 0"
This article delves into the seemingly simple yet surprisingly rich mathematical expression: x² + 2x + 2 = 0. We'll explore its solution, its implications within the broader field of algebra, and its connections to more advanced mathematical concepts. Understanding this quadratic equation provides a solid foundation for grasping more complex mathematical problems. We will cover various methods of solving this equation, including the quadratic formula, completing the square, and graphical representation. Furthermore, we’ll discuss the nature of its roots and their significance.
Understanding Quadratic Equations
Before diving into the specifics of x² + 2x + 2 = 0, let's establish a foundational understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0 (if a were 0, it wouldn't be a quadratic equation).
In our specific equation, x² + 2x + 2 = 0, we have a = 1, b = 2, and c = 2. These constants determine the shape and position of the parabola represented by the equation when graphed on a Cartesian plane.
Solving the Equation: Method 1 - The Quadratic Formula
The quadratic formula is a powerful tool for solving any quadratic equation. It provides a direct method to find the values of x that satisfy the equation. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 2, c = 2), we get:
x = [-2 ± √(2² - 4 * 1 * 2)] / (2 * 1) x = [-2 ± √(4 - 8)] / 2 x = [-2 ± √(-4)] / 2
Notice that we have the square root of a negative number, √(-4). This indicates that the roots of this equation are complex numbers. Specifically, √(-4) can be simplified to 2i, where 'i' is the imaginary unit (i² = -1). Therefore, the solutions are:
x = (-2 + 2i) / 2 = -1 + i x = (-2 - 2i) / 2 = -1 - i
These are the two complex conjugate roots of the equation. This means they are of the form a ± bi, where 'a' and 'b' are real numbers. In this case, a = -1 and b = 1.
Solving the Equation: Method 2 - Completing the Square
Completing the square is another algebraic technique for solving quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's apply this method to our equation:
x² + 2x + 2 = 0
-
Move the constant term to the right side: x² + 2x = -2
-
Take half of the coefficient of x (which is 2), square it (1), and add it to both sides: x² + 2x + 1 = -2 + 1 x² + 2x + 1 = -1
-
Factor the left side as a perfect square: (x + 1)² = -1
-
Take the square root of both sides: x + 1 = ±√(-1) x + 1 = ±i
-
Solve for x: x = -1 + i x = -1 - i
This method yields the same complex conjugate roots as the quadratic formula.
Solving the Equation: Method 3 - Graphical Representation
A graphical approach provides a visual understanding of the equation's solutions. The equation x² + 2x + 2 = 0 represents a parabola. Since the parabola opens upwards (because the coefficient of x² is positive) and the discriminant (b² - 4ac = -4) is negative, the parabola does not intersect the x-axis. This confirms that the equation has no real roots, only complex roots. The vertex of the parabola can be found using the formula x = -b/2a, which gives x = -1. Substituting this back into the equation gives y = 1. Therefore, the vertex of the parabola is at (-1, 1).
A graph of the equation would show a parabola entirely above the x-axis, visually demonstrating the absence of real roots.
The Significance of Complex Roots
The fact that x² + 2x + 2 = 0 has complex roots highlights a crucial aspect of quadratic equations and algebra in general. Not all quadratic equations have real-number solutions. Complex numbers are an extension of the real number system, encompassing numbers with both real and imaginary parts. These numbers are essential in many areas of mathematics, physics, and engineering, particularly in fields involving oscillations, waves, and alternating currents.
The presence of complex conjugate roots in this specific equation isn't just a mathematical curiosity; it has implications in various applications. For example, in electrical engineering, complex numbers are used to represent impedance, and the roots of quadratic equations can represent resonant frequencies in circuits.
Further Exploration: Discriminant and Nature of Roots
The discriminant, denoted as Δ (delta), is the expression b² - 4ac within the quadratic formula. The discriminant provides valuable information about the nature of the roots of a quadratic equation:
- Δ > 0: The equation has two distinct real roots.
- Δ = 0: The equation has one real root (a repeated root).
- Δ < 0: The equation has two distinct complex conjugate roots.
In our case, Δ = -4, indicating two distinct complex conjugate roots, as we've already determined.
Applications and Connections to Other Mathematical Concepts
The concepts explored here extend far beyond this single equation. Understanding quadratic equations and their solutions is crucial for tackling more complex mathematical problems. These include:
- Higher-degree polynomial equations: Techniques used to solve quadratic equations form the basis for solving higher-degree polynomials.
- Calculus: Derivatives and integrals often involve quadratic expressions.
- Linear Algebra: Quadratic forms are fundamental in linear algebra.
- Differential Equations: Solving differential equations can sometimes lead to quadratic equations.
Frequently Asked Questions (FAQs)
Q: What are complex numbers?
A: Complex numbers are numbers of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (i² = -1). 'a' is the real part, and 'b' is the imaginary part.
Q: Why are complex roots important?
A: Complex roots are essential in many areas of science and engineering, providing solutions to problems that wouldn't have solutions within the realm of real numbers alone. They are especially crucial in fields involving oscillations and waves.
Q: Can a quadratic equation have only one root?
A: Yes, a quadratic equation can have only one real root, which occurs when the discriminant (b² - 4ac) is equal to zero. This root is often referred to as a repeated root.
Q: Is there a way to visualize complex roots?
A: While not as intuitive as visualizing real roots on a number line, complex roots can be represented on a complex plane (also known as an Argand diagram), where the real part is plotted on the horizontal axis and the imaginary part on the vertical axis.
Conclusion
The seemingly simple equation x² + 2x + 2 = 0 provides a rich and insightful journey into the world of quadratic equations and complex numbers. Through the exploration of various solution methods and the analysis of its roots, we've highlighted the importance of complex numbers and their wide-ranging applications. This understanding serves as a robust foundation for further exploration of more advanced mathematical concepts. Remember, the seemingly simple often holds hidden depths of mathematical beauty and utility. Continue exploring, questioning, and expanding your mathematical horizons!
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 2x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.