X 2 X 3 6
plugunplug
Sep 23, 2025 · 6 min read
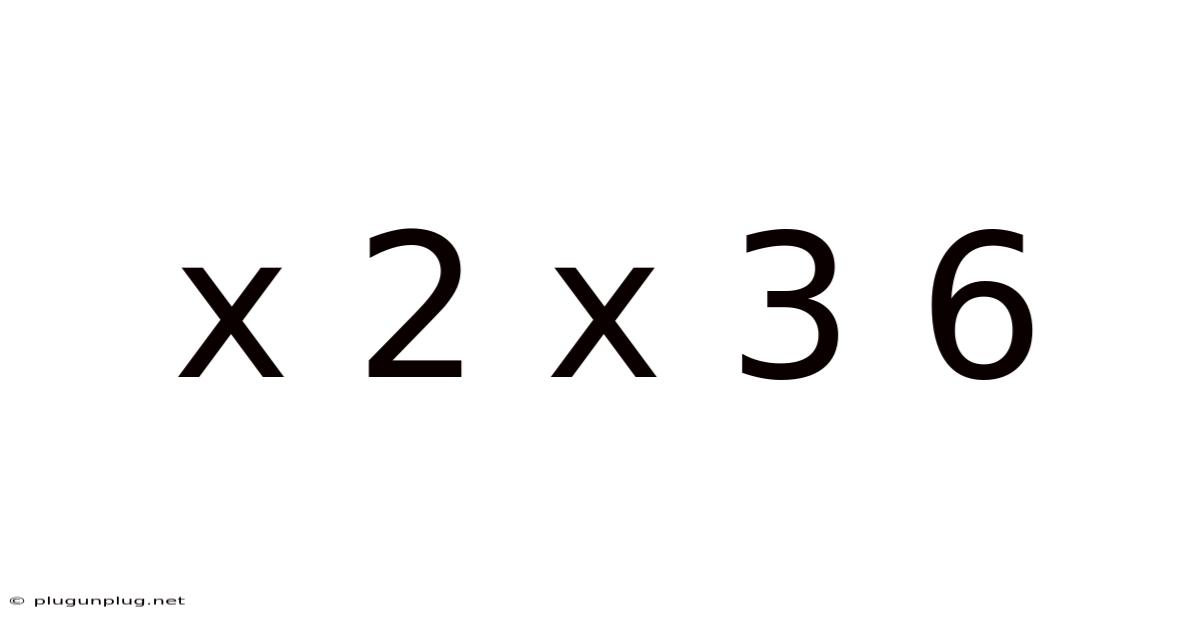
Table of Contents
Decoding the Seemingly Simple: Exploring the Mathematical World Behind 2 x 3 = 6
The seemingly simple equation, 2 x 3 = 6, acts as a gateway to a vast and fascinating world of mathematics. While the answer might seem obvious to even the youngest learners, understanding the underlying principles and exploring its broader implications reveals a depth far beyond the immediate calculation. This article delves into the multifaceted nature of this fundamental equation, exploring its historical context, different interpretations, and its relevance across numerous mathematical concepts. We will unravel its meaning from the basic principles of multiplication to its advanced applications in algebra, calculus, and beyond.
I. Introduction: Multiplication – The Foundation of 2 x 3 = 6
At its core, 2 x 3 = 6 represents a multiplication problem. Multiplication, a fundamental arithmetic operation, is essentially repeated addition. In this case, 2 x 3 means adding the number 2 three times: 2 + 2 + 2 = 6. This simple interpretation forms the basis for understanding more complex mathematical concepts. Understanding this fundamental concept is crucial for grasping higher-level mathematics, from fractions and decimals to algebra and calculus. This seemingly simple equation lays the groundwork for much more intricate mathematical ideas.
II. Visualizing 2 x 3 = 6: A Concrete Approach
For young learners, visual aids are crucial for solidifying their understanding of multiplication. Numerous methods can effectively demonstrate 2 x 3 = 6:
-
Arrays: Imagine arranging two rows of three objects each (e.g., apples, blocks, or counters). Counting all the objects provides a tangible representation of the result: six. This visual method helps connect the abstract concept of multiplication to a concrete reality.
-
Number Lines: Jumping three steps, two times, along a number line, starting at zero, will lead to six. This method helps visualize repeated addition.
-
Area Models: A rectangle with a length of 3 units and a width of 2 units has an area of 6 square units. This illustrates multiplication as finding the area of a rectangle, a concept extensively used in geometry and beyond.
These visual representations make the abstract concept of multiplication more accessible and understandable for learners of all ages.
III. The Commutative Property: The Order Doesn't Matter
A key property of multiplication is its commutativity. This means that the order of the numbers being multiplied doesn't affect the result. In our example, 2 x 3 is equal to 3 x 2. Both expressions result in 6. This seemingly simple fact has significant implications in simplifying calculations and understanding more complex mathematical structures. The commutative property is not only crucial in arithmetic but also extends to more advanced areas like matrix multiplication, where the order of operations significantly influences the outcome. However, it is crucial to remember that this property is not applicable to all mathematical operations. For instance, subtraction and division are not commutative.
IV. Beyond the Basics: Expanding the Scope of 2 x 3 = 6
While 2 x 3 = 6 is a simple equation, its implications extend far beyond basic arithmetic. Let's explore some of these connections:
-
Fractions and Decimals: The equation can be extended to include fractions and decimals. For example, (2/1) x (3/1) = 6/1 = 6, showing the connection between whole numbers and fractions. Similarly, 2.0 x 3.0 = 6.0, illustrating the application of multiplication with decimals.
-
Algebra: In algebra, 2x = 6 is an equation where 'x' represents an unknown variable. Solving for 'x' involves dividing both sides of the equation by 2, leading to x = 3. This demonstrates how simple multiplication is fundamental to solving algebraic equations. More complex algebraic expressions and equations are built upon this basic foundation.
-
Geometry: As mentioned earlier, the area of a rectangle with sides of length 2 and 3 units is 6 square units. This connection between multiplication and geometry extends to calculating volumes of three-dimensional shapes and other geometric concepts. Understanding this relationship is crucial in fields like engineering and architecture.
-
Calculus: Though seemingly distant, the concept of multiplication underlies fundamental calculus concepts. For instance, the derivative of a function involves finding the instantaneous rate of change, which often involves limiting processes based on multiplication and division. The foundation laid by simple equations like 2 x 3 = 6 is essential in grasping these more advanced mathematical concepts.
V. Exploring Different Number Systems: Beyond Base 10
Our familiar decimal system (base 10) is just one way to represent numbers. Let's consider how 2 x 3 = 6 translates to other number systems:
-
Binary (Base 2): In binary, 2 is represented as 10 and 3 as 11. Multiplying 10 (2) and 11 (3) in binary yields 110, which translates back to 6 in base 10. This illustrates how the fundamental concept of multiplication remains consistent across different number systems.
-
Hexadecimal (Base 16): Similar to binary, the principles of multiplication remain consistent. Understanding how numbers are represented and manipulated in different bases is crucial in computer science and other fields dealing with digital systems.
VI. Applications in Real-World Scenarios: The Practicality of 2 x 3 = 6
The seemingly simple equation, 2 x 3 = 6, has countless real-world applications:
-
Everyday Calculations: From calculating the total cost of two items costing $3 each to determining the number of cookies in two bags with three cookies each, multiplication is used extensively in daily life.
-
Business and Finance: In business, calculating profits, costs, and determining pricing often involves multiplication.
-
Science and Engineering: In scientific and engineering applications, multiplication is used extensively in calculations related to physics, chemistry, and engineering design.
VII. The Historical Context: A Journey Through Time
The concept of multiplication has ancient roots, evolving over centuries. Early civilizations developed various methods for multiplication, often using visual aids or physical objects. The development of sophisticated mathematical systems and the use of algorithms for multiplication is a testament to human ingenuity and the enduring significance of this fundamental operation. Understanding the historical context of multiplication provides a broader perspective on the significance of simple equations like 2 x 3 = 6.
VIII. Frequently Asked Questions (FAQ)
-
Q: Is multiplication always commutative? A: Yes, multiplication of real numbers is always commutative. However, this is not true for all mathematical operations or in all mathematical structures (e.g., matrix multiplication).
-
Q: What is the inverse operation of multiplication? A: Division is the inverse operation of multiplication.
-
Q: How does multiplication relate to other mathematical operations? A: Multiplication is closely related to addition (repeated addition), subtraction (repeated subtraction can be viewed as related to multiplication with negative numbers), and division (the inverse operation).
IX. Conclusion: A Foundation for Mathematical Understanding
The equation 2 x 3 = 6, while seemingly simple, provides a profound entry point into the world of mathematics. Its exploration reveals the interconnectedness of various mathematical concepts, from basic arithmetic to advanced algebra and calculus. Understanding its underlying principles and visual representations is essential for building a solid foundation in mathematics, crucial for success in numerous academic and professional fields. The simplicity of this equation belies its immense power and far-reaching implications, highlighting the beauty and elegance of mathematical principles. From its historical context to its real-world applications, 2 x 3 = 6 showcases the fundamental importance of mathematics in our world. It is not just an equation; it is a gateway to understanding the intricate and fascinating world of numbers.
Latest Posts
Latest Posts
-
Convert 75 Cm To Inches
Sep 23, 2025
-
Convert Km To Miles Formula
Sep 23, 2025
-
Is 25 A Square Number
Sep 23, 2025
-
Meaning Of Balance Brought Forward
Sep 23, 2025
-
What Did The Raven Say
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.