X 2 X 3 X
plugunplug
Sep 16, 2025 · 6 min read
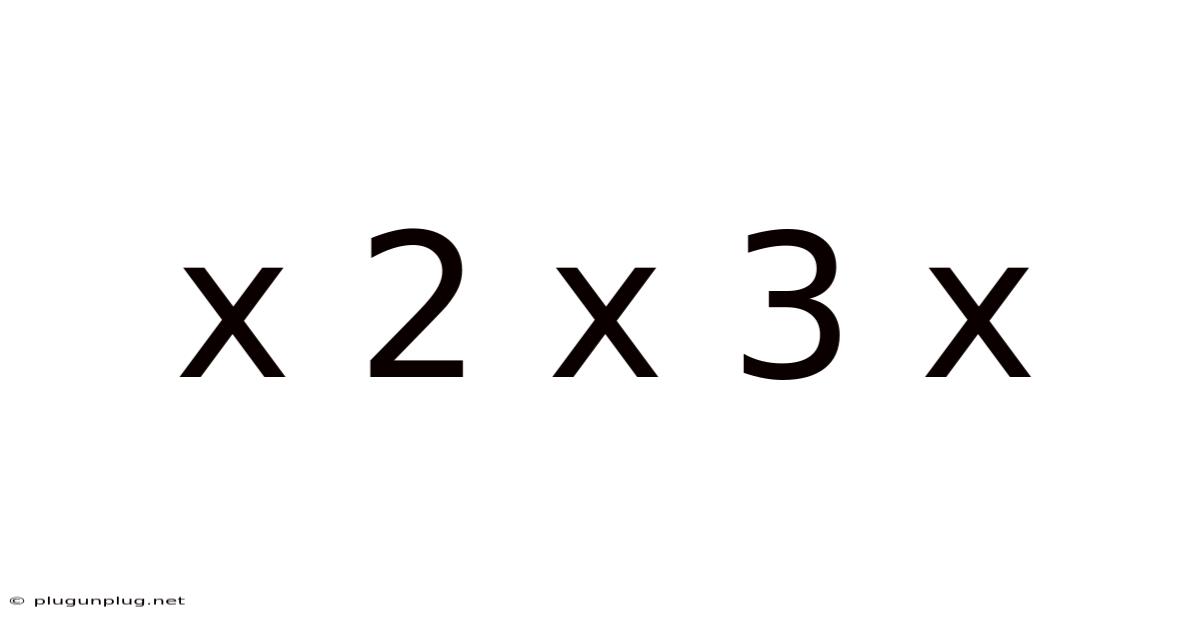
Table of Contents
Decoding the Mystery: Exploring the Mathematical Expression "x 2 x 3 x"
This article delves into the seemingly simple yet surprisingly complex mathematical expression "x 2 x 3 x". While at first glance it might seem like a straightforward calculation, the lack of explicit operators introduces ambiguity and opens up a world of possibilities depending on the interpretation. We will explore various interpretations, discuss the order of operations, and examine the different results that can be obtained. We'll also touch upon the importance of clear mathematical notation and how seemingly small details can significantly impact the outcome. Understanding this expression helps us build a stronger foundation in mathematical reasoning and problem-solving.
Understanding the Ambiguity: The Role of Operators
The expression "x 2 x 3 x" is inherently ambiguous because it lacks clearly defined operators between the variables and numbers. In mathematics, operators like '+', '-', '*', and '/' dictate the actions to be performed. The absence of these symbols forces us to consider different possibilities based on assumed operations. This ambiguity highlights the crucial role of precise mathematical notation in avoiding confusion and ensuring accurate calculations.
Interpretation 1: Implicit Multiplication
One common interpretation is to assume implicit multiplication between all elements. This means we treat the expression as if it were written: x * 2 * x * 3 * x. In this case, we can simplify the expression using the commutative and associative properties of multiplication:
x * 2 * x * 3 * x = 2 * 3 * x * x * x = 6x³
This interpretation yields a simple polynomial expression, 6x³, where the result depends on the value of 'x'. If, for example, x = 2, then the expression evaluates to 6 * (2³) = 6 * 8 = 48.
Interpretation 2: Mixed Operations – Considering Addition
Let's explore a scenario where we assume a mix of multiplication and addition. One possible interpretation could be: (x + 2) * (x + 3) * x. This introduces a more complex expression, requiring us to expand the brackets using the distributive property (often referred to as the FOIL method for binomials):
(x + 2) * (x + 3) * x = (x² + 3x + 2x + 6) * x = (x² + 5x + 6) * x = x³ + 5x² + 6x
This interpretation results in a cubic polynomial, x³ + 5x² + 6x. The outcome, unlike the previous interpretation, is significantly different and depends heavily on the value assigned to 'x'. For instance, if x = 2, the result would be 2³ + 5(2²) + 6(2) = 8 + 20 + 12 = 40.
Interpretation 3: Exploring Other Operational Combinations
The possibilities don't end there. We could explore various other combinations of addition, subtraction, and multiplication, each leading to a unique result. For instance:
- x + 2 * x + 3 * x: Following the order of operations (PEMDAS/BODMAS), we would first perform the multiplications: x + 2x + 3x = 6x. This is a linear expression.
- x * 2 + x * 3 + x: Again, multiplication first: 2x + 3x + x = 6x. This also results in a linear expression.
- x * (2 + x) * 3 * x: This would be: 3x(2x + x²) = 6x² + 3x³.
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), is crucial in evaluating mathematical expressions. These rules dictate the sequence in which operations should be performed. Without clear operators and parentheses, the order of operations becomes ambiguous, leading to different interpretations and potentially incorrect results. The expressions explored above demonstrate how different interpretations based on assumed order of operations can yield vastly different outcomes.
Beyond Simple Interpretations: Functional Analysis
The expression "x 2 x 3 x" can also be viewed from a more advanced perspective, such as through the lens of functional analysis. If we consider 'x' as a variable representing an input to a function, then the expression could represent a composite function where the output of one function becomes the input of another. The specific functions would depend on the assumed operations between the components. This interpretation introduces the concepts of function composition and domain and range considerations.
Practical Applications and Real-World Examples
While the expression itself might seem abstract, the principles illustrated – ambiguity in notation, the importance of order of operations, and the different interpretations leading to varied results – have practical implications in various fields:
- Computer programming: In programming, the order of operations is strictly defined. Ambiguous expressions can lead to errors and unexpected program behavior. Programmers must pay close attention to operator precedence and use parentheses to clarify the intended order of operations.
- Engineering and physics: Formulas in engineering and physics often involve complex expressions. Clear notation and a thorough understanding of order of operations are essential to ensure accurate calculations and reliable results. Ambiguity can lead to design flaws and potentially dangerous consequences.
- Data analysis: In data analysis and statistical modeling, interpreting formulas and expressions correctly is crucial for drawing accurate conclusions from data. Ambiguity in formulas can lead to misinterpretations and incorrect analyses.
Frequently Asked Questions (FAQ)
Q: What is the single "correct" answer to x 2 x 3 x?
A: There is no single "correct" answer without further specification of the intended operations. The expression is inherently ambiguous and requires clarifying the operators (+, -, *, /) and possibly using parentheses to establish the correct order of operations.
Q: Why is clear mathematical notation so important?
A: Clear mathematical notation is essential to avoid ambiguity and ensure accurate calculations. Ambiguous expressions can lead to misunderstandings, errors, and potentially incorrect conclusions. Using parentheses and clearly stating operators prevents misinterpretations.
Q: How can I avoid ambiguity in my own mathematical expressions?
A: Use parentheses liberally to group operations and specify the order in which they should be performed. Clearly state all operators (+, -, *, /) to leave no room for interpretation. Avoid relying on implicit multiplication or other implied operations whenever possible.
Q: Can this expression be simplified further if we know the value of 'x'?
A: Yes, once you assign a value to 'x' and decide on an interpretation (a specific order of operations), the expression can be evaluated to a single numerical value. However, the process of simplification will depend heavily on the interpretation chosen.
Conclusion: The Power of Precision in Mathematics
The seemingly simple expression "x 2 x 3 x" serves as a powerful reminder of the importance of precision and clarity in mathematical notation. The ambiguity inherent in this expression highlights the critical role of explicitly defining operators and using parentheses to ensure accurate calculations. By exploring different interpretations and understanding the principles of order of operations, we gain a deeper appreciation for the nuances of mathematical expression and the potential consequences of ambiguity. This exercise reinforces the fundamental principles of mathematical reasoning and problem-solving, valuable skills applicable across various fields. The lack of explicit operators in the original expression leads to several valid solutions, depending on the interpretation. Therefore, precise mathematical writing is crucial for unambiguous communication and accurate results.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 X 3 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.