X 2 Y 2 3
plugunplug
Sep 16, 2025 · 6 min read
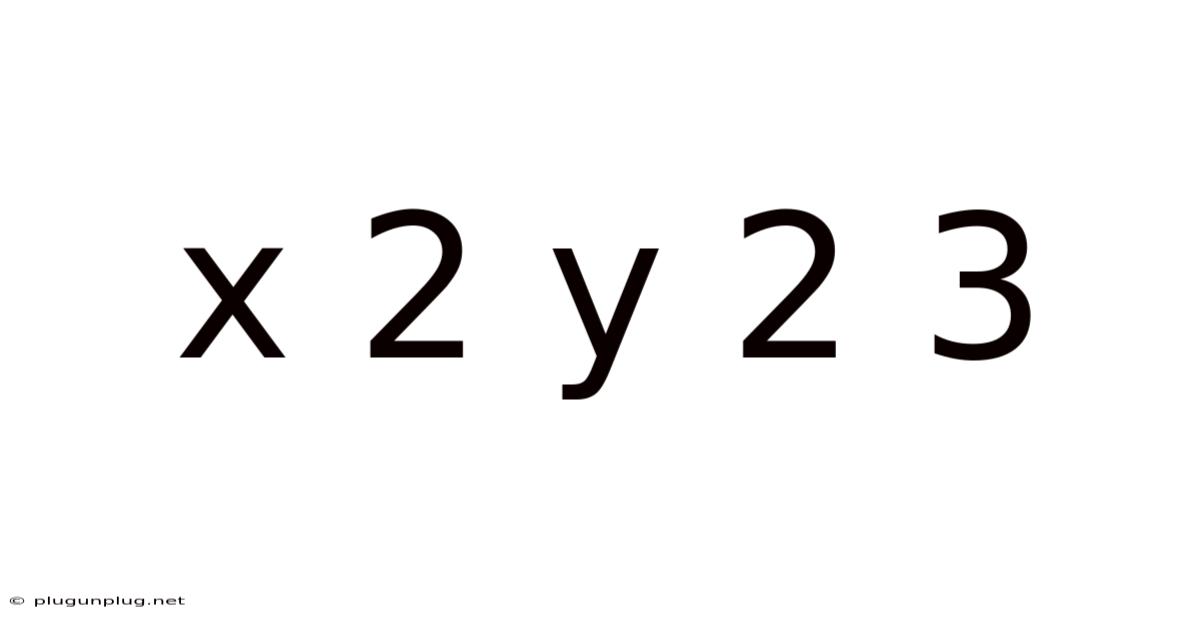
Table of Contents
Decoding the Enigma: A Deep Dive into x² + y² = 3
The equation x² + y² = 3 might seem deceptively simple at first glance. This seemingly straightforward algebraic expression, however, opens a door to a fascinating world of mathematical concepts, encompassing geometry, number theory, and even abstract algebra. This article will explore this equation in detail, examining its geometric representation, analyzing its solutions, and delving into its implications within various mathematical branches. We'll unpack its complexities, making it accessible to a wide range of readers, from high school students to those with a stronger mathematical background.
Understanding the Geometric Interpretation
Before diving into the algebraic solutions, let's visualize the equation geometrically. In a Cartesian coordinate system, x² + y² = 3 represents a circle centered at the origin (0,0) with a radius of √3. This is because the equation is a direct application of the Pythagorean theorem: x² + y² represents the square of the distance from any point (x, y) to the origin, and 3 is the square of the radius. This geometric representation immediately provides valuable insights into the nature of the solutions.
Finding the Solutions: A Numerical Approach
Solving x² + y² = 3 means finding all pairs of real numbers (x, y) that satisfy the equation. While there's no single, straightforward algebraic manipulation to find all solutions, we can explore several approaches:
-
Direct Substitution: We can choose a value for x and solve for y (or vice versa). For instance, if x = 0, then y² = 3, leading to y = ±√3. Similarly, if y = 0, then x = ±√3. This gives us four immediate solutions: (0, √3), (0, -√3), (√3, 0), and (-√3, 0).
-
Iterative Methods: For more complex scenarios or to find approximate solutions, iterative methods like the Newton-Raphson method can be employed. These methods refine an initial guess to find increasingly accurate solutions. However, due to the nature of the equation, an analytical solution is more readily available.
-
Parametric Representation: A powerful technique is to use parametric equations. We can express x and y in terms of a parameter, typically an angle θ. Using trigonometric functions, we can write:
- x = √3 * cos(θ)
- y = √3 * sin(θ)
As θ varies from 0 to 2π, (x, y) traces the entire circle, providing all possible solutions.
Exploring the Solutions: Rational and Irrational Numbers
The solutions to x² + y² = 3 reveal an interesting interplay between rational and irrational numbers. While the solutions we found directly (e.g., (√3, 0)) involve irrational numbers (√3 is irrational), the equation also allows for solutions involving both rational and irrational numbers. It's crucial to understand that not all solutions are easily expressed; many involve irrational numbers. The density of these points on the circumference of the circle is infinite, a testament to the richness of the real number system.
Connections to Number Theory: Pythagorean Triples and Beyond
The equation x² + y² = 3 has direct connections to number theory, particularly regarding Pythagorean triples. A Pythagorean triple (a, b, c) is a set of three positive integers satisfying a² + b² = c². Our equation, however, doesn't directly lead to integer solutions because 3 isn't the square of an integer. However, exploring variations of the equation, such as finding integer solutions to x² + y² = n for different values of n, opens up a world of exploration into Diophantine equations (equations where only integer solutions are sought). The study of these equations is a rich area within number theory.
Complex Numbers: Expanding the Solution Set
Expanding our scope to include complex numbers significantly broadens the solution set. If we allow x and y to be complex numbers (of the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit), the equation x² + y² = 3 admits a much larger number of solutions. This realm leads us into the fascinating world of complex analysis and the geometric interpretation of complex numbers in the complex plane.
Applications in Physics and Engineering
While this equation might not be explicitly used in many everyday physics or engineering problems, the underlying principles – the geometry of circles, the manipulation of quadratic equations, and the use of trigonometric functions – are fundamental to many applications. The equation’s representation of a circle is directly applicable in various fields involving circular motion, wave propagation, and vector analysis.
Further Explorations and Related Concepts
The exploration of x² + y² = 3 opens doors to several related mathematical concepts that are worth exploring:
-
Higher-Dimensional Analogues: The concept can be extended to higher dimensions. In three dimensions, for example, we could consider x² + y² + z² = 3, representing a sphere.
-
Elliptic Curves: Elliptic curves are equations of the form y² = x³ + ax + b, which have far-reaching applications in cryptography and number theory. While seemingly different, the underlying principles of solving nonlinear equations and their geometric representation share similarities.
-
Diophantine Equations: As mentioned earlier, finding integer solutions to equations like x² + y² = n is a significant area of study in number theory, with deep connections to advanced concepts.
Frequently Asked Questions (FAQ)
Q: Are there any integer solutions to x² + y² = 3?
A: No, there are no integer solutions. The squares of integers are always non-negative, and the only integer squares less than or equal to 3 are 0 and 1. No combination of 0 and 1 can add up to 3.
Q: Can this equation be solved using only algebra?
A: While we can find some specific solutions through algebraic manipulation (like setting x=0 or y=0), finding all solutions using pure algebra is not straightforward. Parametric representation, using trigonometry, provides a complete solution set.
Q: What software or tools can be used to visualize the equation?
A: Many tools can visualize this equation, including graphing calculators (like those from TI or Casio), mathematical software like MATLAB or Mathematica, and even online graphing tools. Simply input the equation to see the circle represented graphically.
Q: What is the significance of the number 3 in this equation?
A: The number 3 determines the radius of the circle (√3). Changing this value would change the size of the circle but maintain its central position at the origin.
Conclusion
The seemingly simple equation x² + y² = 3 offers a profound exploration into various mathematical fields. From its geometric representation as a circle to its intricate connection with number theory and complex numbers, this equation serves as a microcosm of mathematical richness. By understanding its solutions and the techniques used to find them, we gain a deeper appreciation for the beauty and power of mathematics, revealing a world far beyond its initial simplicity. Further exploration into related topics will undoubtedly enrich one's mathematical understanding and open avenues for further intellectual inquiry.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 Y 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.