2 Out Of 14 Percentage
plugunplug
Sep 24, 2025 · 6 min read
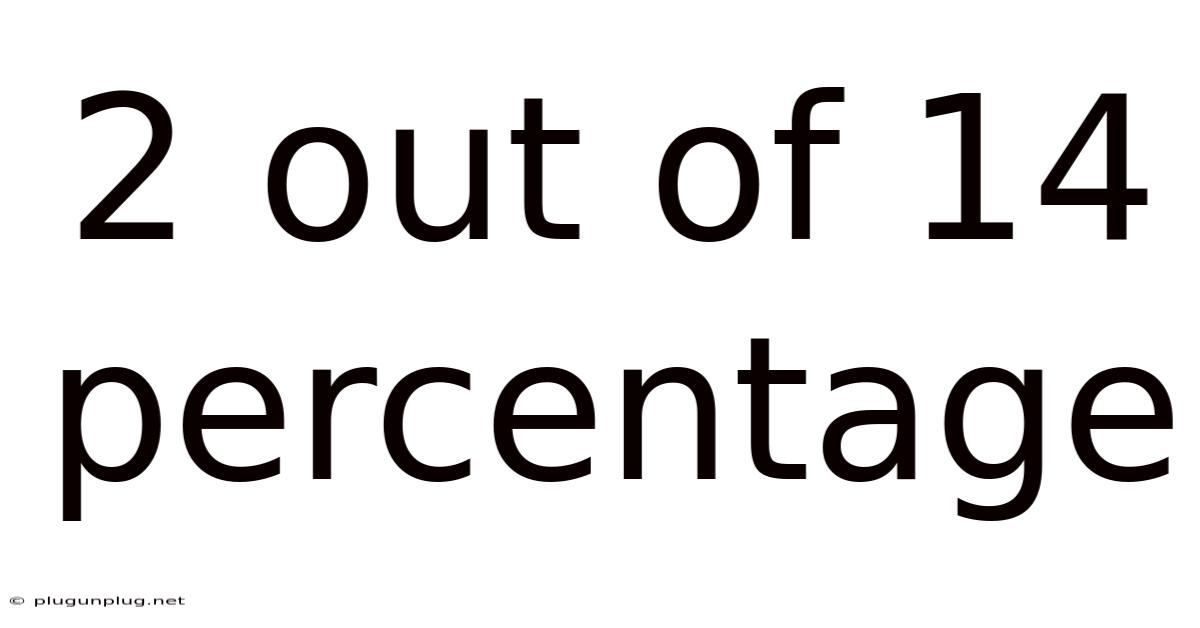
Table of Contents
Decoding 2 out of 14: Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. This article delves into the meaning of "2 out of 14," explains how to calculate this as a percentage, and explores various applications and interpretations. We'll also tackle common misconceptions and provide practical examples to solidify your understanding. Learning to calculate and interpret percentages empowers you to make informed decisions in various aspects of life.
Understanding the Basics: Fractions, Decimals, and Percentages
Before we dive into calculating "2 out of 14" as a percentage, let's refresh the relationship between fractions, decimals, and percentages. These three represent the same value, just expressed differently:
-
Fraction: A fraction represents a part of a whole. In our case, "2 out of 14" is represented as the fraction 2/14.
-
Decimal: A decimal represents a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000). To convert a fraction to a decimal, divide the numerator by the denominator.
-
Percentage: A percentage represents a fraction where the denominator is 100. It indicates "per hundred" or "out of 100." The symbol "%" is used to represent percentage.
Calculating 2 out of 14 as a Percentage: A Step-by-Step Guide
Here's how to calculate "2 out of 14" as a percentage:
Step 1: Express it as a fraction:
The phrase "2 out of 14" translates directly to the fraction 2/14.
Step 2: Simplify the fraction (optional but recommended):
We can simplify 2/14 by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This simplifies the fraction to 1/7. Simplifying makes the subsequent calculations easier.
Step 3: Convert the fraction to a decimal:
Divide the numerator (1) by the denominator (7): 1 ÷ 7 ≈ 0.142857
Step 4: Convert the decimal to a percentage:
Multiply the decimal by 100 and add the "%" symbol: 0.142857 × 100 ≈ 14.29%
Therefore, 2 out of 14 is approximately 14.29%.
Interpreting the Result: What Does 14.29% Mean?
The result, 14.29%, means that 2 represents approximately 14.29% of the total of 14. In other words, if you had 14 items and 2 of them possessed a specific characteristic, those 2 items would constitute roughly 14.29% of the total.
Practical Applications of Percentage Calculations
Percentage calculations are incredibly versatile and are used in a wide range of scenarios:
-
Business and Finance: Calculating profit margins, interest rates, discounts, sales tax, and investment returns all rely heavily on percentage calculations. For example, if a company's revenue increases by 10%, this represents significant growth.
-
Science and Statistics: Percentages are used to represent data in scientific studies, surveys, and statistical analyses. For example, researchers might report that 60% of participants in a study showed a positive response to a treatment.
-
Everyday Life: Percentages help us understand discounts in stores ("20% off!"), calculate tips in restaurants, or determine the nutritional content of food ("5% fat").
-
Education: Grade calculations, test scores, and class participation often involve percentages. A score of 85% on an exam indicates a good understanding of the material.
-
Health and Medicine: Percentage changes in weight, blood pressure, or other health indicators are crucial for monitoring health conditions. For instance, a 10% increase in blood pressure can be a cause for concern.
Common Misconceptions about Percentages
Several common misconceptions surround percentages:
-
Adding Percentages Incorrectly: It's incorrect to simply add percentages without considering the base value. For instance, a 10% increase followed by a 10% decrease does not result in the original value; it will result in a slightly lower value.
-
Misinterpreting Percentage Change: A percentage increase or decrease always refers to the change relative to the original value, not the new value. A 50% increase from 100 is 150, but a 50% decrease from 150 is not back to 100.
-
Ignoring Sample Size: When interpreting percentages from surveys or polls, it's crucial to consider the sample size. A percentage might seem significant, but if based on a small sample, it may not accurately represent the larger population.
Expanding on the 2 out of 14 Example: Real-World Scenarios
Let's imagine a few scenarios where the "2 out of 14" calculation might apply:
-
Quality Control: A factory produces 14 widgets, and 2 are defective. The defect rate is 14.29%. This information is crucial for identifying and addressing quality control issues.
-
Survey Results: In a survey of 14 respondents, 2 preferred a particular product. The preference rate for that product is 14.29%. This insight helps the company understand consumer preferences.
-
Classroom Performance: Out of 14 students in a class, 2 failed a test. The failure rate is 14.29%. This highlights the need for additional support or adjustments to teaching methods.
Beyond Simple Percentages: More Complex Applications
While calculating "2 out of 14" provides a basic understanding, percentages often appear in more complex scenarios:
-
Compound Interest: Calculating compound interest involves repeated percentage calculations over time. Understanding compound interest is vital for financial planning and investment decisions.
-
Statistical Significance: In statistical testing, percentages are used to determine the significance of results. A p-value (probability value) represents the probability that observed results occurred by chance.
-
Growth Rates: Businesses track growth rates (e.g., revenue growth, market share growth) using percentages. This allows for comparisons over time and against competitors.
Frequently Asked Questions (FAQ)
Q: How can I calculate percentages quickly in my head?
A: For simple percentages like 10%, 25%, or 50%, you can perform mental calculations. For example, 10% is simply dividing by 10, and 50% is dividing by 2. For other percentages, estimations are often sufficient.
Q: What if I have a percentage and need to find the original value?
A: You can use reverse percentage calculations. For example, if an item is discounted by 20% and costs $80, the original price can be calculated as $100.
Q: Are there online tools or calculators for percentage calculations?
A: Yes, numerous online calculators are readily available for various percentage-related calculations, from simple conversions to more complex scenarios.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is not merely an academic exercise; it's a practical life skill. From managing personal finances to interpreting data in professional settings, the ability to calculate and interpret percentages empowers informed decision-making. This article aimed to demystify the process, illustrate real-world applications, and highlight common misconceptions. By mastering this fundamental concept, you equip yourself with a powerful tool for navigating the complexities of the modern world. Remember that while this article focused on the specific calculation of "2 out of 14," the principles and techniques discussed apply broadly to various percentage calculations you will encounter. Practice makes perfect, so apply these techniques in different contexts to solidify your understanding.
Latest Posts
Latest Posts
-
What Is 19c In Fahrenheit
Sep 24, 2025
-
5 9 Divided By 5
Sep 24, 2025
-
Whats 5 Percent Of 2000
Sep 24, 2025
-
7 Tbsp Butter In Grams
Sep 24, 2025
-
What Is Numerator And Denominator
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2 Out Of 14 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.