2 X 2 X 12
plugunplug
Sep 22, 2025 · 6 min read
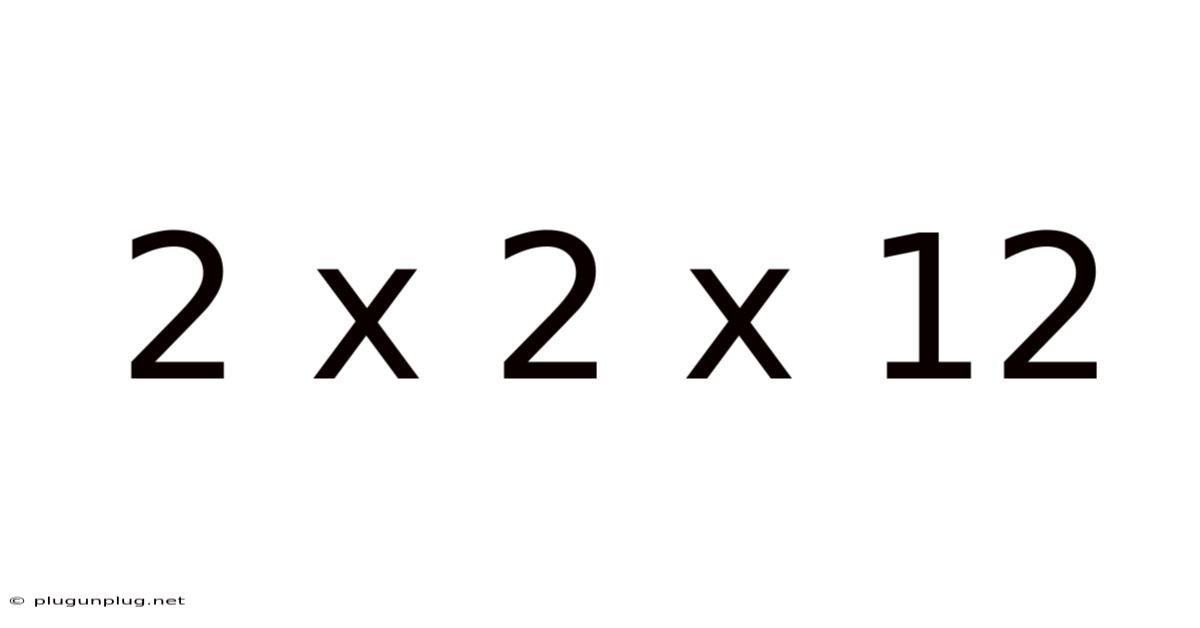
Table of Contents
Exploring the Mathematical Landscape of 2 x 2 x 12: From Simple Multiplication to Real-World Applications
This article delves into the seemingly simple mathematical expression "2 x 2 x 12," exploring its various interpretations, applications, and the broader mathematical concepts it represents. While the calculation itself is straightforward, its implications extend beyond a simple numerical answer, offering a gateway to understand fundamental principles in arithmetic, geometry, and even problem-solving strategies. We will unpack this seemingly simple equation, revealing its hidden depths and practical relevance.
Understanding the Basics: Multiplication and its Properties
Before diving into the specifics of 2 x 2 x 12, let's refresh our understanding of multiplication. Multiplication is essentially repeated addition. 2 x 2, for instance, means adding two '2s' together (2 + 2 = 4). Extending this to 2 x 2 x 12 means we are repeatedly adding groups of four, twelve times. This can be visualized in several ways:
- Repeated Addition: 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 48
- Repeated Multiplication: (2 x 2) x 12 = 4 x 12 = 48
- Associative Property: 2 x (2 x 12) = 2 x 24 = 48
The associative property of multiplication allows us to rearrange the order of operations without affecting the final result. This property is crucial in more complex calculations and demonstrates the flexibility of mathematical operations. Understanding these different approaches helps build a stronger intuition about multiplication and its properties.
Calculating 2 x 2 x 12: A Step-by-Step Approach
The calculation of 2 x 2 x 12 is quite straightforward. We can solve it in multiple ways:
Method 1: Left-to-Right Calculation
- First Multiplication: 2 x 2 = 4
- Second Multiplication: 4 x 12 = 48
Method 2: Associative Property Application
- Grouping: (2 x 12) x 2 = 24 x 2 = 48
- Alternative Grouping: 2 x (2 x 12) = 2 x 24 = 48
Both methods yield the same result: 48. This reinforces the associative property of multiplication, highlighting its usefulness in simplifying calculations.
Visualizing 2 x 2 x 12: A Geometric Perspective
Beyond simple arithmetic, we can visualize 2 x 2 x 12 geometrically. Imagine a rectangular prism (a box). The dimensions of this prism could be represented by our equation:
- Length: 2 units
- Width: 2 units
- Height: 12 units
The result, 48, represents the volume of this rectangular prism. This connection between arithmetic and geometry illustrates the interconnectedness of mathematical concepts. We can use this visualization to solve practical problems involving volume calculations. For instance, imagine calculating the volume of a storage container with these dimensions, or determining the amount of material needed to fill a box of these specifications.
Real-World Applications of 2 x 2 x 12
While seemingly simple, the expression "2 x 2 x 12" and its result, 48, has surprisingly diverse applications in various real-world scenarios:
- Packaging and Shipping: Imagine calculating the number of items in a box. If each layer contains 4 items (2 x 2), and there are 12 layers, the total number of items is 48.
- Construction and Engineering: Calculations involving volume, area, and quantity estimation in construction projects often involve similar multiplications. Imagine calculating the number of bricks needed to build a wall, where each layer has 4 bricks (2 x 2) and the wall has 12 layers.
- Inventory Management: Tracking the number of items in a warehouse or store might involve counting units organized in layers or stacks.
- Data Analysis: In data analysis, the expression could represent the total number of data points if you have 2 categories of data, 2 subcategories within each category, and 12 observations for each subcategory.
These examples demonstrate that seemingly simple mathematical concepts form the foundation for more complex real-world problems. The ability to efficiently and accurately solve basic mathematical expressions like 2 x 2 x 12 is fundamental to success in various fields.
Extending the Concept: Exploring Variations and Extensions
We can extend our understanding by considering variations and extensions of the 2 x 2 x 12 problem:
- Changing Dimensions: What if we altered the dimensions of our rectangular prism? How would the volume change if we increased the length to 3, the width to 3, and kept the height at 12? The volume would then be 3 x 3 x 12 = 108. This allows us to explore the relationship between dimensions and volume.
- Adding More Factors: What if we added another factor? 2 x 2 x 12 x 2 = 96. This introduces the concept of expanding the problem to encompass more variables.
- Using Different Numbers: Replacing the numbers 2, 2, and 12 with other numbers allows us to explore the effects of varying numerical inputs on the outcome. This practice enhances understanding of the broader mathematical concepts involved.
Beyond the Numbers: Developing Problem-Solving Skills
The seemingly simple equation, 2 x 2 x 12, provides more than just a numerical answer. It serves as a valuable tool for developing essential problem-solving skills:
- Breaking down Complex Problems: The ability to break down a complex problem into smaller, manageable steps is vital. This equation exemplifies this process: we break down the multiplication into smaller steps for easier calculation.
- Visualizing Problems: The geometrical interpretation provides a visual representation of the problem. Visualizing helps in understanding and solving complex problems.
- Applying Mathematical Concepts: This problem allows us to apply basic arithmetic and geometric concepts, reinforcing our understanding of these foundational elements of mathematics.
- Identifying Patterns and Relationships: By exploring variations of the problem, we can identify patterns and relationships between the input values and the resulting output. This cultivates analytical thinking.
These problem-solving skills are transferable to various aspects of life, making the seemingly mundane calculation of 2 x 2 x 12 a surprisingly valuable exercise.
Frequently Asked Questions (FAQ)
Q: What is the most efficient way to calculate 2 x 2 x 12?
A: While both methods presented earlier are efficient, performing the first multiplication (2 x 2 = 4) followed by the second (4 x 12 = 48) is often the most intuitive and straightforward approach for most individuals.
Q: Can I use a calculator to solve this problem?
A: Yes, certainly. Calculators are useful tools for solving mathematical problems, especially for more complex calculations. However, understanding the underlying principles and being able to perform the calculation manually is beneficial for building a strong mathematical foundation.
Q: Are there any real-world applications beyond those mentioned?
A: Yes! Many areas like finance, cooking (measuring ingredients), or even game development (calculating game statistics) involve similar types of calculations. The applications are incredibly diverse.
Q: Why is understanding the associative property important?
A: The associative property simplifies calculations and allows for flexible problem-solving. It demonstrates that the order of multiplication does not affect the final result, offering an essential concept in more advanced mathematical operations.
Conclusion: The Unfolding Significance of 2 x 2 x 12
The seemingly simple calculation of 2 x 2 x 12 offers a profound insight into the beauty and practicality of mathematics. It's not merely about arriving at the answer 48, but about understanding the underlying principles of multiplication, applying these principles to various contexts, and developing crucial problem-solving skills. From its geometric representation to its diverse real-world applications, this simple expression demonstrates the interconnectedness of mathematical concepts and their relevance in our daily lives. By exploring this seemingly basic equation, we’ve uncovered a wealth of mathematical understanding and valuable problem-solving strategies. The journey from a simple calculation to a comprehensive understanding of its implications highlights the richness and depth embedded within even the most fundamental mathematical concepts.
Latest Posts
Latest Posts
-
72 Degrees F In C
Sep 22, 2025
-
What Is A Kj Calorie
Sep 22, 2025
-
Official Language Spoken In Brazil
Sep 22, 2025
-
Greater Antilles In The Caribbean
Sep 22, 2025
-
How To Find Netflix Password
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.