3 4 X 3 5
plugunplug
Sep 17, 2025 · 6 min read
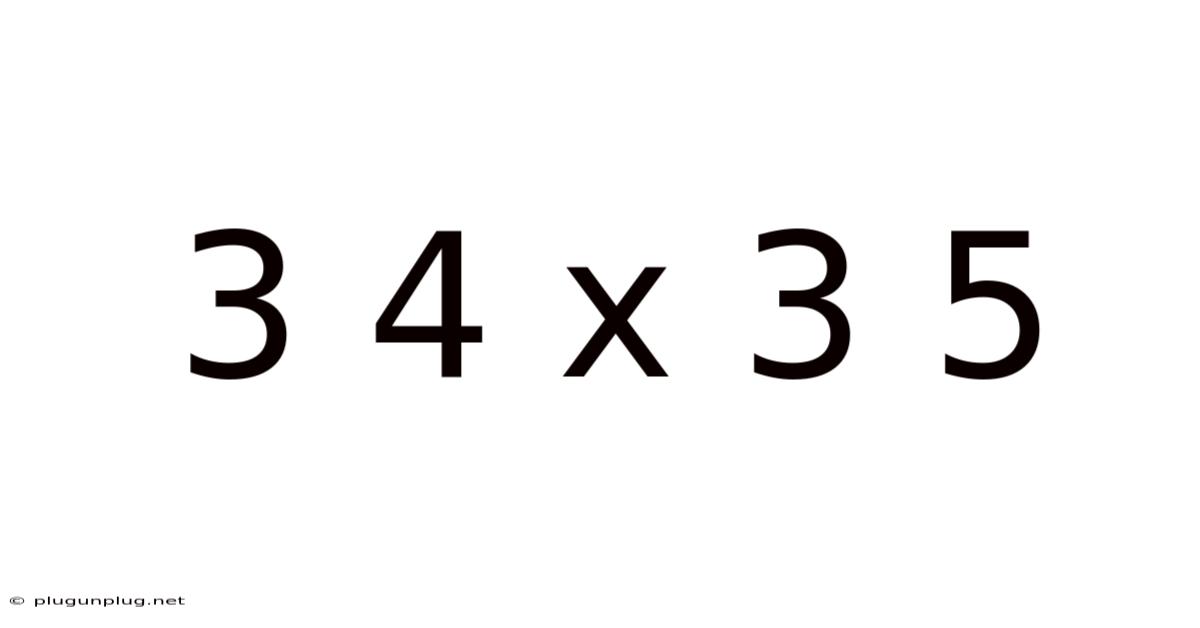
Table of Contents
Decoding 3/4 x 3/5: A Deep Dive into Fraction Multiplication
This article provides a comprehensive guide to understanding and solving fraction multiplication problems, specifically focusing on the example 3/4 x 3/5. We'll move beyond simply providing the answer to explore the underlying principles, different methods of solving the problem, and practical applications. Understanding fraction multiplication is a fundamental skill in mathematics, crucial for various fields from cooking and construction to advanced scientific calculations. We'll break down the process step-by-step, making it accessible to learners of all levels.
Understanding Fractions: A Quick Recap
Before tackling 3/4 x 3/5, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, the numerator 3 represents 3 parts, and the denominator 4 indicates that the whole is divided into 4 equal parts.
Key Terminology:
- Numerator: The top number of a fraction.
- Denominator: The bottom number of a fraction.
- Proper Fraction: A fraction where the numerator is less than the denominator (e.g., 3/4).
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator (e.g., 5/4).
- Mixed Number: A number consisting of a whole number and a proper fraction (e.g., 1 1/4).
Multiplying Fractions: The Straightforward Method
The simplest method for multiplying fractions is to multiply the numerators together and then multiply the denominators together. Let's apply this to our example, 3/4 x 3/5:
- Multiply the numerators: 3 x 3 = 9
- Multiply the denominators: 4 x 5 = 20
- Combine the results: The product is 9/20.
Therefore, 3/4 x 3/5 = 9/20. This fraction is already in its simplest form because the greatest common divisor (GCD) of 9 and 20 is 1. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1.
Visualizing Fraction Multiplication: The Area Model
Visualizing the multiplication can solidify your understanding. Imagine a rectangle with a width of 3/4 and a height of 3/5. The area of this rectangle represents the product of the two fractions.
- Represent 3/4: Divide the rectangle into 4 equal columns and shade 3 of them to represent 3/4.
- Represent 3/5: Now, divide the rectangle into 5 equal rows and shade 3 of them to represent 3/5.
- Identify the Overlap: The overlapping shaded area represents the product. Count the number of overlapping squares and compare it to the total number of squares in the rectangle. You'll find that 9 out of 20 squares are doubly shaded, representing the fraction 9/20.
Simplifying Fractions Before Multiplication: A More Efficient Approach
While the straightforward method is easy to understand, simplifying before multiplication can often make the calculation simpler. This involves canceling out common factors between the numerators and denominators. Let's re-examine 3/4 x 3/5 using this method:
- Identify Common Factors: In this case, there are no common factors between the numerators and denominators. Therefore, we proceed directly to multiplication as shown in the previous method.
However, let’s consider another example: (2/6) x (3/4). Here, we can simplify:
- Simplify the fractions: 2/6 simplifies to 1/3 (dividing both numerator and denominator by 2). 3/4 remains as it is.
- Multiply the simplified fractions: (1/3) x (3/4) = (1 x 3) / (3 x 4) = 3/12
- Further Simplify: 3/12 simplifies to 1/4 (dividing both numerator and denominator by 3).
This illustrates that simplifying before multiplication can lead to smaller numbers, making the calculation easier and reducing the need for simplification at the end.
Multiplying Fractions with Mixed Numbers
Sometimes, you'll encounter mixed numbers in fraction multiplication problems. To multiply fractions involving mixed numbers, you first convert the mixed numbers into improper fractions. Let's illustrate with an example:
1 ½ x 2/3
- Convert Mixed Number to Improper Fraction: 1 ½ = (1 x 2 + 1) / 2 = 3/2
- Multiply the Improper Fractions: (3/2) x (2/3) = (3 x 2) / (2 x 3) = 6/6
- Simplify: 6/6 simplifies to 1
Therefore, 1 ½ x 2/3 = 1.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it has numerous practical applications in everyday life:
- Cooking: Scaling recipes up or down requires multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you multiply 1/2 by 2, resulting in 1 cup of flour.
- Construction: Calculating material quantities, such as the amount of lumber needed for a project, often involves multiplying fractions.
- Sewing/Tailoring: Adjusting patterns or calculating fabric yardage requires fraction multiplication.
- Finance: Calculating percentages, discounts, and interest often involves fractions.
Advanced Concepts and Extensions
While the basic principles of fraction multiplication are relatively straightforward, understanding the underlying mathematical principles allows for further exploration of more complex topics such as:
- Multiplying more than two fractions: The same principles apply when multiplying three or more fractions. Simply multiply all numerators together and all denominators together. Simplification before multiplication is highly recommended to make the process more efficient.
- Fractions and exponents: Understanding how to multiply fractions forms the basis for understanding the behavior of fractions raised to powers.
- Algebraic fractions: The same rules apply when dealing with variables and algebraic expressions in the numerator and denominator.
Frequently Asked Questions (FAQ)
Q: What happens if I multiply a fraction by 1?
A: Multiplying a fraction by 1 results in the same fraction. This is because any number multiplied by 1 remains unchanged.
Q: Can I multiply fractions with different denominators directly?
A: Yes, you can directly multiply the numerators and denominators regardless of whether the denominators are the same or different.
Q: Why is simplifying before multiplication helpful?
A: Simplifying before multiplication reduces the size of the numbers you're working with, making the calculations easier and minimizing the chance of errors. It also leads to a simplified result, removing the need for further simplification at the end.
Q: What if the result is an improper fraction?
A: An improper fraction can be converted into a mixed number by dividing the numerator by the denominator. The quotient becomes the whole number part, and the remainder becomes the numerator of the fractional part.
Q: Are there any online tools or calculators to help with fraction multiplication?
A: While this article discourages external links, a quick online search for "fraction calculator" will provide numerous tools to assist you with fraction multiplication and other fraction-based calculations.
Conclusion
Mastering fraction multiplication is a crucial step in building a strong mathematical foundation. By understanding the underlying principles, visualizing the process, and practicing different methods, you can confidently tackle even more complex fraction problems. The examples and explanations provided in this article should equip you with the necessary tools to not only solve problems like 3/4 x 3/5 but also to apply these skills to real-world situations. Remember, practice makes perfect, so continue to work with fractions, and soon you'll find them as easy as working with whole numbers.
Latest Posts
Latest Posts
-
2 X 3 X 7
Sep 17, 2025
-
11 25 As A Decimal
Sep 17, 2025
-
What Did Isaac Newton Achieve
Sep 17, 2025
-
Why Do Organisms Need Energy
Sep 17, 2025
-
How To You Spell Supercalifragilisticexpialidocious
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 4 X 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.