3x X 2 X 2
plugunplug
Sep 24, 2025 · 6 min read
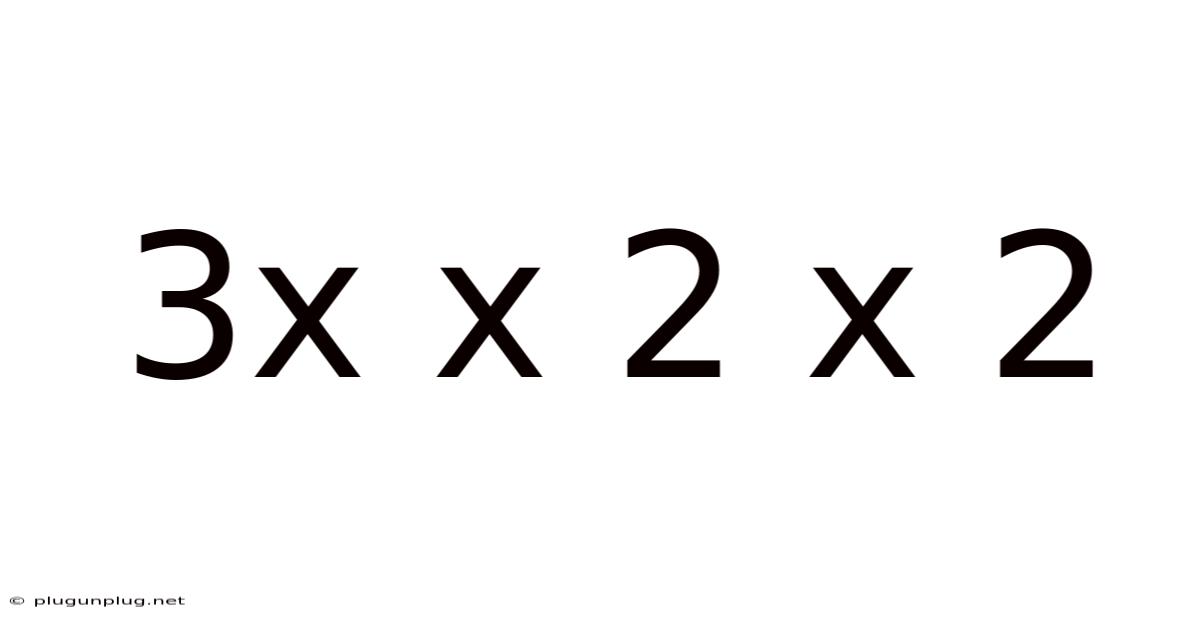
Table of Contents
Decoding 3 x 3 x 2 x 2: Exploring Multiplication, Factorization, and its Applications
This article delves into the seemingly simple mathematical expression "3 x 3 x 2 x 2," exploring its various interpretations, applications, and underlying mathematical concepts. We'll move beyond simply calculating the answer to understand the significance of this expression within broader mathematical frameworks, including multiplication, factorization, and its relevance in real-world scenarios. Understanding this seemingly basic equation unlocks a deeper appreciation for fundamental mathematical principles.
Understanding the Basics: Multiplication and its Properties
At its core, "3 x 3 x 2 x 2" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that involves repeated addition. For instance, 3 x 2 is the same as 2 + 2 + 2, or 3 added to itself twice. The expression "3 x 3 x 2 x 2" combines several multiplication operations. The order in which we perform these operations doesn't affect the final result due to the commutative and associative properties of multiplication. This means that 3 x 3 x 2 x 2 is equal to 2 x 2 x 3 x 3, or any other arrangement of these factors.
Calculating the Result: Step-by-Step Solution
Let's break down the calculation step-by-step:
-
3 x 3: This equals 9.
-
2 x 2: This equals 4.
-
9 x 4: Multiplying the results from steps 1 and 2 gives us 36.
Therefore, 3 x 3 x 2 x 2 = 36. This simple calculation forms the basis for understanding more complex mathematical concepts.
Factorization: Breaking Down the Number 36
The result of our calculation, 36, can be further explored through factorization. Factorization involves breaking down a number into its prime factors. Prime numbers are whole numbers greater than 1 that have only two divisors: 1 and themselves. The prime factorization of 36 is 2 x 2 x 3 x 3, which is directly represented in our original expression. Understanding the prime factorization of a number is crucial in various mathematical applications, including simplifying fractions, solving equations, and understanding number theory.
The prime factorization helps us understand the building blocks of the number 36. We can see that it's composed of two 2's and two 3's. This information is valuable when working with fractions, simplifying expressions, or exploring the properties of numbers.
Applications in Geometry and Measurement
The expression "3 x 3 x 2 x 2" frequently appears in geometrical calculations. Imagine a rectangular prism (a box) with dimensions 3 units by 3 units by 2 units. The volume of this prism would be calculated using the formula: length x width x height. In this case, the volume is 3 x 3 x 2 = 18 cubic units. If we had two such prisms, the total volume would be 18 x 2 = 36 cubic units, directly relating back to our original expression.
Applications in Algebra and Equations
In algebra, the expression can represent variables. For instance, if we let 'x' represent 3 and 'y' represent 2, then the expression becomes x * x * y * y, or x²y². This algebraic representation allows us to explore more complex equations and relationships. Solving equations involving variables and exponents is a fundamental skill in algebra and various scientific fields.
Applications in Combinatorics and Probability
The expression can also relate to combinatorial problems. Imagine choosing two items from a set of three distinct items (e.g., selecting two colors from a set of three). The number of ways to do this with replacement (meaning you can choose the same item twice) is 3 x 3 = 9. If we further extend this to selecting two items from another set of two distinct items, we would multiply the number of possibilities (9) by the possibilities in the second set (2 x 2 = 4), resulting in 36 possible combinations. This shows the relevance of this expression in areas like probability and statistics.
Expanding the Concept: Exponents and Powers
The expression "3 x 3 x 2 x 2" can be simplified using exponents. Exponents represent repeated multiplication of a base number. We can rewrite the expression as 3² x 2², indicating that 3 is multiplied by itself twice, and 2 is multiplied by itself twice. Understanding exponents is crucial for simplifying complex expressions and solving equations involving powers. Working with exponents simplifies calculations and leads to a better understanding of exponential growth and decay in various real-world phenomena.
Beyond Simple Multiplication: A Deeper Dive into Number Theory
The seemingly simple 3 x 3 x 2 x 2 opens the door to more advanced mathematical concepts within Number Theory.
-
Divisibility: Understanding the prime factorization (2² x 3²) allows us to quickly determine the divisors of 36. Any combination of the prime factors and their powers will be a divisor. For example, 2, 3, 4, 6, 9, 12, 18, and 36 are all divisors of 36. This is crucial for simplifying fractions, finding common denominators, and solving various mathematical problems.
-
Modular Arithmetic: In modular arithmetic, we consider the remainder after division by a specific number (the modulus). For example, 36 modulo 5 (written as 36 mod 5) equals 1, because 36 divided by 5 leaves a remainder of 1. Modular arithmetic is fundamental in cryptography, computer science, and various other fields.
-
Perfect Numbers: Although 36 isn't a perfect number (a number equal to the sum of its proper divisors), exploring this concept helps to understand the connections between numbers and their divisors. Perfect numbers, like 6 and 28, are fascinating objects of study in number theory.
-
Square Numbers: Notice that both 3 x 3 (9) and 2 x 2 (4) are square numbers (the result of squaring an integer). The number 36 itself is also a square number (6²). Recognizing patterns like this leads to a deeper understanding of number properties.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 3 x 3 x 2 x 2 and 3 x (3 x 2 x 2)?
- A: There's no difference in the final result. Due to the associative property of multiplication, the order of operations within parentheses does not change the outcome. Both expressions equal 36.
-
Q: How can I use this in real life?
- A: This concept is foundational for various real-life applications. It's useful for calculating areas and volumes (as discussed with the rectangular prism), determining the number of combinations, understanding proportions, and much more.
-
Q: Are there other ways to express 36 as a product of numbers?
- A: Yes, many ways exist. Some include: 6 x 6, 4 x 9, 12 x 3, 18 x 2, and others. However, 2 x 2 x 3 x 3 represents the unique prime factorization.
-
Q: What is the importance of understanding prime factorization?
- A: Prime factorization is a cornerstone of number theory and essential for simplifying fractions, finding greatest common divisors (GCD) and least common multiples (LCM), and solving various mathematical problems.
Conclusion: Beyond the Numbers
The expression "3 x 3 x 2 x 2," while seemingly straightforward, serves as a gateway to understanding fundamental mathematical principles. From simple multiplication and factorization to the deeper concepts of exponents, number theory, and real-world applications, this expression provides a solid foundation for mathematical exploration. The key is not just to calculate the answer (36), but to appreciate the underlying mathematical structures and their connections to various fields of study. By exploring these concepts, we unlock a richer understanding of the beauty and power of mathematics.
Latest Posts
Latest Posts
-
Specific Charge Of The Electron
Sep 25, 2025
-
Disadvantages Of Embryonic Stem Cells
Sep 25, 2025
-
How Do You Long Division
Sep 25, 2025
-
115 Degrees C To F
Sep 25, 2025
-
Why Did George Kill Lennie
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3x X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.