5 Out Of 15 Percentage
plugunplug
Sep 20, 2025 · 5 min read
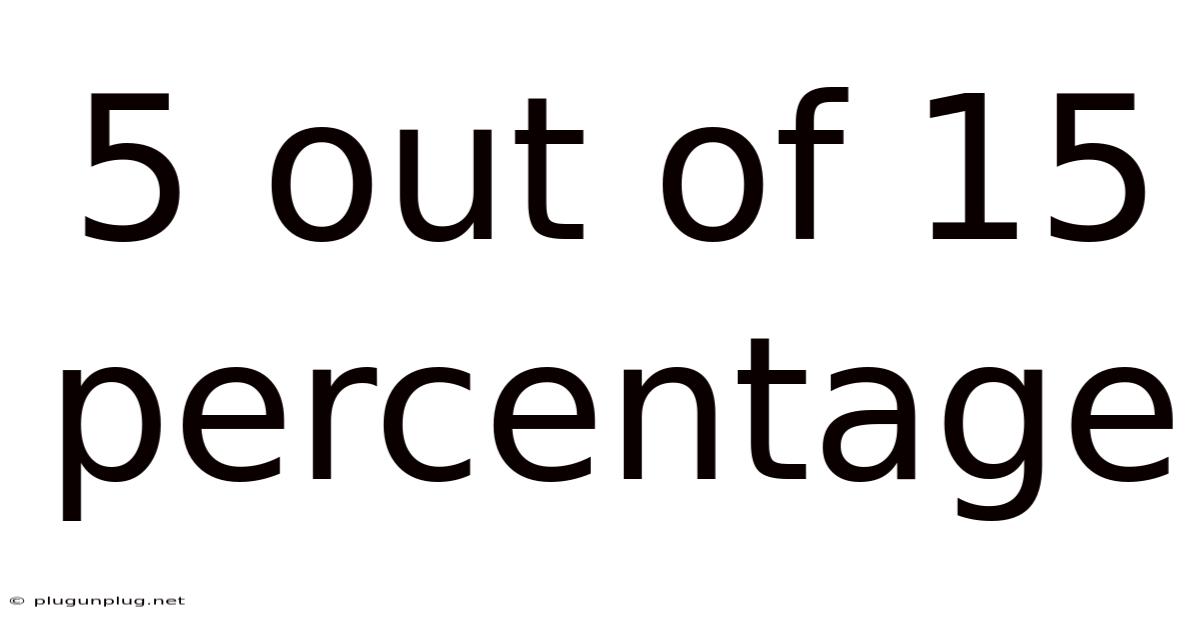
Table of Contents
Decoding 5 out of 15: Understanding Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in daily life, from calculating discounts and taxes to interpreting statistical data and understanding financial reports. This article delves into the meaning of "5 out of 15," explains how to calculate percentages, and explores various real-world scenarios where this type of calculation is crucial. We'll also address common misconceptions and offer practical tips for mastering percentage calculations.
What Does "5 out of 15" Mean?
"5 out of 15" represents a fraction where 5 is the numerator (the part) and 15 is the denominator (the whole). It signifies that 5 units are selected or present from a total of 15 units. This fraction can be expressed in various ways, all representing the same proportion:
- Fraction: 5/15
- Decimal: 0.333... (approximately 0.33)
- Percentage: 33.33% (approximately 33%)
Calculating Percentages: A Step-by-Step Guide
Calculating percentages involves converting a fraction into a percentage. Here's a straightforward method:
1. Convert the Fraction: Express the given information as a fraction. In our case, "5 out of 15" becomes 5/15.
2. Simplify the Fraction (Optional): Simplifying the fraction makes the calculation easier. We can divide both the numerator and the denominator by their greatest common divisor (GCD), which is 5 in this case:
5/15 = 1/3
3. Convert the Fraction to a Decimal: Divide the numerator by the denominator:
1 ÷ 3 ≈ 0.333...
4. Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the "%" symbol:
0.333... × 100 ≈ 33.33%
Real-World Applications of Percentage Calculations
The ability to calculate percentages is indispensable in various real-life situations. Here are some examples:
-
Academic Performance: Imagine a student scoring 5 out of 15 on a quiz. Understanding the percentage (33.33%) helps assess their performance relative to the total marks. This allows for a better understanding of their strengths and weaknesses and informs future study strategies.
-
Sales and Discounts: Stores often advertise discounts as percentages. For example, a 33.33% discount on a $30 item means a reduction of $10 ($30 x 0.3333 ≈ $10). Calculating the final price requires understanding percentage reductions.
-
Financial Literacy: Percentages are crucial for understanding interest rates, investment returns, and tax calculations. For instance, a 5% interest rate on a loan means that for every $100 borrowed, you'll pay $5 in interest annually.
-
Statistical Analysis: Percentages are widely used in statistics to represent proportions within a dataset. For example, if a survey shows that 5 out of 15 people prefer a particular brand, the percentage (33.33%) indicates the popularity of that brand among the surveyed group. This type of data is used extensively in market research, public opinion polls, and scientific studies.
-
Sports Statistics: In sports, percentages are used to express various performance metrics. For example, a basketball player's free-throw percentage is calculated by dividing the number of successful free throws by the total number of attempts. This metric helps evaluate a player's shooting accuracy and overall performance.
Beyond the Basics: Understanding Percentage Increase and Decrease
While the "5 out of 15" example focuses on calculating a percentage of a whole, it's equally important to understand percentage increase and decrease.
Percentage Increase: This calculates the percentage change when a value increases. The formula is:
[(New Value - Original Value) / Original Value] x 100%
Percentage Decrease: This calculates the percentage change when a value decreases. The formula is:
[(Original Value - New Value) / Original Value] x 100%
Common Misconceptions about Percentages
Several common misconceptions surround percentage calculations:
-
Adding Percentages Directly: You cannot simply add percentages directly unless they are based on the same whole. For instance, a 10% increase followed by a 10% decrease does not result in a net change of 0%.
-
Misinterpreting Percentage Points: A percentage point is a difference between two percentages, not a percentage change. For example, an increase from 10% to 20% is a 10-percentage-point increase, but a 100% percentage increase.
-
Ignoring the Base: Always clearly identify the base or whole when working with percentages. A 10% increase of 100 is different from a 10% increase of 1000.
Practical Tips for Mastering Percentage Calculations
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Solve various problems involving different scenarios.
-
Use Calculators Effectively: While mental calculation is valuable, using a calculator efficiently can save time and improve accuracy, especially with complex calculations.
-
Check Your Work: Always double-check your calculations to avoid errors. Ensure your answer makes sense within the context of the problem.
-
Visual Aids: Use diagrams or charts to visualize the problem. This can help you understand the relationships between different values and improve your comprehension.
-
Break Down Complex Problems: If a problem seems overwhelming, break it down into smaller, more manageable steps. This will make the calculation process less daunting.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage of a number?
A: To calculate the percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to find 30% of 200, you would calculate 200 * 0.30 = 60.
Q: What is the difference between a percentage and a proportion?
A: A proportion is the ratio of a part to a whole, often expressed as a fraction. A percentage is a specific type of proportion expressed as a fraction of 100.
Q: How can I improve my understanding of percentages?
A: Practice regularly with different types of percentage problems. Utilize online resources, textbooks, and practice worksheets to enhance your understanding. Focus on understanding the underlying concepts rather than just memorizing formulas.
Conclusion
Understanding "5 out of 15" and, more broadly, percentage calculations is a crucial life skill. From managing finances to interpreting data, the ability to work with percentages is essential in navigating the complexities of the modern world. By mastering these concepts and applying the strategies outlined in this article, you'll gain a stronger foundation in mathematics and improve your ability to solve real-world problems involving proportions and percentages. Remember to practice regularly, break down complex problems into smaller steps, and always double-check your work to ensure accuracy. With dedicated effort, mastering percentages will become second nature.
Latest Posts
Latest Posts
-
Layers Of Atmosphere In Order
Sep 20, 2025
-
How To Add Mixed Numbers
Sep 20, 2025
-
Action Potential Absolute Refractory Period
Sep 20, 2025
-
Lytic Cycle Vs Lysogenic Cycle
Sep 20, 2025
-
Kilos To Stone Conversion Uk
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 15 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.