7 Out Of 20 Percentage
plugunplug
Sep 24, 2025 · 5 min read
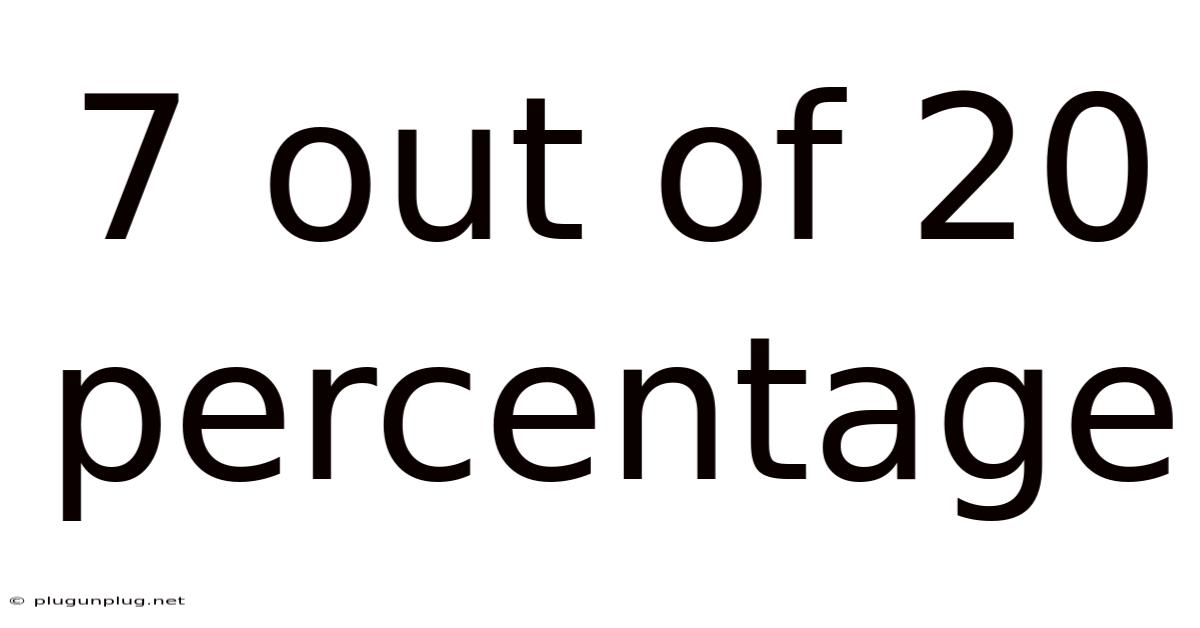
Table of Contents
Understanding 7 out of 20: A Comprehensive Guide to Percentages and Proportions
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts in a store to interpreting statistical data in research papers. This article delves deep into the seemingly simple concept of "7 out of 20," explaining not only how to calculate its percentage equivalent but also exploring the underlying mathematical principles and offering practical applications. We'll cover various methods of calculation, address common misconceptions, and provide examples to solidify your understanding. This comprehensive guide aims to empower you with a thorough grasp of percentages and their significance in everyday life.
What does "7 out of 20" Mean?
The phrase "7 out of 20" represents a ratio or fraction. It signifies that out of a total of 20 items or units, 7 possess a specific characteristic or belong to a particular group. To understand this better, imagine a class of 20 students, where 7 students received an A grade on a test. "7 out of 20" accurately describes this scenario.
Calculating the Percentage: Step-by-Step Guide
Converting a ratio or fraction like "7 out of 20" into a percentage involves a straightforward calculation:
Step 1: Express the ratio as a fraction:
The ratio "7 out of 20" can be written as the fraction 7/20.
Step 2: Convert the fraction to a decimal:
To convert the fraction to a decimal, divide the numerator (7) by the denominator (20):
7 ÷ 20 = 0.35
Step 3: Convert the decimal to a percentage:
Multiply the decimal by 100 and add the percentage symbol (%):
0.35 x 100 = 35%
Therefore, 7 out of 20 is equal to 35%.
Alternative Methods of Calculation
While the above method is the most common and straightforward, there are alternative approaches to arrive at the same result:
Method 1: Using Proportions:
You can set up a proportion to solve for the percentage:
7/20 = x/100
Cross-multiply:
20x = 700
Solve for x:
x = 700 ÷ 20 = 35
Therefore, x = 35%, confirming our earlier calculation.
Method 2: Using a Calculator:
Most calculators have a percentage function. Simply enter 7 ÷ 20 and then multiply by 100 to get the percentage directly.
Understanding Proportions and Ratios
The concept of "7 out of 20" is fundamentally rooted in the understanding of ratios and proportions. A ratio is a comparison of two quantities. In our case, the ratio is 7:20 (7 to 20). A proportion is a statement that two ratios are equal. We used a proportion in one of the alternative calculation methods above. Understanding these concepts is crucial for solving various percentage problems.
Practical Applications of Percentages
The ability to calculate percentages and understand ratios has numerous real-world applications:
-
Academic Performance: Calculating grades, understanding class rankings, and analyzing test scores. For example, if you answered 7 out of 20 questions correctly on a test, your score is 35%.
-
Financial Literacy: Calculating discounts, interest rates, taxes, tips, and investment returns. A 35% discount on a $100 item means you save $35.
-
Data Analysis: Interpreting statistical data, analyzing surveys, and understanding research findings. For instance, if 7 out of 20 respondents preferred a particular product, the preference rate is 35%.
-
Everyday Life: Dividing tasks, sharing resources, and understanding probabilities. If 7 out of 20 days are sunny, then the probability of a sunny day is 35%.
Common Misconceptions about Percentages
Several misconceptions often arise when dealing with percentages:
-
Confusion between percentage and absolute numbers: It's important to differentiate between the percentage (35%) and the absolute number (7). While 35% represents the proportion, 7 represents the actual quantity.
-
Incorrect addition or subtraction of percentages: Percentages cannot be directly added or subtracted unless they refer to the same base value. For example, a 10% discount followed by a 20% discount is not a 30% discount.
-
Misinterpreting percentage changes: Percentage changes should always be calculated relative to the original value. A 10% increase followed by a 10% decrease does not result in the original value.
Advanced Concepts and Extensions
Understanding "7 out of 20" lays the groundwork for more complex percentage calculations. Here are some extensions:
-
Calculating percentage increase or decrease: If the number of students who received an A grade increased from 7 to 10 out of 20, the percentage increase can be calculated.
-
Working with multiple percentages: Combining or comparing percentages from different data sets.
-
Understanding compound percentages: Calculating the effect of multiple percentage changes applied sequentially.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage if I have more than 20 items?
A: The same principle applies. Simply replace 20 with the total number of items, and 7 with the number of items you are interested in. Then, follow the steps outlined earlier.
Q: Can I use a different method to calculate percentages besides division and multiplication?
A: Yes, you can use proportions or a calculator with a percentage function, as explained earlier.
Q: What if I have a decimal number instead of a whole number?
A: The same process applies. You can use fractions, decimals, or a calculator to obtain the percentage.
Q: How do I convert a percentage back into a fraction or ratio?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the fraction. For example, 35% becomes 35/100, which simplifies to 7/20.
Conclusion
Understanding the concept of "7 out of 20" and its equivalent percentage of 35% is not merely about performing a simple calculation. It’s about grasping the fundamental principles of ratios, proportions, and percentages, which are essential tools in various fields and everyday life. This article aimed to provide a comprehensive understanding, moving beyond the basic calculation to cover various methods, applications, and potential misconceptions. By mastering these concepts, you equip yourself with a valuable skillset applicable far beyond the simple calculation of 7 out of 20. Remember to practice regularly to solidify your understanding and build confidence in handling percentages effectively.
Latest Posts
Latest Posts
-
How Far Is 1 5 Kilometers
Sep 24, 2025
-
3 6kg To Lbs And Oz
Sep 24, 2025
-
Convert Kilometers To Miles Formula
Sep 24, 2025
-
Height X Width X Depth
Sep 24, 2025
-
Great Britain Size Square Miles
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 20 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.