Double Angle Formula Cos 2x
plugunplug
Sep 22, 2025 · 6 min read
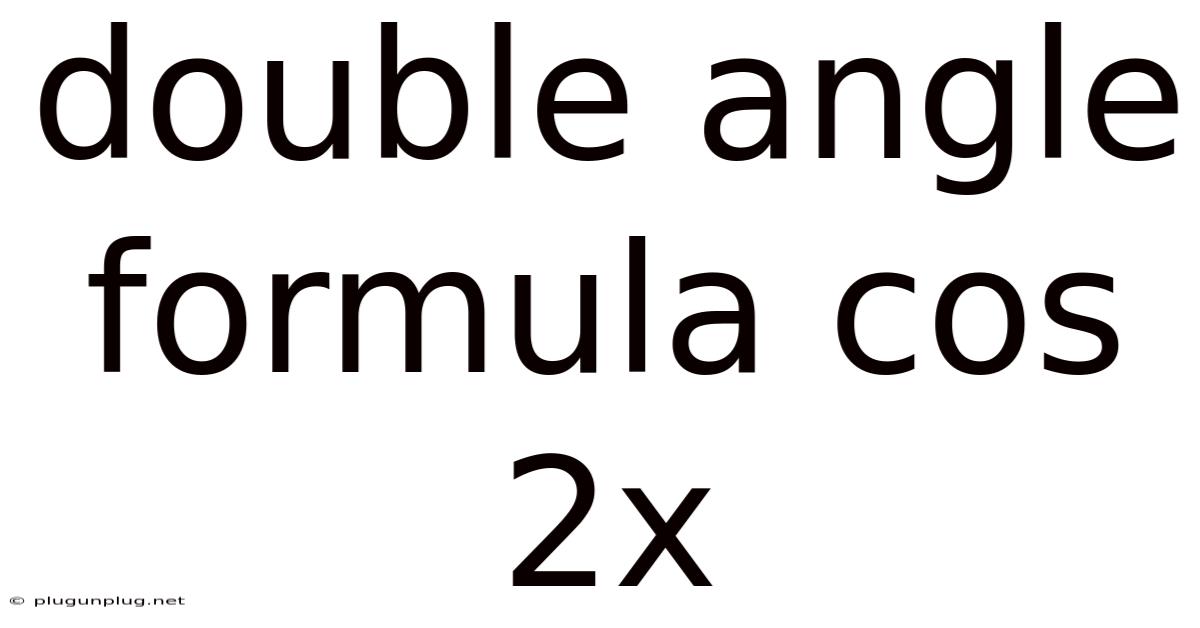
Table of Contents
Mastering the Double Angle Formula for Cos 2x: A Comprehensive Guide
The double angle formula for cosine, specifically cos 2x, is a fundamental concept in trigonometry with wide-ranging applications in calculus, physics, and engineering. Understanding this formula and its various forms is crucial for solving complex trigonometric equations and simplifying intricate expressions. This comprehensive guide will delve deep into the derivation, different forms, applications, and common misconceptions surrounding the cos 2x formula, ensuring a thorough understanding for learners of all levels.
Introduction: Unveiling the Cos 2x Formula
The double angle formula for cosine, cos 2x, expresses the cosine of twice an angle (2x) in terms of trigonometric functions of the original angle (x). This formula is derived from the angle sum formula for cosine, which states: cos(A + B) = cos A cos B - sin A sin B. By setting A = x and B = x, we directly obtain the primary form of the double angle formula. This seemingly simple formula opens the door to a wealth of problem-solving techniques and deeper mathematical insights. Mastering cos 2x is key to unlocking more advanced trigonometric concepts and their applications in various fields.
Derivation of the Cos 2x Formula from the Angle Sum Formula
Let's derive the cos 2x formula step-by-step using the angle sum formula:
-
Start with the angle sum formula: cos(A + B) = cos A cos B - sin A sin B
-
Substitute A = x and B = x: cos(x + x) = cos x cos x - sin x sin x
-
Simplify: cos 2x = cos²x - sin²x
This is the fundamental form of the double angle formula for cosine. However, we can further manipulate this expression to obtain alternative, equally useful forms.
Three Key Forms of the Cos 2x Formula
While cos 2x = cos²x - sin²x is the foundational form, we can derive two other equally important forms using fundamental trigonometric identities:
-
Form 1: cos 2x = cos²x - sin²x (The fundamental form, derived directly from the angle sum formula.)
-
Form 2: cos 2x = 2cos²x - 1 (Derived using the Pythagorean identity sin²x + cos²x = 1, substituting sin²x = 1 - cos²x into Form 1.)
-
Form 3: cos 2x = 1 - 2sin²x (Derived similarly, substituting cos²x = 1 - sin²x into Form 1.)
Each of these forms has its own advantages, depending on the context of the problem. Knowing when to use each form is crucial for efficient problem-solving.
Applications of the Cos 2x Formula
The cos 2x formula has numerous applications across various mathematical and scientific disciplines. Some key applications include:
-
Solving Trigonometric Equations: The cos 2x formula is invaluable in simplifying and solving complex trigonometric equations. By substituting cos 2x with its equivalent forms, we can often reduce the equation's complexity and find solutions more easily. For example, an equation like 2cos²x - 1 = ½ can be simplified using Form 2 to solve for x.
-
Trigonometric Identities and Simplification: This formula plays a vital role in simplifying complex trigonometric expressions and proving other trigonometric identities. By substituting appropriate forms of cos 2x, we can often reduce lengthy expressions into simpler, more manageable forms.
-
Calculus: The cos 2x formula is crucial in integration and differentiation involving trigonometric functions. For instance, integrating expressions containing cos²x often involves using Form 2 to rewrite the expression in a more integrable form.
-
Physics and Engineering: Many physical phenomena, such as oscillations and waves, are modeled using trigonometric functions. The double angle formula is essential in analyzing these models and solving related problems. For example, in the study of simple harmonic motion, the cosine function appears prominently, and using the double angle formula allows for simplification and deeper analysis of the motion.
-
Geometry: The cosine rule in trigonometry often leads to expressions involving cos 2x, enabling the calculation of unknown angles or sides in various geometric problems.
Step-by-Step Examples: Solving Problems with Cos 2x
Let's work through some examples to illustrate the practical application of the cos 2x formula:
Example 1: Solving a Trigonometric Equation
Solve the equation: cos 2x = ½ for 0 ≤ x ≤ 2π
Solution:
Using the definition of cos 2x directly isn't the most efficient approach. We can rewrite the equation as:
cos 2x = ½
Now we solve for 2x:
2x = π/3 + 2kπ or 2x = 5π/3 + 2kπ, where k is an integer.
Dividing by 2, we get:
x = π/6 + kπ or x = 5π/6 + kπ
For 0 ≤ x ≤ 2π, the solutions are: x = π/6, 5π/6, 7π/6, 11π/6.
Example 2: Simplifying a Trigonometric Expression
Simplify the expression: cos⁴x - sin⁴x
Solution:
We can factor this expression as a difference of squares:
cos⁴x - sin⁴x = (cos²x - sin²x)(cos²x + sin²x)
Since cos²x + sin²x = 1 (Pythagorean identity), the expression simplifies to:
cos⁴x - sin⁴x = cos²x - sin²x
Now, recognizing this as Form 1 of the cos 2x formula, we get:
cos⁴x - sin⁴x = cos 2x
Common Mistakes and Misconceptions
-
Confusing the Forms: Students often confuse the different forms of the cos 2x formula. It's crucial to understand the derivations and choose the appropriate form based on the given problem.
-
Incorrect Application of Identities: Improper application of Pythagorean identities or other trigonometric identities can lead to errors in simplifying expressions or solving equations. Careful attention to detail is necessary.
-
Forgetting the General Solution: When solving trigonometric equations involving cos 2x, it is crucial to remember the general solution, considering all possible values of x within a given range.
-
Ignoring the Domain and Range: Always consider the domain and range of the trigonometric functions involved when working with the cos 2x formula to avoid errors in calculations and interpretations.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between cos 2x and 2cos x?
- A: cos 2x is the cosine of twice an angle, while 2cos x is twice the cosine of an angle. They are distinct and not interchangeable.
-
Q: Can I use the cos 2x formula for any angle x?
- A: Yes, the cos 2x formula is valid for all real numbers x (angles in radians).
-
Q: How do I choose the best form of the cos 2x formula for a problem?
- A: The best form depends on the context. If the expression already contains sin²x, use Form 3; if it contains cos²x, use Form 2. If neither is prominent, use the fundamental Form 1.
-
Q: Are there other double angle formulas?
- A: Yes, there are also double angle formulas for sine (sin 2x = 2sin x cos x) and tangent (tan 2x = (2tan x) / (1 - tan²x)).
Conclusion: Mastering a Fundamental Trigonometric Tool
The double angle formula for cos 2x is a cornerstone of trigonometry and its applications extend far beyond the realm of pure mathematics. Understanding its derivation, various forms, and applications is essential for success in advanced mathematics, physics, engineering, and other related fields. By mastering this fundamental concept and practicing its applications, you'll build a strong foundation for tackling more complex trigonometric problems and unlocking deeper insights into the world of mathematics and its applications. Remember to practice regularly and pay close attention to detail, and you will become proficient in utilizing this powerful tool.
Latest Posts
Latest Posts
-
Which Organ System Produces Hormones
Sep 22, 2025
-
How To Pronounce Blue Curacao
Sep 22, 2025
-
Definition Of A Condensation Reaction
Sep 22, 2025
-
Secondary Effects Of An Earthquake
Sep 22, 2025
-
Ln 1 X Taylor Series
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Double Angle Formula Cos 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.