Is 121 A Square Number
plugunplug
Sep 22, 2025 · 6 min read
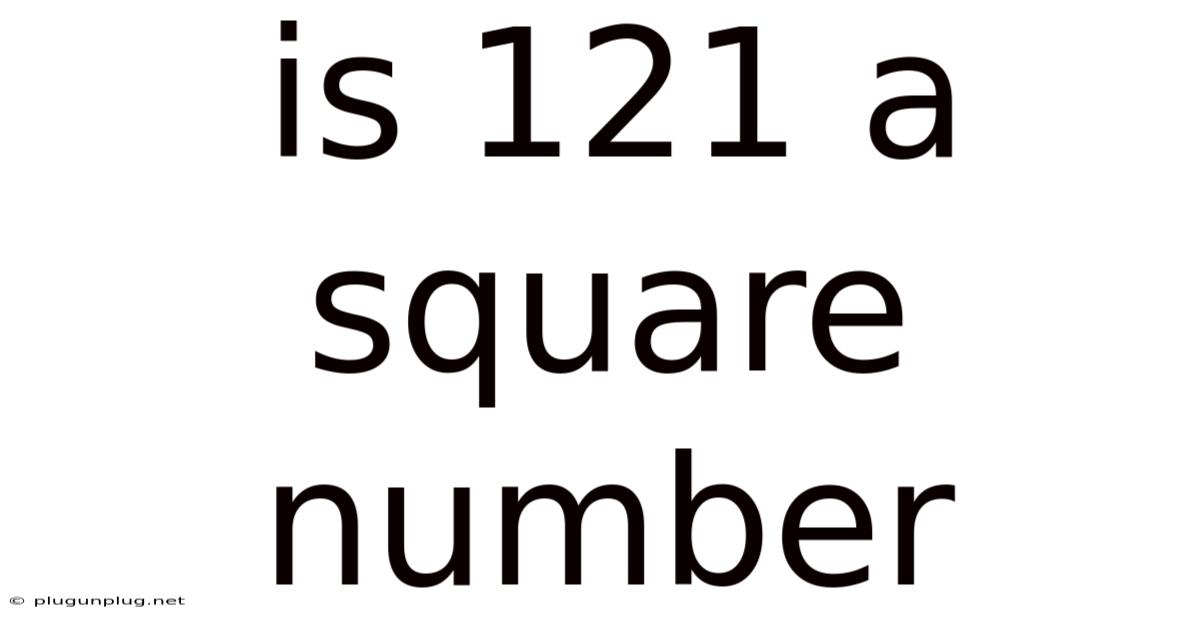
Table of Contents
Is 121 a Square Number? A Deep Dive into Square Roots and Perfect Squares
Is 121 a square number? The short answer is a resounding yes. But understanding why 121 is a square number opens up a fascinating world of mathematical concepts, including perfect squares, square roots, and their applications in various fields. This article will not only answer the initial question definitively but also explore the underlying principles and provide a comprehensive understanding of square numbers. We'll delve into the history, explore practical applications, and address frequently asked questions, making this a definitive guide to the intriguing world of perfect squares.
Understanding Square Numbers and Perfect Squares
Before we confirm whether 121 is a square number, let's establish a clear understanding of what constitutes a square number, often called a perfect square. A perfect square is a number that can be obtained by squaring (multiplying by itself) an integer. In other words, it's the result of multiplying a whole number by itself.
For example:
- 1 x 1 = 1 (1 is a perfect square)
- 2 x 2 = 4 (4 is a perfect square)
- 3 x 3 = 9 (9 is a perfect square)
- 4 x 4 = 16 (16 is a perfect square)
- And so on...
The sequence of perfect squares continues infinitely: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, and so forth. Each number in this sequence represents the area of a square with sides of integer length. This geometric interpretation is where the term "square number" originates.
Determining if 121 is a Square Number
Now, let's address the main question: Is 121 a square number? To determine this, we need to find out if there's an integer that, when multiplied by itself, equals 121. We can approach this in a few ways:
-
Trial and Error: We can start testing integers. We know 10 x 10 = 100, which is less than 121. Let's try 11: 11 x 11 = 121. Therefore, we've found our answer. 121 is a perfect square because it's the square of 11.
-
Square Root Calculation: The most efficient method is to find the square root of 121. The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, we represent this as √121. Using a calculator or applying mathematical methods, we find that √121 = 11. Since 11 is an integer, 121 is indeed a perfect square.
The Concept of Square Roots
The square root (√) is a fundamental concept in mathematics. It's the inverse operation of squaring. If a² = b, then a is the square root of b (√b = a). It's important to note that every positive number has two square roots: a positive and a negative one. For example, the square roots of 16 are +4 and -4 because both 4 x 4 = 16 and -4 x -4 = 16. However, when we talk about the square root of a number without specifying positive or negative, we usually refer to the principal square root, which is the positive one.
Practical Applications of Square Numbers and Square Roots
The concepts of square numbers and square roots are not merely abstract mathematical ideas; they have numerous practical applications across various fields:
-
Geometry: As mentioned earlier, perfect squares represent the area of squares with integer side lengths. This is fundamental in calculating areas, volumes, and other geometric properties. Understanding square roots allows us to find the side length of a square given its area.
-
Physics: Many physics formulas involve squares and square roots. For instance, calculating the distance an object falls under gravity, or determining the velocity of an object, often utilizes these concepts.
-
Engineering: Engineers use square roots and squares in structural calculations, determining the strength of materials, and designing various systems.
-
Computer Science: Square roots and squares are integral to many algorithms and computations in computer graphics, game development, and other areas of computer science.
-
Everyday Life: While less obvious, square roots and squares appear in everyday calculations, such as determining the diagonal length of a rectangular room or calculating the area of a floor.
Understanding Perfect Squares Beyond 121
While 121 is a perfect square, it's just one example within an infinite sequence. Understanding the patterns and properties of perfect squares helps in various mathematical calculations and problem-solving. Let's explore some properties:
-
Difference between consecutive squares: The difference between consecutive perfect squares increases by 2 each time. For instance:
- 4 - 1 = 3
- 9 - 4 = 5
- 16 - 9 = 7
- 25 - 16 = 9 ...and so on. This pattern continues indefinitely.
-
Sum of consecutive odd numbers: Each perfect square can be represented as the sum of consecutive odd numbers. For example:
- 1 = 1
- 4 = 1 + 3
- 9 = 1 + 3 + 5
- 16 = 1 + 3 + 5 + 7
- 25 = 1 + 3 + 5 + 7 + 9 This pattern is directly related to the visual representation of squares built from smaller squares.
Advanced Concepts Related to Square Numbers
Delving deeper, we encounter more sophisticated concepts related to square numbers:
-
Pythagorean Theorem: This fundamental theorem of geometry relates the squares of the sides of a right-angled triangle. It states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (a² + b² = c²). This theorem has countless applications in various fields, including surveying, navigation, and construction.
-
Diophantine Equations: These are equations where only integer solutions are sought. Many Diophantine equations involve squares and square roots, often leading to complex mathematical problems.
-
Number Theory: Square numbers play a significant role in number theory, a branch of mathematics that deals with the properties of integers. Many theorems and conjectures in number theory relate to the behavior and distribution of perfect squares.
Frequently Asked Questions (FAQ)
Q: How can I quickly determine if a large number is a perfect square?
A: For larger numbers, trial and error is inefficient. Using a calculator to find the square root is the quickest method. If the square root is an integer, the number is a perfect square.
Q: Are there any tricks to recognizing perfect squares?
A: While there isn't a foolproof trick, observing the last digit can sometimes help. Perfect squares can only end in 0, 1, 4, 5, 6, or 9. However, this is not sufficient to definitively determine if a number is a perfect square.
Q: What if the square root is not an integer?
A: If the square root of a number is not an integer, then the number is not a perfect square. It's simply a non-perfect square.
Q: Are there any negative perfect squares?
A: No, perfect squares are always non-negative because the square of any real number (positive or negative) is always non-negative.
Conclusion
In conclusion, 121 is definitively a square number because it's the square of 11 (11 x 11 = 121). This seemingly simple question opens the door to a rich understanding of square numbers, square roots, and their multifaceted applications in mathematics, science, and engineering. Understanding these concepts is crucial for various mathematical operations, problem-solving, and navigating diverse fields of study. Beyond the simple calculation, exploring the deeper meaning and applications of perfect squares enhances our mathematical literacy and problem-solving capabilities. The seemingly simple question, "Is 121 a square number?" thus unveils a world of mathematical richness and practical relevance.
Latest Posts
Latest Posts
-
Square Root Of 50 Simplified
Sep 22, 2025
-
3 Over 4 As Decimal
Sep 22, 2025
-
What Chromosomes Are Made Of
Sep 22, 2025
-
Function Of The Upper Epidermis
Sep 22, 2025
-
Weight In Kilos From Stones
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 121 A Square Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.